1. What is the difference between a relation and a function?
2. What is the difference between the input and the output of a function?
3. Why does the vertical line test tell us whether the graph of a relation represents a function?
4. How can you determine if a relation is a one-to-one function?
5. Why does the horizontal line test tell us whether the graph of a function is one-to-one?
For the following exercises, determine whether the relation represents a function.
6. [latex]\left\{\left(a,b\right),\text{ }\left(c,d\right),\text{ }\left(a,c\right)\right\}[/latex]
7. [latex]\left\{\left(a,b\right),\left(b,c\right),\left(c,c\right)\right\}[/latex]
For the following exercises, determine whether the relation represents [latex]y[/latex] as a function of [latex]x[/latex].
8. [latex]5x+2y=10[/latex]
9. [latex]y={x}^{2}[/latex]
10. [latex]x={y}^{2}[/latex]
11. [latex]3{x}^{2}+y=14[/latex]
12. [latex]2x+{y}^{2}=6[/latex]
13. [latex]y=-2{x}^{2}+40x[/latex]
14. [latex]y=\frac{1}{x}[/latex]
15. [latex]x=\frac{3y+5}{7y - 1}[/latex]
16. [latex]x=\sqrt{1-{y}^{2}}[/latex]
17. [latex]y=\frac{3x+5}{7x - 1}[/latex]
18. [latex]{x}^{2}+{y}^{2}=9[/latex]
19. [latex]2xy=1[/latex]
20. [latex]x={y}^{3}[/latex]
21. [latex]y={x}^{3}[/latex]
22. [latex]y=\sqrt{1-{x}^{2}}[/latex]
23. [latex]x=\pm \sqrt{1-y}[/latex]
24. [latex]y=\pm \sqrt{1-x}[/latex]
25. [latex]{y}^{2}={x}^{2}[/latex]
26. [latex]{y}^{3}={x}^{2}[/latex]
For the following exercises, evaluate the function [latex]f[/latex] at the indicated values [latex]\text{ }f\left(-3\right),f\left(2\right),f\left(-a\right),-f\left(a\right),f\left(a+h\right)[/latex].
27. [latex]f\left(x\right)=2x - 5[/latex]
28. [latex]f\left(x\right)=-5{x}^{2}+2x - 1[/latex]
29. [latex]f\left(x\right)=\sqrt{2-x}+5[/latex]
30. [latex]f\left(x\right)=\frac{6x - 1}{5x+2}[/latex]
31. [latex]f\left(x\right)=|x - 1|-|x+1|[/latex]
32. Given the function [latex]g\left(x\right)=5-{x}^{2}[/latex], evaluate [latex]\frac{g\left(x+h\right)-g\left(x\right)}{h},h\ne 0[/latex].
33. Given the function [latex]g\left(x\right)={x}^{2}+2x[/latex], evaluate [latex]\frac{g\left(x\right)-g\left(a\right)}{x-a},x\ne a[/latex].
34. Given the function [latex]k\left(t\right)=2t - 1:[/latex]
a. Evaluate [latex]k\left(2\right)[/latex].
b. Solve [latex]k\left(t\right)=7[/latex].
35. Given the function [latex]f\left(x\right)=8 - 3x:[/latex]
a. Evaluate [latex]f\left(-2\right)[/latex].
b. Solve [latex]f\left(x\right)=-1[/latex].
36. Given the function [latex]p\left(c\right)={c}^{2}+c:[/latex]
a. Evaluate [latex]p\left(-3\right)[/latex].
b. Solve [latex]p\left(c\right)=2[/latex].
37. Given the function [latex]f\left(x\right)={x}^{2}-3x:[/latex]
a. Evaluate [latex]f\left(5\right)[/latex].
b. Solve [latex]f\left(x\right)=4[/latex].
38. Given the function [latex]f\left(x\right)=\sqrt{x+2}:[/latex]
a. Evaluate [latex]f\left(7\right)[/latex].
b. Solve [latex]f\left(x\right)=4[/latex].
39. Consider the relationship [latex]3r+2t=18[/latex].
a. Write the relationship as a function [latex]r=f\left(t\right)[/latex].
b. Evaluate [latex]f\left(-3\right)[/latex].
c. Solve [latex]f\left(t\right)=2[/latex].
For the following exercises, use the vertical line test to determine which graphs show relations that are functions.
40.

41.

42.

43.

44.

45.

46.

47.

48.

49.

50.

51.

52. Given the following graph,
a. Evaluate [latex]f\left(-1\right)[/latex].
b. Solve for [latex]f\left(x\right)=3[/latex].

53. Given the following graph,
a. Evaluate [latex]f\left(0\right)[/latex].
b. Solve for [latex]f\left(x\right)=-3[/latex].

54. Given the following graph,
a. Evaluate [latex]f\left(4\right)[/latex].
b. Solve for [latex]f\left(x\right)=1[/latex].

For the following exercises, determine if the given graph is a one-to-one function.
55.

56.

57.

58.
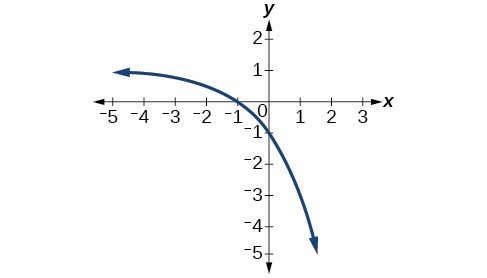
59.

For the following exercises, determine whether the relation represents a function.
60. [latex]\left\{\left(-1,-1\right),\left(-2,-2\right),\left(-3,-3\right)\right\}[/latex]
61. [latex]\left\{\left(3,4\right),\left(4,5\right),\left(5,6\right)\right\}[/latex]
62. [latex]\left\{\left(2,5\right),\left(7,11\right),\left(15,8\right),\left(7,9\right)\right\}[/latex]
For the following exercises, determine if the relation represented in table form represents [latex]y[/latex] as a function of [latex]x[/latex].
63.
| [latex]x[/latex] | 5 | 10 | 15 |
| [latex]y[/latex] | 3 | 8 | 14 |
64.
| [latex]x[/latex] | 5 | 10 | 15 |
| [latex]y[/latex] | 3 | 8 | 8 |
65.
| [latex]x[/latex] | 5 | 10 | 10 |
| [latex]y[/latex] | 3 | 8 | 14 |
For the following exercises, use the function [latex]f[/latex] represented in the table below.
| [latex]x[/latex] | [latex]f\left(x\right)[/latex] |
| 0 | 74 |
| 1 | 28 |
| 2 | 1 |
| 3 | 53 |
| 4 | 56 |
| 5 | 3 |
| 6 | 36 |
| 7 | 45 |
| 8 | 14 |
| 9 | 47 |
66. Evaluate [latex]f\left(3\right)[/latex].
67. Solve [latex]f\left(x\right)=1[/latex].
For the following exercises, evaluate the function [latex]f[/latex] at the values [latex]f\left(-2\right),f\left(-1\right),f\left(0\right),f\left(1\right)[/latex], and [latex]f\left(2\right)[/latex].
68. [latex]f\left(x\right)=4 - 2x[/latex]
69. [latex]f\left(x\right)=8 - 3x[/latex]
70. [latex]f\left(x\right)=8{x}^{2}-7x+3[/latex]
71. [latex]f\left(x\right)=3+\sqrt{x+3}[/latex]
72. [latex]f\left(x\right)=\frac{x - 2}{x+3}[/latex]
73. [latex]f\left(x\right)={3}^{x}[/latex]
For the following exercises, evaluate the expressions, given functions [latex]f,g[/latex], and [latex]h:[/latex]
- [latex]f\left(x\right)=3x - 2[/latex]
- [latex]g\left(x\right)=5-{x}^{2}[/latex]
- [latex]h\left(x\right)=-2{x}^{2}+3x - 1[/latex]
74. [latex]3f\left(1\right)-4g\left(-2\right)[/latex]
75. [latex]f\left(\frac{7}{3}\right)-h\left(-2\right)[/latex]
Applications
76. The amount of garbage, [latex]G[/latex], produced by a city with population [latex]p[/latex] is given by [latex]G=f\left(p\right)[/latex]. [latex]G[/latex] is measured in tons per week, and [latex]p[/latex] is measured in thousands of people.
a. The town of Tola has a population of 40,000 and produces 13 tons of garbage each week. Express this information in terms of the function [latex]f[/latex].
b. Explain the meaning of the statement [latex]f\left(5\right)=2[/latex].
77. The number of cubic yards of dirt, [latex]D[/latex], needed to cover a garden with area [latex]a[/latex] square feet is given by [latex]D=g\left(a\right)[/latex].
a. A garden with area 5000 ft2 requires 50 yd3 of dirt. Express this information in terms of the function [latex]g[/latex].
b. Explain the meaning of the statement [latex]g\left(100\right)=1[/latex].
78. Let [latex]f\left(t\right)[/latex] be the number of ducks in a lake [latex]t[/latex] years after 1990. Explain the meaning of each statement:
a. [latex]f\left(5\right)=30[/latex]
b. [latex]f\left(10\right)=40[/latex]
79. Let [latex]h\left(t\right)[/latex] be the height above ground, in feet, of a rocket [latex]t[/latex] seconds after launching. Explain the meaning of each statement:
a. [latex]h\left(1\right)=200[/latex]
b. [latex]h\left(2\right)=350[/latex]
80. Show that the function [latex]f\left(x\right)=3{\left(x - 5\right)}^{2}+7[/latex] is not one-to-one.
See the next page for the solutions to the odd-numbered problems.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.