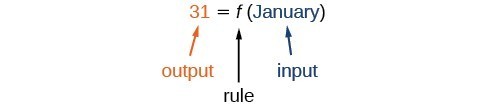
Learning Outcomes
- Define basic characteristics of functions.
- Recognize multiple representations of functions.
- Determine whether a relation represents a function.
- Properly use a function notation.
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
Basic definitions
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain of the relation and the set of the second components of each ordered pair is called the range of the relation. Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice the first.
[latex]\left\{\left(1,2\right),\left(2,4\right),\left(3,6\right),\left(4,8\right),\left(5,10\right)\right\}[/latex]
The domain is [latex]\left\{1,2,3,4,5\right\}[/latex]. The range is [latex]\left\{2,4,6,8,10\right\}[/latex].
Note the values in the domain are also known as an input values, or values of the independent variable, and are often labeled with the lowercase letter [latex]x[/latex]. Values in the range are also known as an output values, or values of the dependent variable, and are often labeled with the lowercase letter [latex]y[/latex].
A function [latex]f[/latex] is a relation that assigns a single value in the range to each value in the domain. In other words, no [latex]x[/latex]-values are used more than once. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, [latex]\left\{1,2,3,4,5\right\}[/latex], is paired with exactly one element in the range, [latex]\left\{2,4,6,8,10\right\}[/latex].
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
[latex]\left\{\left(\text{odd},1\right),\left(\text{even},2\right),\left(\text{odd},3\right),\left(\text{even},4\right),\left(\text{odd},5\right)\right\}[/latex]
Notice that each element in the domain, [latex]\left\{\text{even,}\text{odd}\right\}[/latex] is not paired with exactly one element in the range, [latex]\left\{1,2,3,4,5\right\}[/latex]. For example, the term “odd” corresponds to three values from the domain, [latex]\left\{1,3,5\right\}[/latex] and the term “even” corresponds to two values from the range, [latex]\left\{2,4\right\}[/latex]. This violates the definition of a function, so this relation is not a function.
This image compares relations that are functions and not functions.
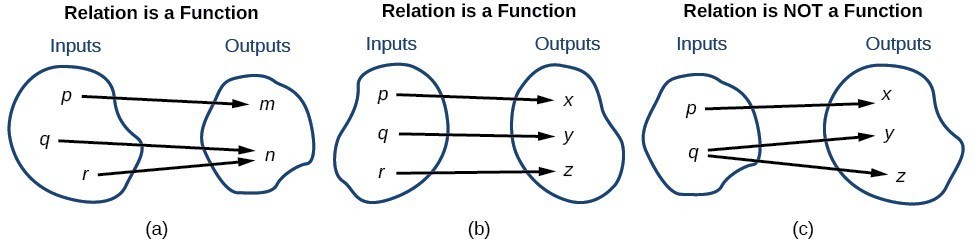
(a) This relationship is a function because each input is associated with a single output. Note that input [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. (b) This relationship is also a function. In this case, each input is associated with a single output. (c) This relationship is not a function because input [latex]q[/latex] is associated with two different outputs.
A General Note: FunctionS
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain, and the output values make up the range.
Representing Functions Using Tables
A common method of representing functions is in the form of a table. The table rows or columns display the corresponding input and output values. In some cases these values represent all we know about the relationship; other times the table provides a few select examples from a more complete relationship.
The table below lists the input number of each month (January = 1, February = 2, and so on) and the output value of the number of days in that month. This information represents all we know about the months and days for a given year (that is not a leap year). Note that, in this table, we define a days-in-a-month function [latex]f[/latex], where [latex]D=f\left(m\right)[/latex] identifies months by an integer rather than by name.
| Month number, [latex]m[/latex] (input) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Days in month, [latex]D[/latex] (output) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
The table below defines a function [latex]Q=g\left(n\right)[/latex]. Remember, this notation tells us that [latex]g[/latex] is the name of the function that takes the input [latex]n[/latex] and gives the output [latex]Q[/latex].
| [latex]n[/latex] | 1 | 2 | 3 | 4 | 5 |
| [latex]Q[/latex] | 8 | 6 | 7 | 6 | 8 |
The table below displays the age of children in years and their corresponding heights. This table displays just some of the data available for the heights and ages of children. We can see right away that this table does not represent a function because the same input value, 5 years, has two different output values, 40 in. and 42 in.
| Age in years, [latex]\text{ }a\text{ }[/latex] (input) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Height in inches, [latex]\text{ }h\text{ }[/latex] (output) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
How To: Given a table of input and output values, determine whether the table represents a function.
- Identify the input and output values.
- Check to see if each input value is paired with only one output value. If so, the table represents a function.
Example: Identifying Tables that Represent Functions
Which table, A, B, or C, represents a function (if any)?
| Table A | |
|---|---|
| Input | Output |
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Table B | |
|---|---|
| Input | Output |
| –3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Table C | |
|---|---|
| Input | Output |
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Example: Determining If Menu Price Lists Are Functions
The coffee shop menu consists of items and their prices.
- Is price a function of the item?
- Is the item a function of the price?

Example: Determining If Class Grade Rules Are Functions
In a particular math class, the overall percent grade corresponds to a grade point average. Is grade point average a function of the percent grade? Is the percent grade a function of the grade point average? The table below shows a possible rule for assigning grade points.
| Percent Grade | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
|---|---|---|---|---|---|---|---|---|
| Grade Point Average | 0.0 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Try It
The table below lists the five greatest baseball players of all time in order of rank.
| Player | Rank |
|---|---|
| Babe Ruth | 1 |
| Willie Mays | 2 |
| Ty Cobb | 3 |
| Walter Johnson | 4 |
| Hank Aaron | 5 |
- Is the rank a function of the player name?
- Is the player name a function of the rank?
Representing Functions Using Graphs
Another way we can represent a function is a graph. Graphs display a great many input-output pairs in a small space. The visual information they provide often makes relationships easier to understand. By convention, graphs are typically constructed with the input values along the horizontal axis and the output values along the vertical axis.
The most common graphs name the input value [latex]x[/latex] and the output value [latex]y[/latex], and we say [latex]y[/latex] is a function of [latex]x[/latex], or [latex]y=f\left(x\right)[/latex] when the function is named [latex]f[/latex]. The graph of the function is the set of all points [latex]\left(x,y\right)[/latex] in the plane that satisfies the equation [latex]y=f\left(x\right)[/latex]. If the function is defined for only a few input values, then the graph of the function is only a few points, where the x-coordinate of each point is an input value and the y-coordinate of each point is the corresponding output value. For example, the black dots on the graph in Figure 1 tell us that [latex]f\left(0\right)=2[/latex] and [latex]f\left(6\right)=1[/latex]. However, the set of all points [latex]\left(x,y\right)[/latex] satisfying [latex]y=f\left(x\right)[/latex] is a curve. The curve shown includes [latex]\left(0,2\right)[/latex] and [latex]\left(6,1\right)[/latex] because the curve passes through those points.

Figure 1
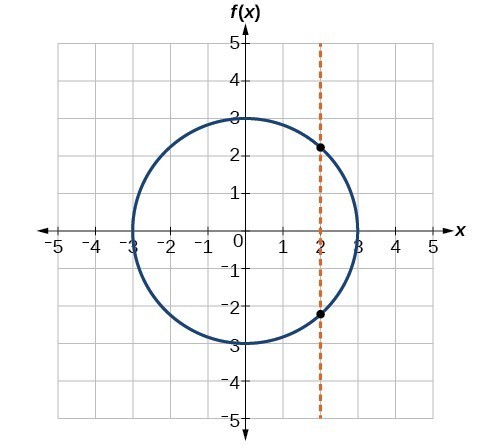
The vertical line test can be used to determine whether a graph represents a function. If we can draw any vertical line that intersects a graph more than once, then the graph does not define a function because a function has only one output value for each input value.

Figure 2
How To: Given a graph, use the vertical line test to determine if the graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, determine that the graph does not represent a function.
Example: Applying the Vertical Line Test
Which of the graphs represent(s) a function [latex]y=f\left(x\right)?[/latex]
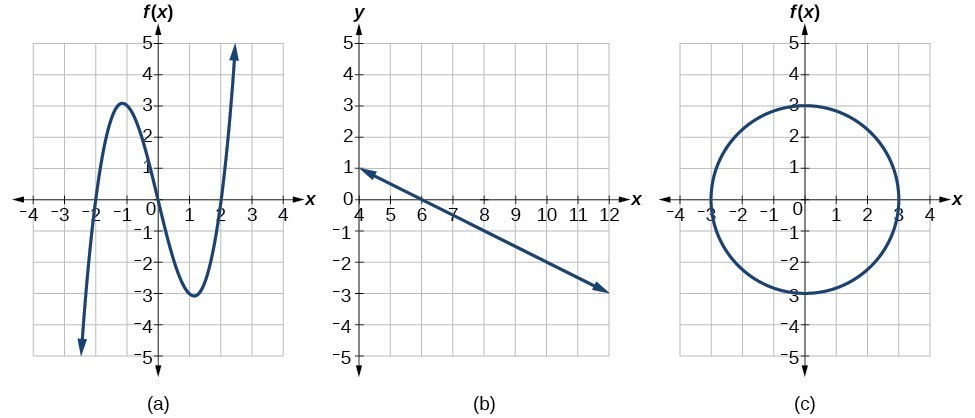
Figure 3
Try It
Does the graph in Figure 15 represent a function?

Figure 15
The following video summarizes the basic characteristics of functions as well as their different representations mentioned so far.
Using Function Notation
Once we determine that a relationship is a function, we need to display and define the functional relationships so that we can understand and use them, and sometimes also so that we can program them into computers. There are various ways of representing functions. A standard function notation is one representation that makes it easier to work with functions.
To represent “height is a function of age,” we start by identifying the descriptive variables [latex]h[/latex] for height and [latex]a[/latex] for age. The letters [latex]f,g[/latex], and [latex]h[/latex] are often used to represent functions just as we use [latex]x,y[/latex], and [latex]z[/latex] to represent numbers and [latex]A,B[/latex], and [latex]C[/latex] to represent sets.
[latex]\begin{align}&h\text{ is }f\text{ of }a &&\text{We name the function }f;\text{ height is a function of age}. \\ &h=f\left(a\right) &&\text{We use parentheses to indicate the function input}\text{. } \\ &f\left(a\right) &&\text{We name the function }f;\text{ the expression is read as }''f\text{ of }a''. \end{align}[/latex]
Remember, we can use any letter to name the function; we can use the notation [latex]h\left(a\right)[/latex] to show that [latex]h[/latex] depends on [latex]a[/latex]. The input value [latex]a[/latex] must be put into the function [latex]h[/latex] to get an output value. The parentheses indicate that age is input into the function; they do not indicate multiplication.
We can also give an algebraic expression as the input to a function. For example [latex]f\left(a+b\right)[/latex] means “first add [latex]a[/latex] and [latex]b[/latex], and the result is the input for the function [latex]f[/latex].” We must perform the operations in this order to obtain the correct result.
A General Note: Function Notation
The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. This is read as [latex]``y[/latex] is a function of [latex]x.''[/latex] The letter [latex]x[/latex] represents the input value, or independent variable. The letter [latex]y[/latex], or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable.
Example: Using Function Notation for Days in a Month
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month in a non-leap year.
Example: Interpreting Function Notation
A function [latex]N=f\left(y\right)[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f\left(2005\right)=300[/latex] represent?
Q & A
Instead of a notation such as [latex]y=f\left(x\right)[/latex], could we use the same symbol for the output as for the function, such as [latex]y=y\left(x\right)[/latex], meaning “y is a function of x?”
Yes, this is often done, especially in applied subjects that use higher math, such as physics and engineering. However, in exploring math itself we like to maintain a distinction between a function such as [latex]f[/latex], which is a rule or procedure, and the output [latex]y[/latex] we get by applying [latex]f[/latex] to a particular input [latex]x[/latex]. This is why we usually use notation such as [latex]y=f\left(x\right),P=W\left(d\right)[/latex], and so on.
Example: Applying the Vertical Line Test
Which of the graphs represent(s) a function [latex]y=f\left(x\right)?[/latex]
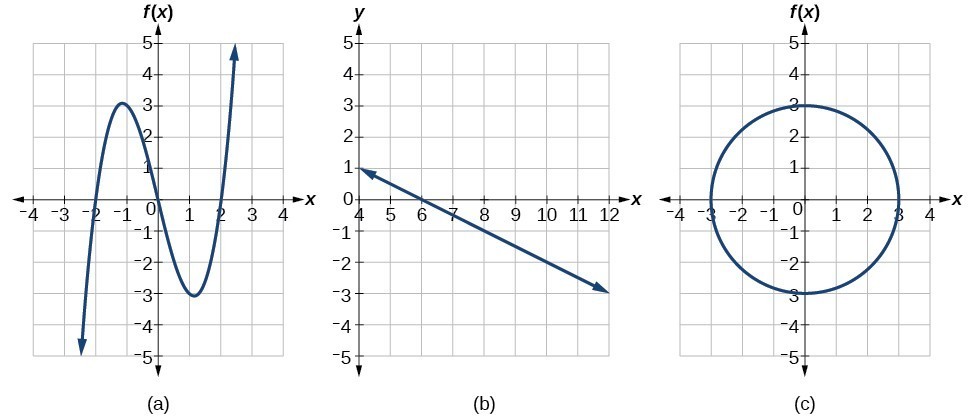
Try It
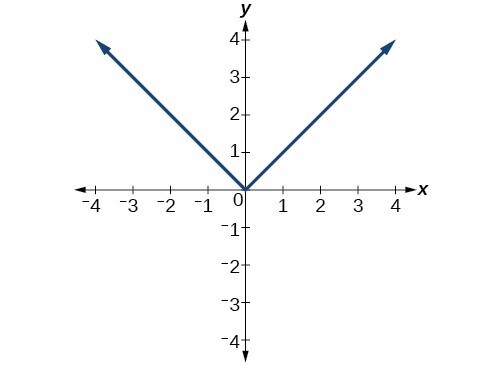
Does the graph below represent a function?
Key Concepts
- A relation is a set of ordered pairs. A function is a specific type of relation in which each domain value, or input, leads to exactly one range value, or output.
- Function notation is a shorthand method for relating the input to the output in the form [latex]y=f\left(x\right)[/latex].
- In table form, a function can be represented by rows or columns that relate to input and output values.
- An algebraic form of a function can be written from an equation.
- A graph represents a function if any vertical line drawn on the graph intersects the graph at no more than one point.
Glossary
- dependent variable
- an output variable
- domain
- the set of all possible input values for a relation
- function
- a relation in which each input value yields a unique output value
- independent variable
- an input variable
- input
- each object or value in a domain that relates to another object or value by a relationship known as a function
- output
- each object or value in the range that is produced when an input value is entered into a function
- range
- the set of output values that result from the input values in a relation
- relation
- a set of ordered pairs
- vertical line test
- a method of testing whether a graph represents a function by determining whether a vertical line intersects the graph no more than once
 Each item on the menu has only one price, so the price is a function of the item.
Each item on the menu has only one price, so the price is a function of the item. Therefore, the item is a not a function of price.
Therefore, the item is a not a function of price.