Problem Set: Unit Circle

1. Describe the unit circle.

2. What do the x- and y-coordinates of the points on the unit circle represent?

3. Discuss the difference between a coterminal angle and a reference angle.

4. Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.

5. Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.

For the following exercises, use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by [latex]t[/latex] lies.

6. [latex]\text{sin}\left(t\right)<0[/latex] and [latex]\text{cos}\left(t\right)<0[/latex]

7. [latex]\text{sin}\left(t\right)>0[/latex] and [latex]\cos \left(t\right)>0[/latex]

8. [latex]\sin \left(t\right)>0[/latex] and [latex]\cos \left(t\right)<0[/latex]

9. [latex]\sin \left(t\right)<0[/latex] and [latex]\cos \left(t\right)>0[/latex]

For the following exercises, find the exact value of each trigonometric function.

10. [latex]\sin \frac{\pi }{2}[/latex]

11. [latex]\sin \frac{\pi }{3}[/latex]

12. [latex]\cos \frac{\pi }{2}[/latex]

13. [latex]\cos \frac{\pi }{3}[/latex]

14. [latex]\sin \frac{\pi }{4}[/latex]

15. [latex]\cos \frac{\pi }{4}[/latex]

16. [latex]\sin \frac{\pi }{6}[/latex]

17. [latex]\sin \pi [/latex]

18. [latex]\sin \frac{3\pi }{2}[/latex]

19. [latex]\cos \pi [/latex]

20. [latex]\cos 0[/latex]

21. [latex]\cos \frac{\pi }{6}[/latex]

22. [latex]\sin 0[/latex]

For the following exercises, state the reference angle for the given angle.

23. [latex]240^\circ [/latex]

24. [latex]-170^\circ [/latex]

25. [latex]100^\circ [/latex]

26. [latex]-315^\circ [/latex]

27. [latex]135^\circ [/latex]

28. [latex]\frac{5\pi }{4}[/latex]

29. [latex]\frac{2\pi }{3}[/latex]

30. [latex]\frac{5\pi }{6}[/latex]

31. [latex]\frac{-11\pi }{3}[/latex]

32. [latex]\frac{-7\pi }{4}[/latex]

33. [latex]\frac{-\pi }{8}[/latex]

For the following exercises, find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle. If the angle is not one of the angles on the unit circle, use a calculator and round to three decimal places.

34. [latex]225^\circ [/latex]

35. [latex]300^\circ [/latex]

36. [latex]320^\circ [/latex]

37. [latex]135^\circ [/latex]

38. [latex]210^\circ [/latex]

39. [latex]120^\circ [/latex]

40. [latex]250^\circ [/latex]

41. [latex]150^\circ [/latex]

42. [latex]\frac{5\pi }{4}[/latex]

43. [latex]\frac{7\pi }{6}[/latex]

44. [latex]\frac{5\pi }{3}[/latex]

45. [latex]\frac{3\pi }{4}[/latex]

46. [latex]\frac{4\pi }{3}[/latex]

47. [latex]\frac{2\pi }{3}[/latex]

48. [latex]\frac{5\pi }{6}[/latex]

49. [latex]\frac{7\pi }{4}[/latex]

For the following exercises, find the requested value.

50. If [latex]\text{cos}\left(t\right)=\frac{1}{7}[/latex] and [latex]t[/latex] is in the 4th quadrant, find [latex]\text{sin}\left(t\right)[/latex].

51. If [latex]\text{cos}\left(t\right)=\frac{2}{9}[/latex] and [latex]t[/latex] is in the 1st quadrant, find [latex]\text{sin}\left(t\right)[/latex].

52. If [latex]\text{sin}\left(t\right)=\frac{3}{8}[/latex] and [latex]t[/latex] is in the 2nd quadrant, find [latex]\text{cos}\left(t\right)[/latex].

53. If [latex]\text{sin}\left(t\right)=-\frac{1}{4}[/latex] and [latex]t[/latex] is in the 3rd quadrant, find [latex]\text{cos}\left(t\right)[/latex].

54. Find the coordinates of the point on a circle with radius 15 corresponding to an angle of [latex]220^\circ [/latex].

55. Find the coordinates of the point on a circle with radius 20 corresponding to an angle of [latex]120^\circ [/latex].

56. Find the coordinates of the point on a circle with radius 8 corresponding to an angle of [latex]\frac{7\pi }{4}[/latex].

57. Find the coordinates of the point on a circle with radius 16 corresponding to an angle of [latex]\frac{5\pi }{9}[/latex].

58. State the domain of the sine and cosine functions.

59. State the range of the sine and cosine functions.

For the following exercises, use the given point on the unit circle to find the value of the sine and cosine of [latex]t[/latex].

60.
Graph of a quarter circle with angles of 0, 30, 45, 60, and 90 degrees inscribed. Equivalence of angles in radians shown. Points along circle are marked.

61.
Graph of circle with angle of t inscribed. Point of (negative square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.

62.
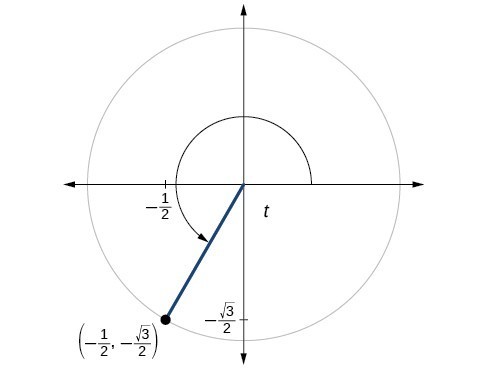
Graph of circle with angle of t inscribed. Point of (1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.

63.
Graph of circle with angle of t inscribed. Point of (negative square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.

64.
Graph of circle with angle of t inscribed. Point of (1/2, square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.

65.
Graph of circle with angle of t inscribed. Point of (-1/2, square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.

66.
Graph of circle with angle of t inscribed. Point of (-1/2, negative square root of 3 over 2) is at intersection of terminal side of angle and edge of circle.

67.
Graph of circle with angle of t inscribed. Point of (square root of 2 over 2, negative square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.

68.
Graph of circle with angle of t inscribed. Point of (1,0) is at intersection of terminal side of angle and edge of circle.

69.
Graph of circle with angle of t inscribed. Point of (-1,0) is at intersection of terminal side of angle and edge of circle.

70.
Graph of circle with angle of t inscribed. Point of (0.111,0.994) is at intersection of terminal side of angle and edge of circle.

71.
Graph of circle with angle of t inscribed. Point of (0.803,-0.596 is at intersection of terminal side of angle and edge of circle.

72.
Graph of circle with angle of t inscribed. Point of (negative square root of 2 over 2, square root of 2 over 2) is at intersection of terminal side of angle and edge of circle.

73.
Graph of circle with angle of t inscribed. Point of (square root of 3 over 2, 1/2) is at intersection of terminal side of angle and edge of circle.

74.
Graph of circle with angle of t inscribed. Point of (negative square root of 3 over 2, -1/2) is at intersection of terminal side of angle and edge of circle.

75.
Graph of circle with angle of t inscribed. Point of (square root of 3 over 2, -1/2) is at intersection of terminal side of angle and edge of circle.

76.
Graph of circle with angle of t inscribed. Point of (0, -1) is at intersection of terminal side of angle and edge of circle.

77.
Graph of circle with angle of t inscribed. Point of (-0.649, 0.761) is at intersection of terminal side of angle and edge of circle.

78.
Graph of circle with angle of t inscribed. Point of (-0.948, -0.317) is at intersection of terminal side of angle and edge of circle.

79.
Graph of circle with angle of t inscribed. Point of (0, 1) is at intersection of terminal side of angle and edge of circle.
For the following exercises, use a graphing calculator to evaluate.

80. [latex]\sin \frac{5\pi }{9}[/latex]

81. [latex]\cos \frac{5\pi }{9}[/latex]

82. [latex]\sin \frac{\pi }{10}[/latex]

83. [latex]\cos \frac{\pi }{10}[/latex]

84. [latex]\sin \frac{3\pi }{4}[/latex]

85. [latex]\cos \frac{3\pi }{4}[/latex]

86. [latex]\sin 98^\circ [/latex]

87. [latex]\cos 98^\circ [/latex]

88. [latex]\cos 310^\circ [/latex]

89. [latex]\sin 310^\circ [/latex]

90. [latex]\sin \left(\frac{11\pi }{3}\right)\cos \left(\frac{-5\pi }{6}\right)[/latex]

91. [latex]\sin \left(\frac{3\pi }{4}\right)\cos \left(\frac{5\pi }{3}\right)[/latex]

92. [latex]\sin \left(-\frac{4\pi }{3}\right)\cos \left(\frac{\pi }{2}\right)[/latex]

93. [latex]\sin \left(\frac{-9\pi }{4}\right)\cos \left(\frac{-\pi }{6}\right)[/latex]

94. [latex]\sin \left(\frac{\pi }{6}\right)\cos \left(\frac{-\pi }{3}\right)[/latex]

95. [latex]\sin \left(\frac{7\pi }{4}\right)\cos \left(\frac{-2\pi }{3}\right)[/latex]

96. [latex]\cos \left(\frac{5\pi }{6}\right)\cos \left(\frac{2\pi }{3}\right)[/latex]

97. [latex]\cos \left(\frac{-\pi }{3}\right)\cos \left(\frac{\pi }{4}\right)[/latex]

98. [latex]\sin \left(\frac{-5\pi }{4}\right)\sin \left(\frac{11\pi }{6}\right)[/latex]

99. [latex]\sin \left(\pi \right)\sin \left(\frac{\pi }{6}\right)[/latex]

For the following exercises, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point [latex]\left(0,1\right)[/latex], that is, on the due north position. Assume the carousel revolves counter clockwise.

100. What are the coordinates of the child after 45 seconds?

101. What are the coordinates of the child after 90 seconds?

102. What is the coordinates of the child after 125 seconds?

103. When will the child have coordinates [latex]\left(0.707,-0.707\right)[/latex] if the ride lasts 6 minutes? (There are multiple answers.)

104. When will the child have coordinates [latex]\left(-0.866,-0.5\right)[/latex] if the ride last 6 minutes?