We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the y-coordinate on the unit circle, the other angle with the same sine will share the same y-value, but have the opposite x-value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.
Likewise, there will be an angle in the fourth quadrant with the same cosine as the original angle. The angle with the same cosine will share the same x-value but will have the opposite y-value. Therefore, its sine value will be the opposite of the original angle’s sine value.
As shown in Figure 16, angle [latex]\alpha [/latex] has the same sine value as angle [latex]t[/latex]; the cosine values are opposites. Angle [latex]\beta [/latex] has the same cosine value as angle [latex]t[/latex]; the sine values are opposites.
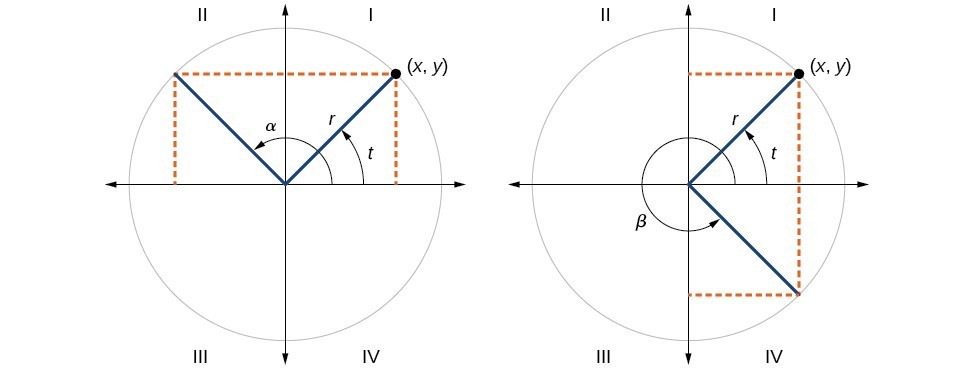
Figure 16
Recall that an angle’s reference angle is the acute angle, [latex]t[/latex], formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. A reference angle is always an angle between [latex]0[/latex] and [latex]90^\circ [/latex], or [latex]0[/latex] and [latex]\frac{\pi }{2}[/latex] radians. As we can see from Figure 17, for any angle in quadrants II, III, or IV, there is a reference angle in quadrant I.
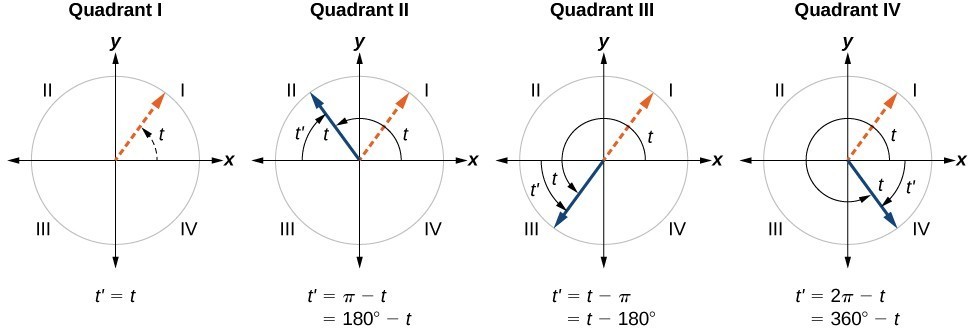
Figure 17
How To: Given an angle between [latex]0[/latex] and [latex]2\pi [/latex], find its reference angle.
- An angle in the first quadrant is its own reference angle.
- For an angle in the second or third quadrant, the reference angle is [latex]|\pi -t|[/latex] or [latex]|180^\circ \mathrm{-t}|[/latex].
- For an angle in the fourth quadrant, the reference angle is [latex]2\pi -t[/latex] or [latex]360^\circ \mathrm{-t}[/latex].
- If an angle is less than [latex]0[/latex] or greater than [latex]2\pi [/latex], add or subtract [latex]2\pi [/latex] as many times as needed to find an equivalent angle between [latex]0[/latex] and [latex]2\pi [/latex].
Example 5: Finding a Reference Angle
Find the reference angle of [latex]225^\circ [/latex] as shown in Figure 18.
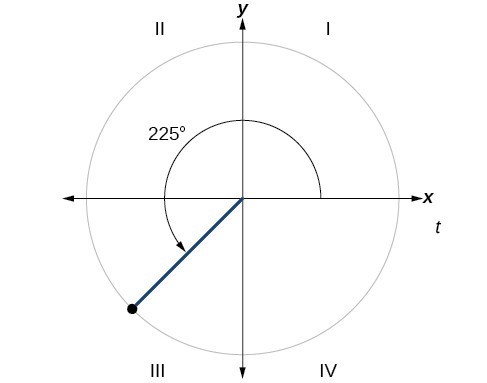
Figure 18
Solution
Because [latex]225^\circ [/latex] is in the third quadrant, the reference angle is
Using Reference Angles
Now let’s take a moment to reconsider the Ferris wheel introduced at the beginning of this section. Suppose a rider snaps a photograph while stopped twenty feet above ground level. The rider then rotates three-quarters of the way around the circle. What is the rider’s new elevation? To answer questions such as this one, we need to evaluate the sine or cosine functions at angles that are greater than 90 degrees or at a negative angle. Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. They can also be used to find [latex]\left(x,y\right)[/latex] coordinates for those angles. We will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies.
Using Reference Angles to Evaluate Trigonometric Functions
We can find the cosine and sine of any angle in any quadrant if we know the cosine or sine of its reference angle. The absolute values of the cosine and sine of an angle are the same as those of the reference angle. The sign depends on the quadrant of the original angle. The cosine will be positive or negative depending on the sign of the x-values in that quadrant. The sine will be positive or negative depending on the sign of the y-values in that quadrant.
A General Note: Using Reference Angles to Find Cosine and Sine
Angles have cosines and sines with the same absolute value as their reference angles. The sign (positive or negative) can be determined from the quadrant of the angle.
How To: Given an angle in standard position, find the reference angle, and the cosine and sine of the original angle.
- Measure the angle between the terminal side of the given angle and the horizontal axis. That is the reference angle.
- Determine the values of the cosine and sine of the reference angle.
- Give the cosine the same sign as the x-values in the quadrant of the original angle.
- Give the sine the same sign as the y-values in the quadrant of the original angle.
Example 5: Using Reference Angles to Find Sine and Cosine
- Using a reference angle, find the exact value of [latex]\cos \left(150^\circ \right)[/latex] and [latex]\text{sin}\left(150^\circ \right)[/latex].
- Using the reference angle, find [latex]\cos \frac{5\pi }{4}[/latex] and [latex]\sin \frac{5\pi }{4}[/latex].
Solution
- 150° is located in the second quadrant. The angle it makes with the x-axis is 180° − 150° = 30°, so the reference angle is 30°.This tells us that 150° has the same sine and cosine values as 30°, except for the sign. We know that
[latex]\cos \left(30^\circ \right)=\frac{\sqrt{3}}{2}\text{and}\sin \left(30^\circ \right)=\frac{1}{2}[/latex].
Since 150° is in the second quadrant, the x-coordinate of the point on the circle is negative, so the cosine value is negative. The y-coordinate is positive, so the sine value is positive.
[latex]\cos \left(150^\circ \right)=-\frac{\sqrt{3}}{2}\text{and}\sin \left(150^\circ \right)=\frac{1}{2}[/latex] - [latex]\frac{5\pi }{4}[/latex] is in the third quadrant. Its reference angle is [latex]\frac{5\pi }{4}-\pi =\frac{\pi }{4}[/latex]. The cosine and sine of [latex]\frac{\pi }{4}[/latex] are both [latex]\frac{\sqrt{2}}{2}[/latex]. In the third quadrant, both [latex]x[/latex] and [latex]y[/latex] are negative, so:
[latex]\cos \frac{5\pi }{4}=-\frac{\sqrt{2}}{2}\text{and}\sin \frac{5\pi }{4}=-\frac{\sqrt{2}}{2}[/latex]
Try It 6
a. Use the reference angle of [latex]315^\circ [/latex] to find [latex]\cos \left(315^\circ \right)[/latex] and [latex]\sin \left(315^\circ \right)[/latex].
b. Use the reference angle of [latex]-\frac{\pi }{6}[/latex] to find [latex]\cos \left(-\frac{\pi }{6}\right)[/latex] and [latex]\sin \left(-\frac{\pi }{6}\right)[/latex].
Using Reference Angles to Find Coordinates
Now that we have learned how to find the cosine and sine values for special angles in the first quadrant, we can use symmetry and reference angles to fill in cosine and sine values for the rest of the special angles on the unit circle. They are shown in Figure 19. Take time to learn the [latex]\left(x,y\right)[/latex] coordinates of all of the major angles in the first quadrant.
In addition to learning the values for special angles, we can use reference angles to find [latex]\left(x,y\right)[/latex] coordinates of any point on the unit circle, using what we know of reference angles along with the identities
First we find the reference angle corresponding to the given angle. Then we take the sine and cosine values of the reference angle, and give them the signs corresponding to the y– and x-values of the quadrant.
How To: Given the angle of a point on a circle and the radius of the circle, find the [latex]\left(x,y\right)[/latex] coordinates of the point.
- Find the reference angle by measuring the smallest angle to the x-axis.
- Find the cosine and sine of the reference angle.
- Determine the appropriate signs for [latex]x[/latex] and [latex]y[/latex]
in the given quadrant.
Example 6: Using the Unit Circle to Find Coordinates
Find the coordinates of the point on the unit circle at an angle of [latex]\frac{7\pi }{6}[/latex].
Solution
We know that the angle [latex]\frac{7\pi }{6}[/latex] is in the third quadrant.
First, let’s find the reference angle by measuring the angle to the x-axis. To find the reference angle of an angle whose terminal side is in quadrant III, we find the difference of the angle and [latex]\pi [/latex].
Next, we will find the cosine and sine of the reference angle:
We must determine the appropriate signs for x and y in the given quadrant. Because our original angle is in the third quadrant, where both [latex]x[/latex] and [latex]y[/latex] are negative, both cosine and sine are negative.
Now we can calculate the [latex]\left(x,y\right)[/latex] coordinates using the identities [latex]x=\cos \theta [/latex] and [latex]y=\sin \theta [/latex].
The coordinates of the point are [latex]\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right)[/latex] on the unit circle.
Try It 7
Find the coordinates of the point on the unit circle at an angle of [latex]\frac{5\pi }{3}[/latex].
