Solutions to Odd-Numbered Exercises

1. Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.

3. exponential; the population decreases by a proportional rate.

5. not exponential; the charge decreases by a constant amount each visit, so the statement represents a linear function.

7. The forest represented by the function [latex]B\left(t\right)=82{\left(1.029\right)}^{t}[/latex].

9. After t = 20 years, forest A will have 43 more trees than forest B.

11. Answers will vary. Sample response: For a number of years, the population of forest A will increasingly exceed forest B, but because forest B actually grows at a faster rate, the population will eventually become larger than forest A and will remain that way as long as the population growth models hold. Some factors that might influence the long-term validity of the exponential growth model are drought, an epidemic that culls the population, and other environmental and biological factors.

13. exponential growth; The growth factor, 1.06, is greater than 1.

15. exponential decay; The decay factor, 0.97, is between 0 and 1.

17. [latex]f\left(x\right)=2000{\left(0.1\right)}^{x}[/latex]

19. continuous growth; the growth rate is greater than 0.

21. continuous decay; the growth rate is less than 0.

23. [latex]f\left(-1\right)=-4[/latex]

25. [latex]f\left(-1\right)\approx -0.2707[/latex]

27. [latex]f\left(3\right)\approx 483.8146[/latex]

29. 47,622 fox

31. 1.39%; $155,368.09

33.

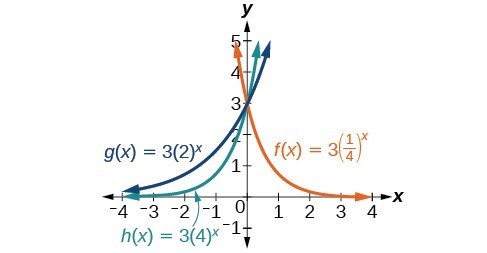
35. B

37. A

39. E

41. D

43. C

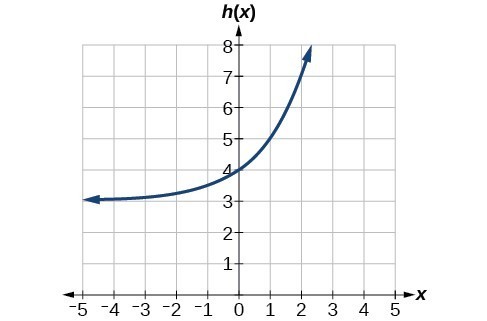
45. Horizontal asymptote: [latex]h\left(x\right)=3[/latex]; Domain: all real numbers; Range: all real numbers strictly greater than 3.

47. [latex]g\left(6\right)=800+\frac{1}{3}\approx 800.3333[/latex]

49. [latex]h\left(-7\right)=-58[/latex]