Learning Objectives
In this section, you will:
- Solve applied problems using the Law of Sines.
The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.
Example: Finding an Altitude
Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in (Figure 16). Round the altitude to the nearest tenth of a mile.
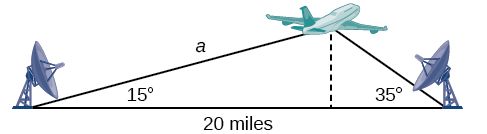
Figure 16.
Try it
The diagram shown in (Figure 17) represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is 70°, the angle of elevation from the northern end zone, point[latex],B,,[/latex]is 62°, and the distance between the viewing points of the two end zones is 145 yards.
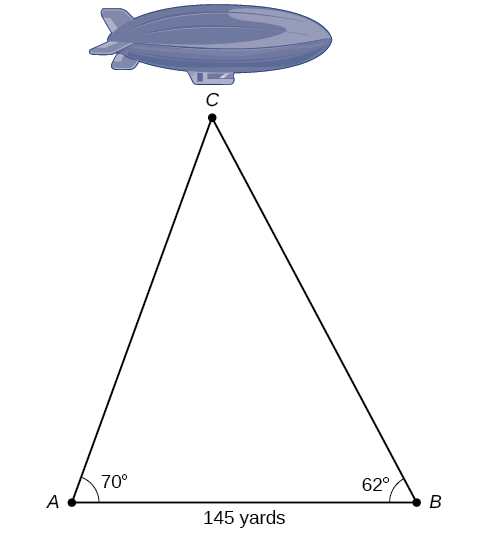
Figure 17.
Glossary
- altitude
- a perpendicular line from one vertex of a triangle to the opposite side, or in the case of an obtuse triangle, to the line containing the opposite side, forming two right triangles
- ambiguous case
- a scenario in which more than one triangle is a valid solution for a given oblique SSA triangle
- Law of Sines
- states that the ratio of the measurement of one angle of a triangle to the length of its opposite side is equal to the remaining two ratios of angle measure to opposite side; any pair of proportions may be used to solve for a missing angle or side
- oblique triangle
- any triangle that is not a right triangle