Using Trigonometric Functions
In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.
How To: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.
- For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
- Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
- Using the value of the trigonometric function and the known side length, solve for the missing side length.
Example 5: Finding Missing Side Lengths Using Trigonometric Ratios
Find the unknown sides of the triangle in Figure 11.
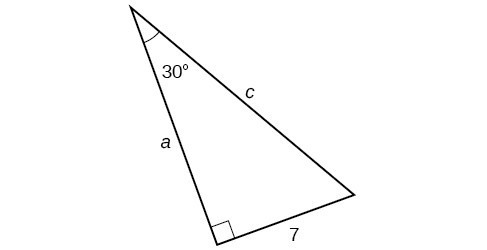
Figure 11
Solution
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.
We rearrange to solve for [latex]a[/latex].
We can use the sine to find the hypotenuse.
Again, we rearrange to solve for [latex]c[/latex].
Try It 5
A right triangle has one angle of [latex]\frac{\pi }{3}[/latex] and a hypotenuse of 20. Find the unknown sides and angle of the triangle.
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye.
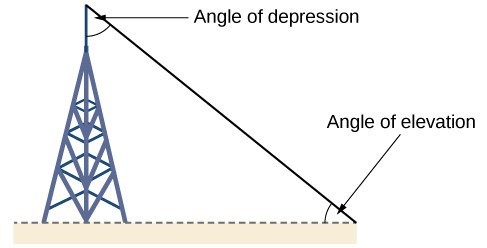
Figure 12
How To: Given a tall object, measure its height indirectly.
- Make a sketch of the problem situation to keep track of known and unknown information.
- Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
- At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
- Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
- Solve the equation for the unknown height.
Example 6: Measuring a Distance Indirectly
To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of [latex]57^\circ[/latex] between a line of sight to the top of the tree and the ground, as shown in Figure 13. Find the height of the tree.
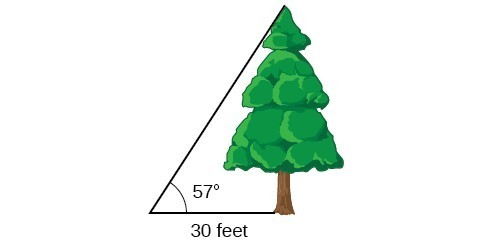
Figure 13
Solution
We know that the angle of elevation is [latex]57^\circ[/latex] and the adjacent side is 30 ft long. The opposite side is the unknown height.
The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of [latex]57^\circ[/latex], letting [latex]h[/latex] be the unknown height.
The tree is approximately 46 feet tall.
Try It 6
How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of [latex]\frac{5\pi }{12}[/latex] with the ground? Round to the nearest foot.
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution
- Example: Determine the Length of a Side of a Right Triangle Using a Trig Equation. Authored by: Mathispower4u. Located at: https://youtu.be/8jU2R3BuR5E. License: All Rights Reserved. License Terms: Standard YouTube License