Finding Magnitude and Direction

To work with a vector, we need to be able to find its magnitude and its direction. We find its magnitude using the Pythagorean Theorem or the distance formula, and we find its direction using the inverse tangent function.

A General Note: Magnitude and Direction of a Vector

Given a position vector [latex]v[/latex] [latex]=\langle a,b\rangle [/latex], the magnitude is found by [latex]|v|=\sqrt{{a}^{2}+{b}^{2}}[/latex]. The direction is equal to the angle formed with the x-axis, or with the y-axis, depending on the application. For a position vector, the direction is found by [latex]\tan \theta =\left(\frac{b}{a}\right)\Rightarrow \theta ={\tan }^{-1}\left(\frac{b}{a}\right)[/latex], as illustrated in Figure 5.

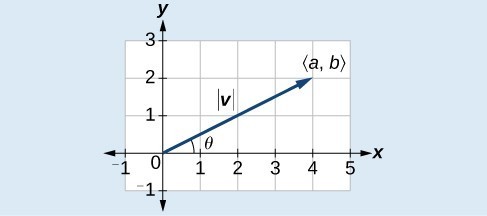
Standard plot of a position vector (a,b) with magnitude |v| extending into Q1 at theta degrees.

Figure 5

Two vectors v and u are considered equal if they have the same magnitude and the same direction. Additionally, if both vectors have the same position vector, they are equal.

Example 3: Finding the Magnitude and Direction of a Vector

Find the magnitude and direction of the vector with initial point [latex]P\left(-8,1\right)[/latex] and terminal point [latex]Q\left(-2,-5\right)[/latex]. Draw the vector.

Solution

First, find the position vector.

[latex]\begin{array}{l}u=\langle -2,-\left(-8\right),-5 - 1\rangle \hfill \\ \text{ }=\langle 6,-6\rangle \hfill \end{array}[/latex]

We use the Pythagorean Theorem to find the magnitude.

[latex]\begin{array}{l}|u|=\sqrt{{\left(6\right)}^{2}+{\left(-6\right)}^{2}}\hfill \\ =\sqrt{72}\hfill \\ =6\sqrt{2}\hfill \end{array}[/latex]

The direction is given as

[latex]\begin{array}{l}\tan \theta =\frac{-6}{6}=-1\Rightarrow \theta ={\tan }^{-1}\left(-1\right)\hfill \\ =-45^\circ \hfill \end{array}[/latex]

However, the angle terminates in the fourth quadrant, so we add 360° to obtain a positive angle. Thus, [latex]-45^\circ +360^\circ =315^\circ [/latex].

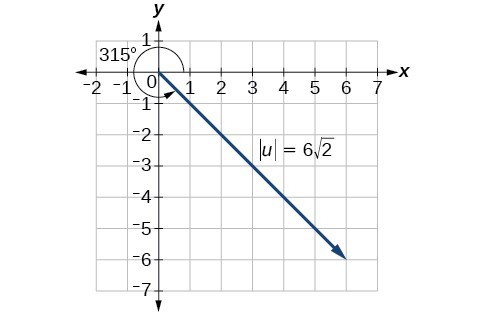
Plot of the position vector extending into Q4 from the origin with the magnitude 6rad2.

Figure 6

Example 4: Showing That Two Vectors Are Equal

Show that vector v with initial point at [latex]\left(5,-3\right)[/latex] and terminal point at [latex]\left(-1,2\right)[/latex] is equal to vector u with initial point at [latex]\left(-1,-3\right)[/latex] and terminal point at [latex]\left(-7,2\right)[/latex]. Draw the position vector on the same grid as v and u. Next, find the magnitude and direction of each vector.

Solution

As shown in Figure 7, draw the vector [latex]v[/latex] starting at initial [latex]\left(5,-3\right)[/latex] and terminal point [latex]\left(-1,2\right)[/latex]. Draw the vector [latex]u[/latex] with initial point [latex]\left(-1,-3\right)[/latex] and terminal point [latex]\left(-7,2\right)[/latex]. Find the standard position for each.

Next, find and sketch the position vector for v and u. We have

[latex]\begin{array}{l}v=\langle -1 - 5,2-\left(-3\right)\rangle \hfill \\ \text{ }=\langle -6,5\rangle \hfill \\ \hfill \\ u=\langle -7-\left(-1\right),2-\left(-3\right)\rangle \hfill \\ \text{ }=\langle -6,5\rangle \hfill \end{array}[/latex]

Since the position vectors are the same, v and u are the same.

An alternative way to check for vector equality is to show that the magnitude and direction are the same for both vectors. To show that the magnitudes are equal, use the Pythagorean Theorem.

[latex]\begin{array}{l}|v|=\sqrt{{\left(-1 - 5\right)}^{2}+{\left(2-\left(-3\right)\right)}^{2}}\hfill \\ =\sqrt{{\left(-6\right)}^{2}+{\left(5\right)}^{2}}\hfill \\ =\sqrt{36+25}\hfill \\ =\sqrt{61}\hfill \\ |u|=\sqrt{{\left(-7-\left(-1\right)\right)}^{2}+{\left(2-\left(-3\right)\right)}^{2}}\hfill \\ =\sqrt{{\left(-6\right)}^{2}+{\left(5\right)}^{2}}\hfill \\ =\sqrt{36+25}\hfill \\ =\sqrt{61}\hfill \end{array}[/latex]

As the magnitudes are equal, we now need to verify the direction. Using the tangent function with the position vector gives

[latex]\begin{array}{l}\tan \theta =-\frac{5}{6}\Rightarrow \theta ={\tan }^{-1}\left(-\frac{5}{6}\right)\hfill \\ =-39.8^\circ \hfill \end{array}[/latex]

However, we can see that the position vector terminates in the second quadrant, so we add [latex]180^\circ [/latex]. Thus, the direction is [latex]-39.8^\circ +180^\circ =140.2^\circ [/latex].

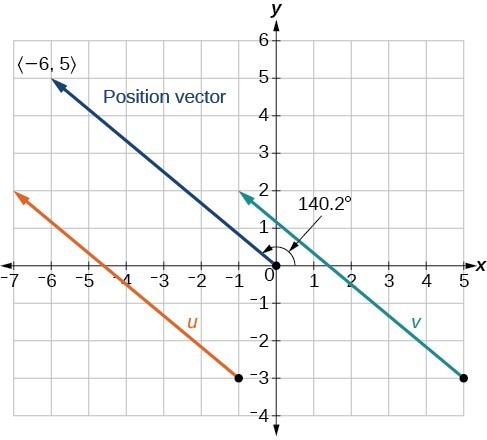
Plot of the two given vectors their same position vector.

Figure 7