Properly defining an angle first requires that we define a ray. A ray consists of one point on a line and all points extending in one direction from that point. The first point is called the endpoint of the ray. We can refer to a specific ray by stating its endpoint and any other point on it. The ray in Figure 1 can be named as ray EF, or in symbol form [latex]\stackrel{\to }{EF}[/latex].

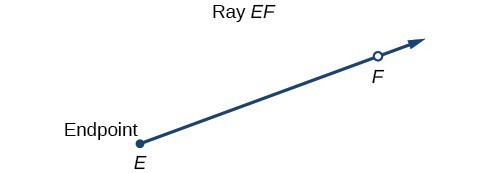
Figure 1

An angle is the union of two rays having a common endpoint. The endpoint is called the vertex of the angle, and the two rays are the sides of the angle. The angle in Figure 2 is formed from [latex]\stackrel{\to }{ED}[/latex] and [latex]\stackrel{\to }{EF}[/latex]. Angles can be named using a point on each ray and the vertex, such as angle DEF, or in symbol form [latex]\text{\hspace{0.17em}\angle }DEF[/latex].

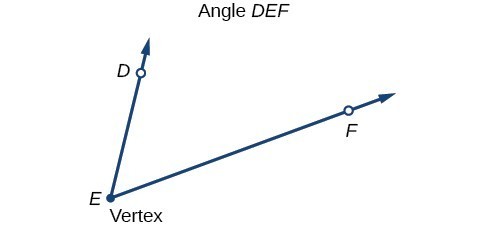
Figure 2

Greek letters are often used as variables for the measure of an angle. The table below is a list of Greek letters commonly used to represent angles, and a sample angle is shown in Figure 2.

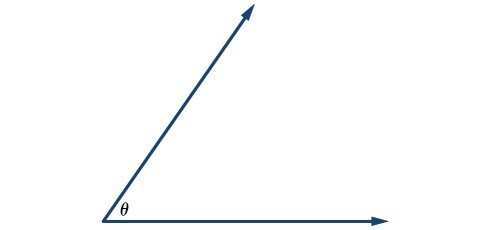
Figure 3. Angle theta, shown as [latex]\angle \theta[/latex]

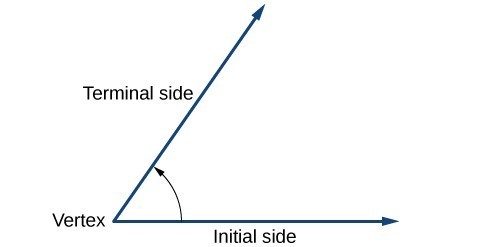
Figure 4

Angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side, and the rotated ray is the terminal side. In order to identify the different sides, we indicate the rotation with a small arc and arrow close to the vertex as in Figure 4.

The following video provides an illustration of angles in standard position.

As we discussed at the beginning of the section, there are many applications for angles, but in order to use them correctly, we must be able to measure them. The measure of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. One degree is [latex]\frac{1}{360}[/latex] of a circular rotation, so a complete circular rotation contains 360 degrees. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol °. For example, 90 degrees = 90°.

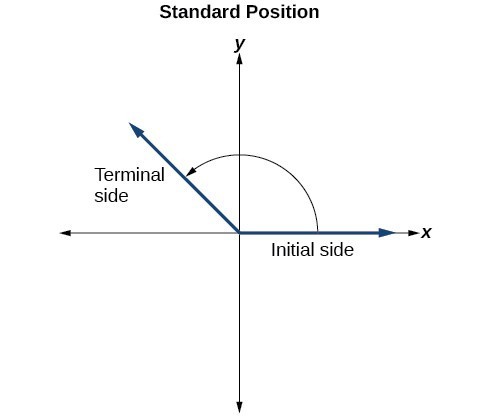
Figure 5

To formalize our work, we will begin by drawing angles on an x–y coordinate plane. Angles can occur in any position on the coordinate plane, but for the purpose of comparison, the convention is to illustrate them in the same position whenever possible. An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x-axis. 

If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle. If the angle is measured in a clockwise direction, the angle is said to be a negative angle.

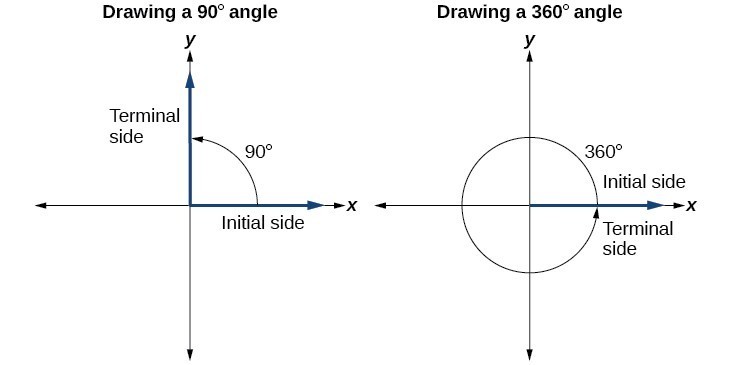
Figure 6

Drawing an angle in standard position always starts the same way—draw the initial side along the positive x-axis. To place the terminal side of the angle, we must calculate the fraction of a full rotation the angle represents. We do that by dividing the angle measure in degrees by 360°. For example, to draw a 90° angle, we calculate that [latex]\frac{90^\circ }{360^\circ }=\frac{1}{4}[/latex]. So, the terminal side will be one-fourth of the way around the circle, moving counterclockwise from the positive x-axis. To draw a 360° angle, we calculate that [latex]\frac{360^\circ }{360^\circ }=1[/latex]. So the terminal side will be 1 complete rotation around the circle, moving counterclockwise from the positive x-axis. In this case, the initial side and the terminal side overlap.

Since we define an angle in standard position by its terminal side, we have a special type of angle whose terminal side lies on an axis, a quadrantal angle. This type of angle can have a measure of 0°, 90°, 180°, 270° or 360°.

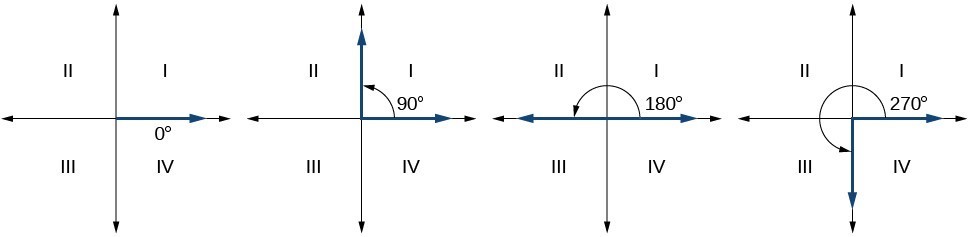
Figure 7. Quadrantal angles have a terminal side that lies along an axis. Examples are shown.