Converting between degrees and radians can make working with angles easier in some applications. For other applications, we may need another type of conversion. Negative angles and angles greater than a full revolution are more awkward to work with than those in the range of 0° to 360°, or 0 to [latex]2\pi [/latex]. It would be convenient to replace those out-of-range angles with a corresponding angle within the range of a single revolution.

It is possible for more than one angle to have the same terminal side. Look at Figure 16. The angle of 140° is a positive angle, measured counterclockwise. The angle of –220° is a negative angle, measured clockwise. But both angles have the same terminal side. If two angles in standard position have the same terminal side, they are coterminal angles. Every angle greater than 360° or less than 0° is coterminal with an angle between 0° and 360°, and it is often more convenient to find the coterminal angle within the range of 0° to 360° than to work with an angle that is outside that range.

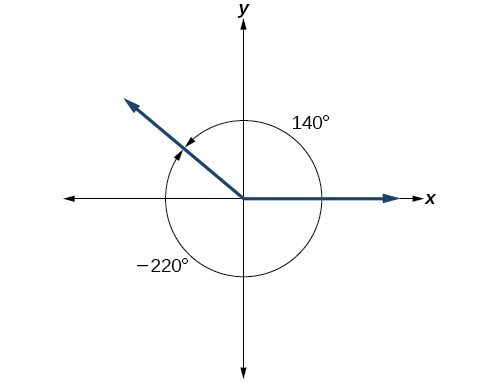
Figure 16. An angle of 140° and an angle of –220° are coterminal angles.

This video shows examples of how to determine if two angles are coterminal.

Any angle has infinitely many coterminal angles because each time we add 360° to that angle—or subtract 360° from it—the resulting value has a terminal side in the same location. For example, 100° and 460° are coterminal for this reason, as is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.

An angle’s reference angle is the measure of the smallest, positive, acute angle [latex]t[/latex] formed by the terminal side of the angle [latex]t[/latex] and the horizontal axis. Thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. See Figure 17 for examples of reference angles for angles in different quadrants.

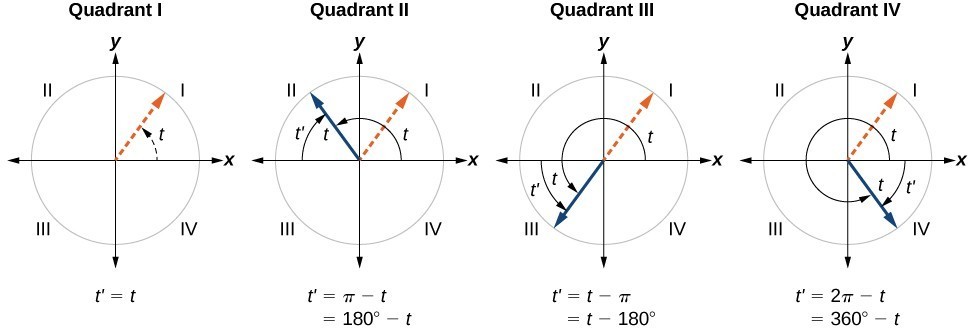
Figure 17

Solution

An angle with measure 800° is coterminal with an angle with measure 800 − 360 = 440°, but 440° is still greater than 360°, so we subtract 360° again to find another coterminal angle: 440 − 360 = 80°.

The angle [latex]\theta =80^\circ [/latex] is coterminal with 800°. To put it another way, 800° equals 80° plus two full rotations, as shown in Figure 18.

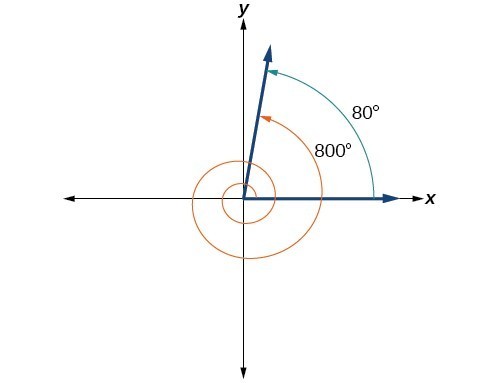
Figure 18

Solution

Since 45° is half of 90°, we can start at the positive horizontal axis and measure clockwise half of a 90° angle.

Because we can find coterminal angles by adding or subtracting a full rotation of 360°, we can find a positive coterminal angle here by adding 360°:

[latex]-45^\circ +360^\circ =315^\circ [/latex]

We can then show the angle on a circle, as in Figure 19.

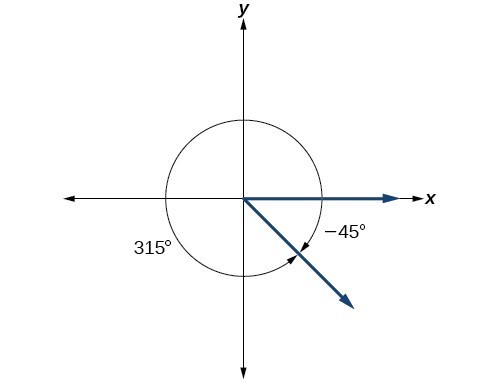
Figure 19

Finding Coterminal Angles Measured in Radians

We can find coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, we find coterminal angles by adding or subtracting one or more full rotations.

Solution

When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Likewise, in radians, we can find coterminal angles by adding or subtracting full rotations of [latex]2\pi [/latex] radians:

[latex]\begin{array}{l}\frac{19\pi }{4}-2\pi =\frac{19\pi }{4}-\frac{8\pi }{4}\hfill \\ =\frac{11\pi }{4}\hfill \end{array}[/latex]

The angle [latex]\frac{11\pi }{4}[/latex] is coterminal, but not less than [latex]2\pi [/latex], so we subtract another rotation:

[latex]\begin{array}{l}\frac{11\pi }{4}-2\pi =\frac{11\pi }{4}-\frac{8\pi }{4}\hfill \\ =\frac{3\pi }{4}\hfill \end{array}[/latex]

The angle [latex]\frac{3\pi }{4}[/latex] is coterminal with [latex]\frac{19\pi }{4}[/latex], as shown in Figure 20.

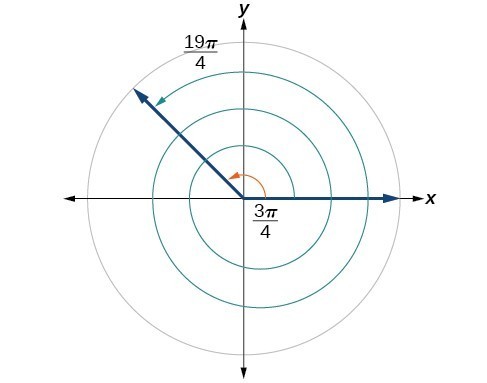
Figure 20