1. For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.

2. When a right triangle with a hypotenuse of 1 is placed in the unit circle, which sides of the triangle correspond to the x– and y-coordinates?

3. The tangent of an angle compares which sides of the right triangle?

4. What is the relationship between the two acute angles in a right triangle?

5. Explain the cofunction identity.

For the following exercises, use cofunctions of complementary angles.

6. [latex]\cos \left(\text{34^\circ }\right)=\sin \left(\text{__^\circ }\right)[/latex]

7. [latex]\cos \left(\frac{\pi }{3}\right)=\sin \text{(___)}[/latex]

8. [latex]\csc \left(\text{21^\circ }\right)=\sec \left(\text{___^\circ }\right)[/latex]

9. [latex]\tan \left(\frac{\pi }{4}\right)=\cot \left(\text{__}\right)[/latex]

For the following exercises, find the lengths of the missing sides if side [latex]a[/latex] is opposite angle [latex]A[/latex], side [latex]b[/latex] is opposite angle [latex]B[/latex], and side [latex]c[/latex] is the hypotenuse.

10. [latex]\cos B=\frac{4}{5},a=10[/latex]

11. [latex]\sin B=\frac{1}{2}, a=20[/latex]

12. [latex]\tan A=\frac{5}{12},b=6[/latex]

13. [latex]\tan A=100,b=100[/latex]

14. [latex]\sin B=\frac{1}{\sqrt{3}}, a=2[/latex]

15. [latex]a=5,\measuredangle A={60}^{\circ }[/latex]

16. [latex]c=12,\measuredangle A={45}^{\circ }[/latex]

For the following exercises, use Figure 14 to evaluate each trigonometric function of angle [latex]A[/latex].

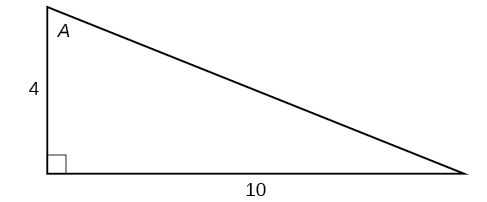
Figure 14

17. [latex]\sin A[/latex]

18. [latex]\cos A[/latex]

19. [latex]\tan A[/latex]

20. [latex]\csc A[/latex]

21. [latex]\sec A[/latex]

22. [latex]\cot A[/latex]

For the following exercises, use Figure 15 to evaluate each trigonometric function of angle [latex]A[/latex].

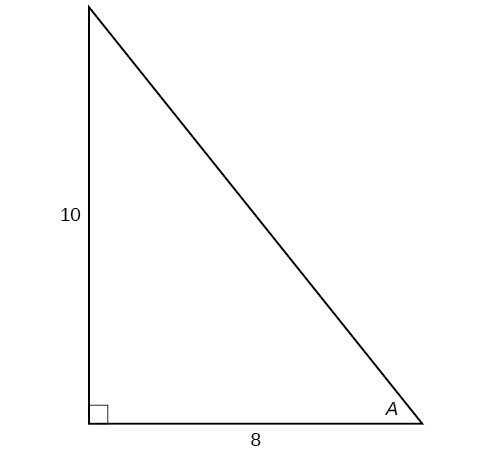
Figure 15

23. [latex]\sin A[/latex]

24. [latex]\cos A[/latex]

25. [latex]\tan A[/latex]

26. [latex]\csc A[/latex]

27. [latex]\sec A[/latex]

28. [latex]\cot A[/latex]

For the following exercises, solve for the unknown sides of the given triangle.

29.

30.

31.

For the following exercises, use a calculator to find the length of each side to four decimal places.

32.

33.

34.

35.

36.

37. [latex]b=15,\measuredangle B={15}^{\circ }[/latex]

38. [latex]c=200,\measuredangle B={5}^{\circ }[/latex]

39. [latex]c=50,\measuredangle B={21}^{\circ }[/latex]

40. [latex]a=30,\measuredangle A={27}^{\circ }[/latex]

41. [latex]b=3.5,\measuredangle A={78}^{\circ }[/latex]

42. Find [latex]x[/latex].

43. Find [latex]x[/latex].

44. Find [latex]x[/latex].

45. Find [latex]x[/latex].

46. A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]36^\circ[/latex], and that the angle of depression to the bottom of the tower is [latex]23^\circ[/latex]. How tall is the tower?

47. A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]43^\circ[/latex], and that the angle of depression to the bottom of the tower is [latex]31^\circ[/latex]. How tall is the tower?

48. A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]15^\circ[/latex], and that the angle of depression to the bottom of the tower is [latex]2^\circ[/latex]. How far is the person from the monument?

49. A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]18^\circ[/latex], and that the angle of depression to the bottom of the tower is [latex]3^\circ[/latex]. How far is the person from the monument?

50. There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]40^\circ[/latex]. From the same location, the angle of elevation to the top of the antenna is measured to be [latex]43^\circ[/latex]. Find the height of the antenna.

51. There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]36^\circ[/latex]. From the same location, the angle of elevation to the top of the lightning rod is measured to be [latex]38^\circ[/latex]. Find the height of the lightning rod.

52. A 33-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ[/latex]. How high does the ladder reach up the side of the building?

53. A 23-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ[/latex]. How high does the ladder reach up the side of the building?

54. The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.

55. The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.

56. Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be [latex]60^\circ[/latex], how far from the base of the tree am I?

57. An airplane has only enough gas to fly to a city 200 miles northeast of its current location. If the pilot knows that the city is 25 miles north, how many degrees north of east should the airplane fly?

58. If a loading ramp is placed next to a truck, at a height of 4 feet, and the ramp is 15 feet long, what angle does the ramp make with the ground?

59. If a loading ramp is placed next to a truck, at a height of 2 feet, and the ramp is 20 feet long, what angle does the ramp make with the ground?

60. A woman is watching a launched rocket currently 11 miles in altitude. If she is standing 4 miles from the launch pad, at what angle is she looking up from horizontal?

61. An astronaut is in a launched rocket currently 15 miles in altitude. If a man is standing 2 miles from the launch pad, at what angle is she looking down at him from horizontal? (Hint: this is called the angle of depression.)

62. A woman is standing 8 meters away from a 10-meter tall building. At what angle is she looking to the top of the building?

63. A man is standing 10 meters away from a 6-meter tall building. Someone at the top of the building is looking down at him. At what angle is the person looking at him?

64. A 20-foot tall building has a shadow that is 55 feet long. What is the angle of elevation of the sun?

65. A 90-foot tall building has a shadow that is 2 feet long. What is the angle of elevation of the sun?

66. A spotlight on the ground 3 meters from a 2-meter tall man casts a 6 meter shadow on a wall 6 meters from the man. At what angle is the light?

67. A spotlight on the ground 3 feet from a 5-foot tall woman casts a 15-foot tall shadow on a wall 6 feet from the woman. At what angle is the light?

For the following exercises, find a solution to the following word problem algebraically. Then use a calculator to verify the result. Round the answer to the nearest tenth of a degree.

68. A person does a handstand with his feet touching a wall and his hands 1.5 feet away from the wall. If the person is 6 feet tall, what angle do his feet make with the wall?

69. A person does a handstand with her feet touching a wall and her hands 3 feet away from the wall. If the person is 5 feet tall, what angle do her feet make with the wall?

70. A 23-foot ladder is positioned next to a house. If the ladder slips at 7 feet from the house when there is not enough traction, what angle should the ladder make with the ground to avoid slipping?