Solving Right Triangle Problems

We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem. We begin with the familiar Pythagorean Theorem, [latex]{a}^{2}+{b}^{2}={c}^{2}[/latex], and model an equation to fit a situation.

Example 18: Using the Pythagorean Theorem to Model an Equation

Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.

One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)?

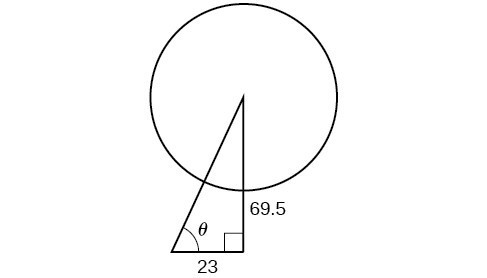
Basic diagram of a ferris wheel (circle) and its support cables (form a right triangle). One cable runs from the center of the circle to the ground (outside the circle), is perpendicular to the ground, and has length 69.5. Another cable of unknown length (the hypotenuse) runs from the center of the circle to the ground 23 feet away from the other cable at an angle of theta degrees with the ground. So, in closing, there is a right triangle with base 23, height 69.5, hypotenuse unknown, and angle between base and hypotenuse of theta degrees.

Figure 4

Solution

Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.

[latex]\begin{array}{l}\hfill \\ \begin{array}{l}\begin{array}{l}\hfill \\ \text{ }{a}^{2}+{b}^{2}={c}^{2}\hfill \end{array}\hfill \\ {\left(23\right)}^{2}+{\left(69.5\right)}^{2}\approx 5359\hfill \\ \text{ }\sqrt{5359}\approx 73.2\text{ m}\hfill \end{array}\hfill \end{array}[/latex]

The angle of elevation is [latex]\theta[/latex], formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.

[latex]\begin{array}{l}\hfill \\ \text{ }\tan \theta =\frac{69.5}{23}\hfill \\ \hfill \\ \hfill \\ {\tan }^{-1}\left(\frac{69.5}{23}\right)\approx 1.2522\hfill \\ \text{ }\approx {71.69}^{\circ }\hfill \end{array}[/latex]

The angle of elevation is approximately [latex]{71.7}^{\circ }[/latex], and the length of the cable is 73.2 meters.

Example 19: Using the Pythagorean Theorem to Model an Abstract Problem

OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.

Solution

For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “a” feet from the wall, the length of the ladder will be 4a feet.

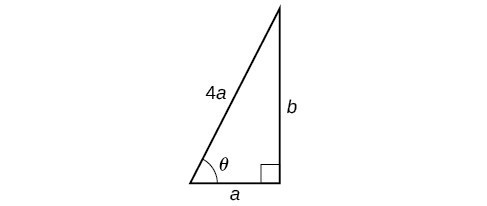
Diagram of a right triangle with base length a, height length b, hypotenuse length 4a. Opposite the height is an angle of theta degrees, and opposite the hypotenuse is an angle of 90 degrees.

Figure 5

The side adjacent to [latex]\theta[/latex] is a and the hypotenuse is [latex]4a[/latex]. Thus,

[latex]\begin{array}{l}\text{ }\cos \theta =\frac{a}{4a}=\frac{1}{4}\hfill \\ {\cos }^{-1}\left(\frac{1}{4}\right)\approx {75.5}^{\circ }\hfill \end{array}[/latex]

The elevation of the ladder forms an angle of [latex]{75.5}^{\circ }[/latex] with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:

[latex]\begin{array}{l}{a}^{2}+{b}^{2}={\left(4a\right)}^{2}\hfill \\ \text{ }{b}^{2}={\left(4a\right)}^{2}-{a}^{2}\hfill \\ \text{ }{b}^{2}=16{a}^{2}-{a}^{2}\hfill \\ \text{ }{b}^{2}=15{a}^{2}\hfill \\ \text{ }b=\sqrt{15}a\hfill \end{array}[/latex]

Thus, the ladder touches the wall at [latex]\sqrt{15}a[/latex] feet from the ground.