Learning Outcomes
- Describe the composition and function of acid–base buffers
- Calculate the pH of a buffer before and after the addition of added acid or base
A solution containing appreciable amounts of a weak conjugate acid-base pair is called a buffer solution, or a buffer. Buffer solutions resist a change in pH when small amounts of a strong acid or a strong base are added (Figure 1). A solution of acetic acid and sodium acetate (CH3COOH + CH3COONa) is an example of a buffer that consists of a weak acid and its salt. An example of a buffer that consists of a weak base and its salt is a solution of ammonia and ammonium chloride (NH3(aq) + NH4Cl(aq)).

Figure 1. (a) The unbuffered solution on the left and the buffered solution on the right have the same pH (pH 8); they are basic, showing the yellow color of the indicator methyl orange at this pH. (b) After the addition of 1 mL of a 0.01-M HCl solution, the buffered solution has not detectably changed its pH but the unbuffered solution has become acidic, as indicated by the change in color of the methyl orange, which turns red at a pH of about 4. (credit: modification of work by Mark Ott)
How Buffers Work
To illustrate the function of a buffer solution, consider a mixture of roughly equal amounts of acetic acid and sodium acetate. The presence of a weak conjugate acid-base pair in the solution imparts the ability to neutralize modest amounts of added strong acid or base. For example, adding strong base to this solution will neutralize hydronium ion and shift the acetic acid ionization equilibrium to the right, partially restoring the decreased H3O+ concentration:
[latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\leftrightharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)[/latex]
Likewise, adding strong acid to this buffer solution will neutralize acetate ion, shifting the above ionization equilibrium right and returning [H3O+] to near its original value. Figure 2 provides a graphical illustration of the changes in conjugate-partner concentration that occur in this buffer solution when strong acid and base are added. The buffering action of the solution is essentially a result of the added strong acid and base being converted to the weak acid and base that make up the buffer’s conjugate pair. The weaker acid and base undergo only slight ionization, as compared with the complete ionization of the strong acid and base, and the solution pH, therefore, changes much less drastically than it would in an unbuffered solution.
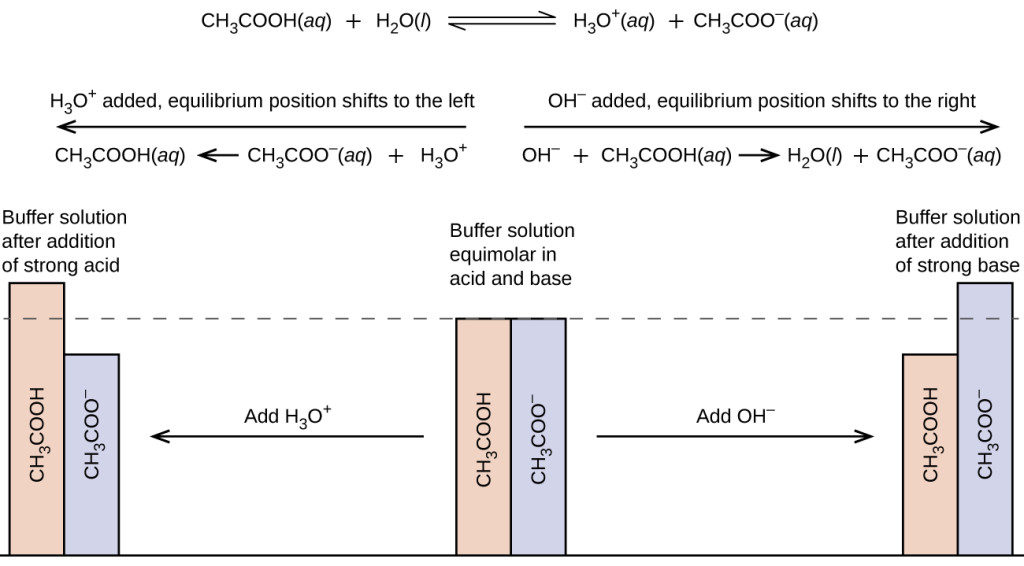
Figure 2. Buffering action in a mixture of acetic acid and acetate salt.
Example 1: pH Changes in Buffered and Unbuffered Solutions
Acetate buffers are used in biochemical studies of enzymes and other chemical components of cells to prevent pH changes that might affect the biochemical activity of these compounds.
(a) Calculate the pH of an acetate buffer that is a mixture with 0.10 M acetic acid and 0.10 M sodium acetate.
(b) Calculate the pH after 1.0 mL of 0.10 NaOH is added to 100 mL of this buffer.
(c) For comparison, calculate the pH after 1.0 mL of 0.10 M NaOH is added to 100 mL of a solution of an unbuffered solution with a pH of 4.74.
Part A
Show Solution
To determine the pH of the buffer solution we use a typical equilibrium calculation (as illustrated in earlier Examples):

Step 1. Determine the direction of change.
[latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)[/latex]
We look it up in Ionization Constants of Weak Acids: Ka = 1.8 [latex]\times[/latex] 10−5.
With [CH3CO2H] = [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] = 0.10 M and [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = ~0 M, the reaction shifts to the right to form [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex].
Step 2. Determine x and equilibrium concentrations. A table of changes and concentrations follows:![This table has two main columns and four rows. The first row for the first column does not have a heading and then has the following in the first column: Initial concentration ( M ), Change ( M ), Equilibrium concentration ( M ). The second column has the header of “[ C H subscript 3 C O subscript 2 H ] [ H subscript 2 O ] equilibrium arrow H subscript 3 O superscript plus sign [ C H subscript 3 C O subscript 2 superscript negative sign ].” Under the second column is a subgroup of four columns and three rows. The first column has the following: 0.10, negative x, 0.10 minus sign x. The second column is blank. The third column has the following: approximately 0, positive x, x. The fourth column has the following: 0.10, positive x, 0.10 plus sign x.](https://openstax.org/resources/c6cd395413486614bd489c119fd3913a299faa7e)
Step 3. Solve for x and the equilibrium concentrations.
[latex]x=1.8\times {10}^{-5}M[/latex]
[latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=0+x=1.8\times {10}^{-5}M[/latex]
[latex]\text{pH}=-\text{log}\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=-\text{log}\left(1.8\times {10}^{-5}\right)[/latex]
[latex]=4.74[/latex]
Step 4. Check the work. If we calculate all calculated equilibrium concentrations, we find that the equilibrium value of the reaction coefficient, Q = Ka.
Part B
Show Solution
Adding strong acid will neutralize some of the acetic acid, yielding the conjugate base acetate ion. Compute the new concentrations of these two buffer components, then repeat the equilibrium calculation of part (a) using these new concentrations.![Eight tan rectangles are shown in four columns of two rectangles each that are connected with right pointing arrows. The first rectangle in the upper left is labeled “Volume of N a O H solution.” An arrow points right to a second rectangle labeled “Moles of N a O H added.” A second arrow points right to a third rectangle labeled “Additional moles of N a C H subscript 3 C O subscript 2.” Just beneath the first rectangle in the upper left is a rectangle labeled “Volume of buffer solution.” An arrow points right to another rectangle labeled “Initial moles of C H subscript 3 C O subscript 2 H.” This rectangle points to the same third rectangle, which is labeled “ Additional moles of N a C H subscript 3 C O subscript 2.” An arrow points right to a rectangle labeled “ Unreacted moles of C H subscript 3 C O subscript 2 H.” An arrow points from this rectangle to a rectangle below labeled “[ C H subscript 3 C O subscript 2 H ].” An arrow extends below the “Additional moles of N a C H subscript 3 C O subscript 2” rectangle to a rectangle labeled “[ C H subscript 3 C O subscript 2 ].” This rectangle points right to the rectangle labeled “[ C H subscript 3 C O subscript 2 H ].”](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/219/2016/08/09043740/CNX_Chem_14_06_steps2_img.jpg)
Step 1. Determine the moles of NaOH. One milliliter (0.0010 L) of 0.10 M NaOH contains
[latex]0.0010\cancel{\text{L}}\times \left(\dfrac{0.10\text{mol NaOH}}{1\cancel{\text{L}}}\right)=1.0\times {10}^{-4}\text{mol NaOH}[/latex]
Step 2. Determine the moles of CH2CO2H. Before reaction, 0.100 L of the buffer solution contains
[latex]0.100\cancel{\text{L}}\times \left(\dfrac{0.100\text{mol}{\text{ CH}}_{3}{\text{CO}}_{2}\text{H}}{1\cancel{\text{L}}}\right)=1.00\times {10}^{-2}\text{mol}{\text{CH}}_{3}{\text{CO}}_{2}\text{H}[/latex]
Step 3. Solve for the amount of NaCH3CO2 produced. The 1.0 [latex]\times[/latex] 10−4 mol of NaOH neutralizes 1.0 [latex]\times[/latex] 10−4 mol of CH3CO2H, leaving
[latex]\left(1.0\times {10}^{-2}\right)-\left(0.01\times {10}^{-2}\right)=0.99\times {10}^{-2}\text{mol}{\text{CH}}_{3}{\text{CO}}_{2}\text{H}[/latex]
and producing 1.0 [latex]\times[/latex] 10−4 mol of NaCH3CO2. This makes a total of
[latex]\left(1.0\times {10}^{-2}\right)+\left(0.01\times {10}^{-2}\right)=1.01\times {10}^{-2}\text{mol}{\text{NaCH}}_{3}{\text{CO}}_{2}[/latex]
Step 4. Find the molarity of the products. After reaction, CH3CO2H and NaCH3CO2 are contained in 101 mL of the intermediate solution, so:
[latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]=\dfrac{9.9\times {10}^{-3}\text{mol}}{0.101\text{L}}=0.098M[/latex]
[latex]\left[{\text{NaCH}}_{3}{\text{CO}}_{2}\right]=\dfrac{1.01\times {10}^{-2}\text{mol}}{0.101\text{L}}=0.100M[/latex]
Now we calculate the pH after the intermediate solution, which is 0.098 M in CH3CO2H and 0.100 M in NaCH3CO2, comes to equilibrium. The calculation is very similar to that in part (a) of this example:
 This series of calculations gives a pH = 4.75. Thus the addition of the base barely changes the pH of the solution (F).
This series of calculations gives a pH = 4.75. Thus the addition of the base barely changes the pH of the solution (F).
Part C
Show Solution
This 1.8 [latex]\times[/latex] 10−5–M solution of HCl has the same hydronium ion concentration as the 0.10-M solution of acetic acid-sodium acetate buffer described in part (a) of this example. The solution contains:
[latex]0.100\text{L}\times \left(\dfrac{1.8\times {10}^{-5}\text{mol HCl}}{1\text{L}}\right)=1.8\times {10}^{-6}\text{mol HCl}[/latex]
As shown in part (b), 1 mL of 0.10 M NaOH contains 1.0 [latex]\times[/latex] 10−4 mol of NaOH. When the NaOH and HCl solutions are mixed, the HCl is the limiting reagent in the reaction. All of the HCl reacts, and the amount of NaOH that remains is:
[latex]\left(1.0\times {10}^{-4}\right)-\left(1.8\times {10}^{-6}\right)=9.8\times {10}^{-5}M[/latex]
- The concentration of NaOH is: [latex]\dfrac{9.8\times {10}^{-5}M\text{NaOH}}{0.101\text{L}}=9.7\times {10}^{-4}M[/latex]
- The pOH of this solution is: [latex]\text{pOH}=-\text{log}\left[{\text{OH}}^{-}\right]=-\text{log}\left(9.7\times {10}^{-4}\right)=3.01[/latex]
- The pH is: [latex]\text{pH}=14.00-\text{pOH}=10.99[/latex]
The pH changes from 4.74 to 10.99 in this unbuffered solution. This compares to the change of 4.74 to 4.75 that occurred when the same amount of NaOH was added to the buffered solution described in part (b).
Check Your Learning
Show that adding 1.0 mL of 0.10 M HCl changes the pH of 100 mL of a 1.8 [latex]\times[/latex] 10−5M HCl solution from 4.74 to 3.00.
Show Solution
Initial pH of 1.8 [latex]\times[/latex] 10−5M HCl; pH = −log [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = −log[1.8 [latex]\times[/latex] 10−5] = 4.74
Moles of [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] in 100 mL 1.8 [latex]\times[/latex] 10−5M HCl; 1.8 [latex]\times[/latex] 10−5 moles/L [latex]\times[/latex] 0.100 L = 1.8 [latex]\times[/latex] 10−6
Moles of [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] added by addition of 1.0 mL of 0.10 M HCl: 0.10 moles/L [latex]\times[/latex] 0.0010 L = 1.0 [latex]\times[/latex] 10−4 moles; final pH after addition of 1.0 mL of 0.10 M HCl:
[latex]\text{pH}=-\text{log}\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=-\text{log}\left(\dfrac{\text{total moles}{\text{ H}}_{3}{\text{O}}^{\text{+}}}{\text{total volume}}\right)=-\text{log}\left(\dfrac{1.0\times {10}^{-4}\text{mol}+1.8\times {10}^{-6}\text{mol}}{101\text{mL}\left(\frac{1\text{L}}{1000\text{mL}}\right)}\right)=3.00[/latex]
If we add an acid or a base to a buffer that is a mixture of a weak base and its salt, the calculations of the changes in pH are analogous to those for a buffer mixture of a weak acid and its salt.
Buffer Capacity
Buffer solutions do not have an unlimited capacity to keep the pH relatively constant (Figure 3). If we add so much base to a buffer that the weak acid is exhausted, no more buffering action toward the base is possible. On the other hand, if we add an excess of acid, the weak base would be exhausted, and no more buffering action toward any additional acid would be possible. In fact, we do not even need to exhaust all of the acid or base in a buffer to overwhelm it; its buffering action will diminish rapidly as a given component nears depletion.

Figure 3. The indicator color (methyl orange) shows that a small amount of acid added to a buffered solution of pH 8 (beaker on the left) has little affect on the buffered system (middle beaker). However, a large amount of acid exhausts the buffering capacity of the solution and the pH changes dramatically (beaker on the right). (credit: modification of work by Mark Ott)
The buffer capacity is the amount of acid or base that can be added to a given volume of a buffer solution before the pH changes significantly, usually by one unit. Buffer capacity depends on the amounts of the weak acid and its conjugate base that are in a buffer mixture. For example, 1 L of a solution that is 1.0 M in acetic acid and 1.0 M in sodium acetate has a greater buffer capacity than 1 L of a solution that is 0.10 M in acetic acid and 0.10 M in sodium acetate even though both solutions have the same pH. The first solution has more buffer capacity because it contains more acetic acid and acetate ion.
Selection of Suitable Buffer Mixtures
There are two useful rules of thumb for selecting buffer mixtures:
- A good buffer mixture should have about equal concentrations of both of its components. A buffer solution has generally lost its usefulness when one component of the buffer pair is less than about 10% of the other. Figure 4 shows an acetic acid-acetate ion buffer as base is added. The initial pH is 4.74. A change of 1 pH unit occurs when the acetic acid concentration is reduced to 11% of the acetate ion concentration.
![A graph is shown with a horizontal axis labeled “Added m L of 0.10 M N a O H” which has markings and vertical gridlines every 10 units from 0 to 110. The vertical axis is labeled “p H” and is marked every 1 unit beginning at 0 extending to 11. A break is shown in the vertical axis between 0 and 4. A red curve is drawn on the graph which increases gradually from the point (0, 4.8) up to about (100, 7) after which the graph has a vertical section up to about (100, 11). The curve is labeled [ C H subscript 3 C O subscript 2 H ] is 11 percent of [ C H subscript 3 CO subscript 2 superscript negative].](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/219/2016/08/09044040/CNX_Chem_14_06_buffer.jpg)
Figure 4. The graph, an illustration of buffering action, shows change of pH as an increasing amount of a 0.10-M NaOH solution is added to 100 mL of a buffer solution in which, initially, [CH3CO2H] = 0.10 M and [CH3CO2−]=0.10M. Note the greatly diminished buffering action occurring after the buffer capacity has been reached, resulting in drastic rises in pH on adding more strong base.
- Weak acids and their salts are better as buffers for pHs less than 7; weak bases and their salts are better as buffers for pHs greater than 7.
Blood is an important example of a buffered solution, with the principal acid and ion responsible for the buffering action being carbonic acid, H2CO3, and the bicarbonate ion, [latex]{\text{HCO}}_{3}{}^{-}[/latex]. When an excess of hydrogen ion enters the blood stream, it is removed primarily by the reaction:
[latex]{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{HCO}}_{3}{}^{-}\left(aq\right)\longrightarrow {\text{H}}_{2}{\text{CO}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)[/latex]
When an excess of the hydroxide ion is present, it is removed by the reaction:
[latex]{\text{OH}}^{-}\left(aq\right)+{\text{H}}_{2}{\text{CO}}_{3}\left(aq\right)\longrightarrow {\text{HCO}}_{3}{}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)[/latex]
The added strong acid or base is thus effectively converted to the much weaker acid or base of the buffer pair (H3O+ is converted to H2CO3 and OH– is converted to HCO3–). The pH of human blood thus remains very near the value determined by the buffer pairs pKa, in this case, 7.35. Normal variations in blood pH are usually less than 0.1, and pH changes of 0.4 or greater are likely to be fatal.
The Henderson-Hasselbalch Equation
The ionization-constant expression for a solution of a weak acid can be written as:
[latex]{K}_{\text{a}}=\dfrac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{A}}^{-}\right]}{\text{[HA]}}[/latex]
Rearranging to solve for [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex], we get:
[latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]={K}_{\text{a}}\times \dfrac{\text{[HA]}}{\left[{\text{A}}^{-}\right]}[/latex]
Taking the negative logarithm of both sides of this equation, we arrive at:
[latex]-\text{log}\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]=-\text{log}{K}_{\text{a}}\text{- log}\dfrac{\left[\text{HA}\right]}{\left[{\text{A}}^{-}\right]}[/latex],
which can be written as
[latex]\text{pH}=\text{p}{K}_{\text{a}}+\text{log}\dfrac{\left[{\text{A}}^{-}\right]}{\left[\text{HA}\right]}[/latex]
where pKa is the negative of the common logarithm of the ionization constant of the weak acid (pKa = −log Ka). This equation relates the pH, the ionization constant of a weak acid, and the concentrations of the weak acid and its salt in a buffered solution. Scientists often use this expression, called the Henderson-Hasselbalch equation, to calculate the pH of buffer solutions. It is important to note that the “x is small” assumption must be valid to use this equation.
Lawrence Joseph Henderson and Karl Albert Hasselbalch
Lawrence Joseph Henderson (1878–1942) was an American physician, biochemist and physiologist, to name only a few of his many pursuits. He obtained a medical degree from Harvard and then spent 2 years studying in Strasbourg, then a part of Germany, before returning to take a lecturer position at Harvard. He eventually became a professor at Harvard and worked there his entire life. He discovered that the acid-base balance in human blood is regulated by a buffer system formed by the dissolved carbon dioxide in blood. He wrote an equation in 1908 to describe the carbonic acid-carbonate buffer system in blood. Henderson was broadly knowledgeable; in addition to his important research on the physiology of blood, he also wrote on the adaptations of organisms and their fit with their environments, on sociology and on university education. He also founded the Fatigue Laboratory, at the Harvard Business School, which examined human physiology with specific focus on work in industry, exercise, and nutrition.
In 1916, Karl Albert Hasselbalch (1874–1962), a Danish physician and chemist, shared authorship in a paper with Christian Bohr in 1904 that described the Bohr effect, which showed that the ability of hemoglobin in the blood to bind with oxygen was inversely related to the acidity of the blood and the concentration of carbon dioxide. The pH scale was introduced in 1909 by another Dane, Sørensen, and in 1912, Hasselbalch published measurements of the pH of blood. In 1916, Hasselbalch expressed Henderson’s equation in logarithmic terms, consistent with the logarithmic scale of pH, and thus the Henderson-Hasselbalch equation was born.
Medicine: The Buffer System in Blood
The normal pH of human blood is about 7.4. The carbonate buffer system in the blood uses the following equilibrium reaction:
[latex]{\text{CO}}_{2}\left(g\right)+2{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{2}{\text{CO}}_{3}\left(aq\right)\rightleftharpoons {\text{HCO}}_{3}{}^{-}\left(aq\right)+{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)[/latex]
The concentration of carbonic acid, H2CO3 is approximately 0.0012 M, and the concentration of the hydrogen carbonate ion, [latex]{\text{HCO}}_{3}{}^{-}[/latex], is around 0.024 M. Using the Henderson-Hasselbalch equation and the pKa of carbonic acid at body temperature, we can calculate the pH of blood:
[latex]\text{pH}=\text{p}{K}_{\text{a}}+\text{log}\dfrac{\left[\text{base}\right]}{\left[\text{acid}\right]}=6.1+\text{log}\dfrac{0.024}{0.0012}=7.4[/latex]
The fact that the H2CO3 concentration is significantly lower than that of the [latex]{\text{HCO}}_{3}{}^{-}[/latex] ion may seem unusual, but this imbalance is due to the fact that most of the by-products of our metabolism that enter our bloodstream are acidic. Therefore, there must be a larger proportion of base than acid, so that the capacity of the buffer will not be exceeded.
Lactic acid is produced in our muscles when we exercise. As the lactic acid enters the bloodstream, it is neutralized by the [latex]{\text{HCO}}_{3}{}^{-}[/latex] ion, producing H2CO3. An enzyme then accelerates the breakdown of the excess carbonic acid to carbon dioxide and water, which can be eliminated by breathing. In fact, in addition to the regulating effects of the carbonate buffering system on the pH of blood, the body uses breathing to regulate blood pH. If the pH of the blood decreases too far, an increase in breathing removes CO2 from the blood through the lungs driving the equilibrium reaction such that [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] is lowered. If the blood is too alkaline, a lower breath rate increases CO2 concentration in the blood, driving the equilibrium reaction the other way, increasing [H+] and restoring an appropriate pH.
Key Concepts and Summary
Solutions that contain appreciable amounts of a weak conjugate acid-base pair are called buffers. A buffered solution will experience only slight changes in pH when small amounts of acid or base are added. Addition of large amounts of acid or base can exceed the buffer capacity, consuming most of one conjugate partner and preventing further buffering action.
Key Equations
- [latex]\text{p}K_{\text{a}}=−\text{log}K_{\text{a}}[/latex]
- [latex]\text{p}K_{\text{b}}=−\text{log}K_{\text{b}}[/latex]
- [latex]\text{pH}=\text{p}{K}_{\text{a}}+\text{log}\dfrac{\left[{\text{A}}^{-}\right]}{\left[\text{HA}\right]}[/latex]
Try It
- Explain why a buffer can be prepared from a mixture of NH4Cl and NaOH but not from NH3 and NaOH.
- Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the acid H3PO4 and a salt of its conjugate base NaH2PO4.
- Explain why the pH does not change significantly when a small amount of an acid or a base is added to a solution that contains equal amounts of the base NH3 and a salt of its conjugate acid NH4Cl.
- What is [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] in a solution of 0.25 M CH3CO2H and 0.030 M NaCH3CO2?
[latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right){K}_{\text{a}}=1.8\times {10}^{-5}[/latex]
- What is [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] in a solution of 0.075 M HNO2 and 0.030 M NaNO2?
[latex]{\text{HNO}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{NO}}_{2}{}^{-}\left(aq\right){K}_{\text{a}}=4.5\times {10}^{-5}[/latex]
- What is [OH−] in a solution of 0.125 M CH3NH2 and 0.130 M CH3NH3Cl?
[latex]{\text{CH}}_{3}{\text{NH}}_{2}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{CH}}_{3}{\text{NH}}_{3}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right){K}_{\text{b}}=4.4\times {10}^{-4}[/latex]
- What is [OH−] in a solution of 1.25 M NH3 and 0.78 M NH4NO3?
[latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right){K}_{\text{b}}=1.8\times {10}^{-5}[/latex]
- What concentration of NH4NO3 is required to make [OH−] = 1.0 [latex]\times[/latex] 10−5 in a 0.200-M solution of NH3?
- What concentration of NaF is required to make [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 2.3 [latex]\times[/latex] 10−4 in a 0.300-M solution of HF?
- What is the effect on the concentration of acetic acid, hydronium ion, and acetate ion when the following are added to an acidic buffer solution of equal concentrations of acetic acid and sodium acetate:
- HCl
- KCH3CO2
- NaCl
- KOH
- CH3CO2H
- What is the effect on the concentration of ammonia, hydroxide ion, and ammonium ion when the following are added to a basic buffer solution of equal concentrations of ammonia and ammonium nitrate:
- KI
- NH3
- HI
- NaOH
- NH4Cl
- What will be the pH of a buffer solution prepared from 0.20 mol NH3, 0.40 mol NH4NO3, and just enough water to give 1.00 L of solution?
- Calculate the pH of a buffer solution prepared from 0.155 mol of phosphoric acid, 0.250 mole of KH2PO4, and enough water to make 0.500 L of solution.
- How much solid NaCH3CO2•3H2O must be added to 0.300 L of a 0.50-M acetic acid solution to give a buffer with a pH of 5.00? (Hint: Assume a negligible change in volume as the solid is added.)
- What mass of NH4Cl must be added to 0.750 L of a 0.100-M solution of NH3 to give a buffer solution with a pH of 9.26? (Hint: Assume a negligible change in volume as the solid is added.)
Show Selected Solutions
2. Excess [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] is removed primarily by the reaction [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{H}}_{2}{\text{PO}}_{4}{}^{-}\left(aq\right)\longrightarrow {\text{H}}_{3}{\text{PO}}_{4}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)[/latex]
Excess base is removed by the reaction [latex]{\text{OH}}^{-}\left(aq\right)+{\text{H}}_{3}{\text{PO}}_{4}\left(aq\right)\longrightarrow {\text{H}}_{2}{\text{PO}}_{4}{}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)[/latex]
4. The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=1.8\times {10}^{-5}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
|
[CH3CO2H] |
[H3O+] |
[CH3CO2] |
| Initial concentration (M) |
0.25 |
0 |
0.030 |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.25 − x |
x |
0.030 + x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumptions that (0.25 − x) ≈ 0.25 and (0.030 − x) ≈ 0.030, gives:
[latex]\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\frac{\left(x\right)\left(0.030-x\right)}{\left(0.25-x\right)}\approx \frac{\left(x\right)\left(0.030\right)}{0.25}=1.8\times {10}^{-5}[/latex]
Solving for x gives 1.50 [latex]\times[/latex] 10−4M. Because this value is less than 5% of both 0.25 and 0.030, our assumptions are correct. Therefore, [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 1.5 [latex]\times[/latex] 10−4M.
This problem can also be solved using the Henderson-Hasselbalch equation: [latex]\text{pH}=\text{p}{K}_{\text{a}}+\text{log}\frac{\left[{\text{A}}^{-}\right]}{\left[\text{HA}\right]}[/latex]; pKa = −log(Ka) = −log(1.8 [latex]\times[/latex] 10−5) = 4.74; [HA] ≈ [HA]0 = [CH3CO2H]0 = 0.25 M; [A−] ≈ [NaCH3CO2] = 0.030 M. Using these data: [latex]\text{pH}=4.74-\text{log}\left(\frac{0.030M}{0.25M}\right)=3.82[/latex]; [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 10−pHM = 10−3.82M = 1.5 [latex]\times[/latex] 10−4M
6. The equilibrium expression is: [latex]{K}_{\text{b}}=\frac{\left[{\text{CH}}_{3}{\text{NH}}_{3}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{CH}}_{3}{\text{NH}}_{2}\right]}=4.4\times {10}^{-4}[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
|
[CH3NH2] |
[CH3NH3+] |
[OH−] |
| Initial concentration (M) |
0.125 |
0.130 |
0 |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.125 − x |
0.130 + x |
x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumptions that (0.125 − x) ≈ 0.125 and (0.130 − x) ≈ 0.130, gives:
[latex]\frac{\left[{\text{CH}}_{3}{\text{NH}}_{3}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{CH}}_{3}{\text{NH}}_{2}\right]}=\frac{\left(0.130-x\right)\left(x\right)}{\left(0.125-x\right)}\approx \frac{\left(0.130\right)\left(x\right)}{0.125}=4.4\times {10}^{-4}[/latex]
Solving for x gives 4.23 [latex]\times[/latex] 10−4M. Because this value is less than 5% of both 0.125 and 0.130, our assumptions are correct. Therefore, [OH−] = 4.2 [latex]\times[/latex] 10−4M.
8. The reaction and equilibrium constant are [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\,\,\,\,\,\,\,\,\,\,\,{K}_{\text{b}}=1.8\times {10}^{-4}[/latex]
The equilibrium expression is [latex]{K}_{\text{b}}=\frac{\left[{\text{NH}}_{4}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=1.8\times {10}^{-5}[/latex]
Let x = the concentration of NH4NO3 required. The initial and equilibrium concentrations for this system can be written as follows:
|
[NH3] |
[NH4+] |
[OH−] |
| Initial concentration (M) |
0.200 |
0.78 |
0 |
| Change (M) |
−x |
x + x |
x |
| Equilibrium (M) |
0.200 − x |
x + x |
x = 1.0 × 10−5 |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumption that (x + x) ≈ x, gives:
[latex]\frac{\left[{\text{NH}}_{4}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=\frac{\left(x-x\right)\left(1.0\times {10}^{-5}\right)}{\left(0.200 - 1.0\times {10}^{-5}\right)}\approx \frac{\left(x\right)\left(1.0\times {10}^{-5}\right)}{0.200}=1.8\times {10}^{-5}[/latex]
Solving for x gives 0.360 M. Because x is less than 5% of this value, our assumption is correct. Therefore, [latex]\left[{\text{NH}}_{4}{}^{\text{+}}\right][/latex] = [NH4NO3] = 0.36 M.
10. The reaction and equilibrium constant are [latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)\,\,\,\,\,\,\,\,\,\,\,{K}_{\text{a}}=1.8\times {10}^{-5}[/latex]
- (a) The added HCl will increase the concentration of [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] slightly, which will react with [latex]{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}[/latex] and produce CH3CO2H in the process. Thus, [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] decreases and [CH3CO2H] increases.
- (b) The added KCH3CO2 will increase the concentration of [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] which will react with [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] and produce CH3CO2 H in the process. Thus, [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] decreases slightly and [CH3CO2H] increases.
- (c) The added NaCl will have no effect on the concentration of the ions.
- (d) The added KOH will produce OH− ions, which will react with the [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex], thus reducing [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex]. Some additional CH3CO2H will dissociate, producing [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] ions in the process. Thus, [CH3CO2H] decreases slightly and [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] increases.
- (e) The added CH3CO2H will increase its concentration, causing more of it to dissociate and producing more [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] and [latex]{\text{H}}_{3}{\text{O}}^{\text{+}}[/latex] in the process. Thus, [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] increases slightly and [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] increases.
12. The reaction and equilibrium constant are: [latex]{\text{NH}}_{3}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{NH}}_{4}{}^{\text{+}}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\,\,\,\,\,\,\,\,\,\,\,{K}_{\text{b}}=1.8\times {10}^{-5}[/latex]
The equilibrium expression is: [latex]{K}_{\text{b}}=\frac{\left[{\text{NH}}_{4}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=1.8\times {10}^{-5}[/latex]
The initial concentrations of NH3 and [latex]{\text{NH}}_{4}{}^{\text{+}}[/latex] are 0.20 M and 0.40 M, respectively. The equilibrium concentrations for this system can be written as follows:
|
[NH3] |
NH4+] |
[OH−] |
| Initial concentration (M) |
0.20 |
0.40 |
0 |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.20 − x |
0.40 + x |
x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumptions that (0.20 − x) ≈ 0.20 and (0.40 + x) ≈ 0.40, gives:
[latex]\frac{\left[{\text{NH}}_{4}{}^{\text{+}}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{NH}}_{3}\right]}=\frac{\left(0.40+x\right)\left(x\right)}{\left(0.20-x\right)}\approx \frac{\left(0.40\right)\left(x\right)}{0.20}=1.8\times {10}^{-5}[/latex]
Solving for x gives 9.00 [latex]\times[/latex] 10−6M. Because this value is less than 5% of both 0.20 and 0.40, our assumptions are correct. Therefore, [OH−] = 9.00 [latex]\times[/latex] 10−6M. Thus:
- pOH = −log(9.00 [latex]\times[/latex] 10−6) = 5.046
- pH = 14.000 − pOH = 14.000 − 5.046 = 8.954 = 8.95
14. The reaction and equilibrium constant are: [latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)\,\,\,\,\,\,\,\,\,\,\,{K}_{\text{a}}=1.8\times {10}^{-5}[/latex]
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=1.8\times {10}^{-5}[/latex]
Let x be the concentration of [latex]{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}[/latex]. The hydronium ion concentration at equilibrium is [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 10−pH = 10−5.00 = 1.00 [latex]\times[/latex] 10−5M
The initial and equilibrium concentrations for this system can be written as follows:
|
[CH3CO2H] |
[H3O+] |
[CH3CO2] |
| Initial concentration (M) |
0.50 |
0 |
x |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.50 − x |
x = 10 × 10−5 |
x + x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumption that (x + x) ≈ x, gives:
[latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\frac{\left(1.0\times {10}^{-5}\right)\left(x+x\right)}{\left(0.50 - 1.0\times {10}^{-5}\right)}\approx \frac{\left(1.0\times {10}^{-5}\right)\left(x\right)}{0.50}=1.8\times {10}^{-5}[/latex]
Solving for x gives 0.900 M. Because x is less than 5% of this value, our assumption is correct. Therefore, [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right][/latex] = 0.900 M. Using the molar mass of NaC2H3O2•3H2O (136.080 /mol) and the volume gives the mass required:
[latex]\frac{0.900\text{mol}}{1\text{L}}\times 0.300\text{L}\times \frac{136.080\text{g}}{1\text{mol}}=36.7=37\text{g}\left(0.27\text{mol}\right)[/latex]
Try It
- A buffer solution is prepared from equal volumes of 0.200 M acetic acid and 0.600 M sodium acetate. Use 1.80 × 10−5 as Ka for acetic acid.
- What is the pH of the solution?
- Is the solution acidic or basic?
- What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to 0.200 L of the original buffer?
- A 5.36–g sample of NH4Cl was added to 25.0 mL of 1.00 M NaOH and the resulting solution diluted to 0.100 L.
- What is the pH of this buffer solution?
- Is the solution acidic or basic?
- What is the pH of a solution that results when 3.00 mL of 0.034 M HCl is added to the solution?
Show Solution to Question 1
Part A
The reaction and equilibrium constant are [latex]{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons {\text{H}}_{3}{\text{O}}^{\text{+}}\left(aq\right)+{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\left(aq\right)\,\,\,\,\,\,\,\,\,\,\,{K}_{\text{a}}=1.8\times {10}^{-5}[/latex]
The equilibrium expression is [latex]{K}_{\text{a}}=\frac{\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=1.8\times {10}^{-5}[/latex]
The molar mass of NH4Cl is 53.4912 g/mol. The moles of NH4Cl are: [latex]\frac{5.36\text{g}}{53.4912\text{g}{\text{mol}}^{-1}}=0.1002\text{mol}[/latex]
Assume 0.500 L of each solution is present The total volume is thus 1.000 L. The initial concentrations of the ions is obtained using M1V1 = M2V2, or:
[latex]\begin{array}{l} \left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]={M}_{1}\times \frac{{V}_{1}}{{V}_{2}}=\left(0.200\right)\times \frac{0.500\text{L}}{1.000\text{L}}=0.100M\\ \left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]={M}_{1}\times \frac{{V}_{1}}{{V}_{2}}=\left(0.600\right)\times \frac{0.500\text{L}}{1.000\text{L}}=0.300M\end{array}[/latex]
The initial and equilibrium concentrations of this system can be written as follows:
|
[CH3CO2H] |
[H3O+] |
[CH3CO2−] |
| Initial concentration (M) |
0.100 |
0 |
0.300 |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.100 − x |
x |
0.300 + x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumptions that (0.100 − x) ≈ 0.100 and (0.300 − x) ≈ 0.300, gives:
[latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\frac{\left(x\right)\left(0.300+x\right)}{\left(0.100-x\right)}\approx \frac{\left(x\right)\left(0.300\right)}{0.100}=1.80\times {10}^{-5}[/latex]
Solving for x gives 6.000 [latex]\times[/latex] 10−6M. Because this value is less than 5% of both 0.100 and 0.300, our assumptions are correct. Therefore [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 6.000 [latex]\times[/latex] 10−6M:
pH = −log(6.000 [latex]\times[/latex] 10−6) = 5.2218 = 5.222;
Part B
The solution is acidic.
Part C
Assume that the added H+ reacts completely with an equal amount of [latex]{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}[/latex], forming an equal amount of CH3CO2H in the process. The moles of H+ added equal 0.034 M [latex]\times[/latex] 0.00300 L = 1.02 [latex]\times[/latex] 10−4 mol. For the acetic acid, the initial moles present equal 0.2000 M [latex]\times[/latex] 0.500 L = 0.1000 mol, and for acetate ion, 0.600 M [latex]\times[/latex] 0.500 L = 0.3000 mol. Thus:
mol CH3CO2H = 0.1000 + 1.02 [latex]\times[/latex] 10−4 = 0.1001 mol
[latex]\text{mol}{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}=0.3000 - 1.02\times {10}^{-4}=0.2999\text{mol}[/latex]
Final volume = 1.000 L + 3.00 [latex]\times[/latex] 10−3 L = 1.0030 L
The initial concentrations are therefore:
- [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]=\frac{0.1001\text{mol}}{1.0030\text{L}}=0.09980M[/latex]
- [latex]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]=\frac{0.2999\text{mol}}{1.0030\text{L}}=0.2990M[/latex]
The initial and equilibrium concentrations for this system can be written as follows:
|
[CH3CO2H] |
[H3O+] |
[CH3CO2−] |
| Initial concentration (M) |
0.09980 |
0 |
0.2990 |
| Change (M) |
−x |
x |
x |
| Equilibrium (M) |
0.09980 − x |
x |
0.2990 + x |
Substituting the equilibrium concentrations into the equilibrium expression, and making the assumptions that (0.09980 − x) ≈ 0.09980 and (0.2990 − x) ≈ 0.2990, gives:
[latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]\left[{\text{CH}}_{3}{\text{CO}}_{2}{}^{-}\right]}{\left[{\text{CH}}_{3}{\text{CO}}_{2}\text{H}\right]}=\frac{\left(x\right)\left(0.2990+x\right)}{\left(0.09980-x\right)}\approx \frac{\left(x\right)\left(0.2990\right)}{0.09980}=1.80\times {10}^{-5}[/latex]
Solving for x gives 6.008 [latex]\times[/latex] 10−6M. Because this value is less than 5% of both 0.09980 and 0.2990, our assumptions are correct. Therefore, [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 6.008 [latex]\times[/latex] 10−6M.
pH = −log(6.008 [latex]\times[/latex] 10−6) = 5.2213 = 5.221
Try It
- Which acid in Table 1 of Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of 3.1? Explain your choice.
- Which acid in Table 1 of Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of 3.7? Explain your choice.
- Which base in Table 2 of Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of 10.65? Explain your choice.
- Which base in Table 2 of Relative Strengths of Acids and Bases is most appropriate for preparation of a buffer solution with a pH of 9.20? Explain your choice.
- Saccharin, C7H4NSO3H, is a weak acid (Ka = 2.1 [latex]\times[/latex] 10−2). If 0.250 L of diet cola with a buffered pH of 5.48 was prepared from 2.00 [latex]\times[/latex] 10−3 g of sodium saccharide, Na(C7H4NSO3), what are the final concentrations of saccharine and sodium saccharide in the solution?
- What is the pH of 1.000 L of a solution of 100.0 g of glutamic acid (C5H9NO4, a diprotic acid; K1 = 8.5 [latex]\times[/latex] 10−5, K2 = 3.39 [latex]\times[/latex] 10−10) to which has been added 20.0 g of NaOH during the preparation of monosodium glutamate, the flavoring agent? What is the pH when exactly 1 mol of NaOH per mole of acid has been added?
Show Selected Solutions
1. To prepare the best buffer for a weak acid HA and its salt, the ratio [latex]\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{{K}_{\text{a}}}[/latex] should be as close to 1 as possible for effective buffer action. The [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] concentration in a buffer of pH 3.1 is [latex]\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right][/latex] = 10−3.1 = 7.94 [latex]\times[/latex] 10−4M
We can now solve for Ka of the best acid as follows:
[latex]\begin{array}{l}{ }\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{{K}_{\text{a}}}=1\\ {K}_{\text{a}}=\frac{\left[{\text{H}}_{3}{\text{O}}^{\text{+}}\right]}{1}=7.94\times {10}^{-4}\end{array}[/latex]
In Table 1 of Relative Strengths of Acids and Bases, the acid with the closest Ka to 7.94 [latex]\times[/latex] 10−4 is HF, with a Ka of 7.2 [latex]\times[/latex] 10−4.
3. For buffers with pHs > 7, you should use a weak base and its salt. The most effective buffer will have a ratio [latex]\frac{\left[{\text{OH}}^{-}\right]}{{K}_{\text{b}}}[/latex] that is as close to 1 as possible. The pOH of the buffer is 14.00 − 10.65 = 3.35. Therefore, [OH−] is [OH−] = 10−pOH = 10−3.35 = 4.467 [latex]\times[/latex] 10−4M.
We can now solve for Kb of the best base as follows:
[latex]\frac{\left[{\text{OH}}^{-}\right]}{{K}_{\text{b}}}=1[/latex]
Kb = [OH−] = 4.47 [latex]\times[/latex] 10−4
In Table 2 of Relative Strengths of Acids and Bases, the base with the closest Kb to 4.47 [latex]\times[/latex] 10−4 is CH3NH2, with a Kb = 4.4 [latex]\times[/latex] 10−4.
5. The molar mass of sodium saccharide is 205.169 g/mol. Using the abbreviations HA for saccharin and NaA for sodium saccharide the number of moles of NaA in the solution is: [latex]2.00\times {10}^{-3}\text{g}\times \frac{1\text{mol}}{205.169\text{g}}=9.75\times {10}^{-6}\text{mol}[/latex]
This ionizes initially to form saccharin ions, A−, with:
[latex]\left[{\text{A}}^{-}\right]=\frac{9.75\times {10}^{-6}\text{mol}}{0.250\text{L}}=3.9\times {10}^{-5}M[/latex]
but A− reacts with water:
[latex]\begin{array}{l}{\text{A}}^{-}\left(aq\right)+{\text{H}}_{2}\text{O}\left(l\right)\rightleftharpoons \text{HA}\left(aq\right)+{\text{OH}}^{-}\left(aq\right)\\ {K}_{\text{b}}=\frac{{K}_{\text{w}}}{{K}_{\text{a}}}=\frac{1.0\times {10}^{-14}}{2.1\times {10}^{-12}}=4.8\times {10}^{-3}\\ =4.8\times {10}^{-3}=\frac{\left[\text{HA}\right]\left[{\text{OH}}^{-}\right]}{\left[{\text{A}}^{-}\right]}\end{array}[/latex]
The pH of the solution is 5.48, so pOH = 14.00 − 5.48 = 8.52, and [OH−] = 10−8.52 = 3.02 [latex]\times[/latex] 10−9M
Because of the small size of Kb, almost all the A− will be in the form of HA. Therefore, [latex]4.8\times {10}^{-3}=\frac{x\left(3.02\times {10}^{-9}\right)}{3.9\times {10}^{-5}-x}[/latex], where x ≈ 3.9 [latex]\times[/latex] 10−5M = [HA] = [C7H4NSO3H]
Consequently, [A−] is extremely small. Therefore, solve for [A−] from the equilibrium expression:
[latex]\left[{\text{A}}^{-}\right]=\frac{\left[\text{HA}\right]\left[{\text{OH}}^{-}\right]}{{K}_{\text{b}}}=\frac{\left(3.9\times {10}^{-5}\right)\left(3.02\times {10}^{-9}\right)}{4.8\times {10}^{-3}}=2.5\times {10}^{-11}M=\left[\text{Na}\left({\text{C}}_{7}{\text{H}}_{4}{\text{NSO}}_{3}\right)\right][/latex]
Glossary
buffer capacity: amount of an acid or base that can be added to a volume of a buffer solution before its pH changes significantly (usually by one pH unit)
buffer: mixture of a weak acid or a weak base and the salt of its conjugate; the pH of a buffer resists change when small amounts of acid or base are added
Henderson-Hasselbalch equation: equation used to calculate the pH of buffer solutions
Candela Citations
CC licensed content, Shared previously
- Chemistry 2e. Provided by: OpenStax. Located at: https://openstax.org/. License: CC BY: Attribution. License Terms: Access for free at https://openstax.org/books/chemistry-2e/pages/1-introduction

![A graph is shown with a horizontal axis labeled “Added m L of 0.10 M N a O H” which has markings and vertical gridlines every 10 units from 0 to 110. The vertical axis is labeled “p H” and is marked every 1 unit beginning at 0 extending to 11. A break is shown in the vertical axis between 0 and 4. A red curve is drawn on the graph which increases gradually from the point (0, 4.8) up to about (100, 7) after which the graph has a vertical section up to about (100, 11). The curve is labeled [ C H subscript 3 C O subscript 2 H ] is 11 percent of [ C H subscript 3 CO subscript 2 superscript negative].](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/219/2016/08/09044040/CNX_Chem_14_06_buffer.jpg)

![Eight tan rectangles are shown in four columns of two rectangles each that are connected with right pointing arrows. The first rectangle in the upper left is labeled “Volume of N a O H solution.” An arrow points right to a second rectangle labeled “Moles of N a O H added.” A second arrow points right to a third rectangle labeled “Additional moles of N a C H subscript 3 C O subscript 2.” Just beneath the first rectangle in the upper left is a rectangle labeled “Volume of buffer solution.” An arrow points right to another rectangle labeled “Initial moles of C H subscript 3 C O subscript 2 H.” This rectangle points to the same third rectangle, which is labeled “ Additional moles of N a C H subscript 3 C O subscript 2.” An arrow points right to a rectangle labeled “ Unreacted moles of C H subscript 3 C O subscript 2 H.” An arrow points from this rectangle to a rectangle below labeled “[ C H subscript 3 C O subscript 2 H ].” An arrow extends below the “Additional moles of N a C H subscript 3 C O subscript 2” rectangle to a rectangle labeled “[ C H subscript 3 C O subscript 2 ].” This rectangle points right to the rectangle labeled “[ C H subscript 3 C O subscript 2 H ].”](https://s3-us-west-2.amazonaws.com/courses-images/wp-content/uploads/sites/219/2016/08/09043740/CNX_Chem_14_06_steps2_img.jpg)
 This series of calculations gives a pH = 4.75. Thus the addition of the base barely changes the pH of the solution (F).
This series of calculations gives a pH = 4.75. Thus the addition of the base barely changes the pH of the solution (F).