Introduction
What you’ll learn to do: Utilize methods for visualizing data
The following video provides many examples of how contextualized, visually beautiful numbers add meaning and relevance to our life. Watch the first three minutes to get a flavor for data visualization.
In this section, we’ll explore how to make information meaningful in a visual format. We will present some of the most common ways data is represented graphically. We will also discuss some of the ways you can increase the accuracy and effectiveness of graphs of data that you create. Data visualization will help us solve some problems more quickly, and allow us better understanding for how to compare different types of information to make better decisions as a result.
Learning Outcomes
- Create a frequency table that represents a data set
- Create and analyze a bar graph that represents a data set
- Create a Pareto chart that represents a data set
- Create and analyze a pie chart that represents a data set
- Create and analyze a histogram that represents a data set
Visualizing Categorical Data
Categorical, or qualitative, data are pieces of information that allow us to classify the objects under investigation into various categories. We usually begin working with categorical data by summarizing the data into a frequency table.
Frequency Table
A frequency table is a table with two columns. One column lists the categories, and another for the frequencies with which the items in the categories occur (how many items fit into each category).
Example
An insurance company determines vehicle insurance premiums based on known risk factors. If a person is considered a higher risk, their premiums will be higher. One potential factor is the color of your car. The insurance company believes that people with some color cars are more likely to get in accidents. To research this, they examine police reports for recent total-loss collisions. The data are summarized in the frequency table below which describes the frequency of each car color involved in a total-loss collision.
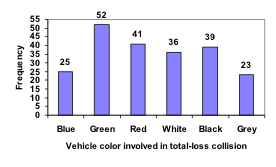
| Color | Frequency |
| Blue | 25 |
| Green | 52 |
| Red | 41 |
| White | 36 |
| Black | 39 |
| Grey | 23 |
Try It
Sometimes we need an even more intuitive way of displaying data. This is where charts and graphs come in. There are many, many ways of displaying data graphically, but we will concentrate on just a few, the first of which is called a bar graph. In this section, we will work with bar graphs that display categorical data; the next section will be devoted to a type of bar graph called a histogram that displays quantitative data.
Bar graph
A bar graph is a graph that displays a bar for each category with the length of each bar indicating the frequency of that category.
To construct a bar graph, we need to draw a vertical axis and a horizontal axis. The vertical direction will have a scale and measure the frequency of each category; the horizontal axis has no scale in this instance. The construction of a bar chart is most easily described by use of an example.
example
Using our car data from above, note the highest frequency is 52, so our vertical axis needs to go from 0 to 52, but we might as well use 0 to 55, so that we can put a hash mark every 5 units:
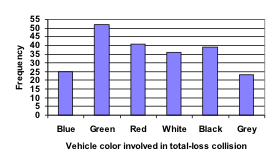
Notice that the height of each bar is determined by the frequency of the corresponding color. The horizontal gridlines are a nice touch, but not necessary. In practice, you will find it useful to draw bar graphs using graph paper, so the gridlines will already be in place, or using technology. Instead of gridlines, we might also list the frequencies at the top of each bar, like this:
The following video explains the process and value of moving data from a table to a bar graph.
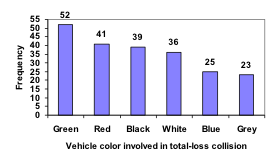
In the previous example, our chart might benefit from being reordered from largest to smallest frequency values. This arrangement can make it easier to compare similar values in the chart, even without gridlines. When we arrange the categories in decreasing frequency order like this, it is called a Pareto chart.
Pareto chart
A Pareto chart is a bar graph ordered from highest to lowest frequency
Example
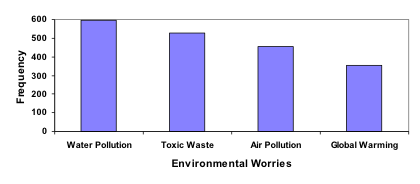
Transforming our bar graph from earlier into a Pareto chart, we get:
The following video addresses this example of building a Pareto chart.
Example
In a survey[1], adults were asked whether they personally worried about a variety of environmental concerns. The numbers (out of 1012 surveyed) who indicated that they worried “a great deal” about some selected concerns are summarized below. Construct a Pareto chart from the following frequency table.
| Environmental Issue | Frequency |
| Pollution of drinking water | 597 |
| Contamination of soil and water by toxic waste | 526 |
| Air pollution | 455 |
| Global warming | 354 |
To show relative sizes, it is common to use a pie chart.
Pie Chart
A pie chart is a circle with wedges cut of varying sizes marked out like slices of pie or pizza. The relative sizes of the wedges correspond to the relative frequencies of the categories.
Recall percents
In the pie chart examples that follow, you’ll need to be able to find percents from proportions as well as the percentage of a number.
Example 1: Find a percent given a part and a whole.
12 of 35 students are majoring in mass communications. Write this as a percent.
[latex]\dfrac{12}{35}\approx 0.343 = 34.3\%[/latex]
Example 2: Find the percentage of a whole.
What is 16% of 12,500? To find this number, you can translate the words into the equation: [latex]x=0.16\cdot12,500[/latex]; Find [latex]x[/latex].
Solving for [latex]x[/latex], we find that [latex]x = 2000[/latex].
example
Once again, let’s consider our vehicle color data.
| Color | Frequency |
| Blue | 25 |
| Green | 52 |
| Red | 41 |
| White | 36 |
| Black | 39 |
| Grey | 23 |
We would like to create a pie chart to visualize the relative frequencies of cars in the different color categories. To do this, we must first add up the total frequencies. This gives us 216 cars reported to be involved in total-loss collisions.
The relative frequency for each color is found by calculating the percentage of that color car involved in total-loss collision out of the number of all such cars. The relative frequencies are included in the table below.
| Color | Frequency | Relative Frequency |
| Blue | 25 | [latex]\frac{25}{216}=11.57\%[/latex] |
| Green | 52 | [latex]\frac{52}{216}=24.07\%[/latex] |
| Red | 41 | [latex]\frac{41}{216}=18.98\%[/latex] |
| White | 36 | [latex]\frac{36}{216}=16.67\%[/latex] |
| Black | 39 | [latex]\frac{39}{216}=18.06\%[/latex] |
| Grey | 23 | [latex]\frac{23}{216}=10.65\%[/latex] |
Using the relative frequencies, our pie chart might look like this:
This video demonstrates how to create pie charts like the one above.
Pie charts look nice, but are harder to draw by hand than bar charts since to draw them accurately we would need to compute the angle each wedge cuts out of the circle, then measure the angle with a protractor. Computers are much better suited to drawing pie charts. Common software programs like Microsoft Word or Excel, OpenOffice.org Write or Calc, or Google Sheets are able to create bar graphs, pie charts, and other graph types. There are also numerous online tools that can create graphs.[2]
Example
Create a bar graph and a pie chart to illustrate the grades on a history exam below.
A: 12 students, B: 19 students, C: 14 students, D: 4 students, F: 5 students
Example
In this example, we consider how to read a pie chart. The pie chart below shows the percentage of voters supporting each of three candidates running for a local senate seat. If there are 20,000 voters in the district, approximately how many support Reeves?
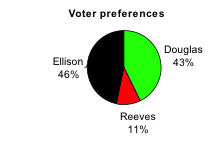
The following video works through this example.
Try It
Another way to visualize data is by creating a pictogram to illustrate either the frequencies or sizes of quantities being measured.
Pictogram
A pictogram is a statistical graphic in which the size of the picture is intended to represent the frequencies or sizes of the values being represented.
Exercises
College students surveyed at Mountain Range University averaged 8.5 hours a day on technology: 5.5 hours of these hours were spent playing video games or on social media and 3 hours, on average, doing school work. The survey results can be represented by the following pictogram.
Caution! When Visualizations are Misleading
While the intention behind creating visualizations for data is typically to make it quicker and easier to absorb information, it is also possible to create visuals that distort and misrepresent the data. In the next examples, we consider several potentially misleading visuals.
examples
Example 1: In this first example, the bar graph shown is a 3-dimensional attempt at something fancy and the distortion is likely unintentional. Sometimes people will add features to graphs that don’t help to convey their information. Three-dimensional graphs like this one are usually not as effective as their two-dimensional counterparts.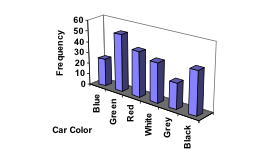
Example 2: A labor union might produce the graph below to illustrate the difference between the average manager salary and the average worker salary.
Looking at the picture, it would be reasonable to guess that the manager salaries is 4 times as large as the worker salaries – the area of the bag looks about 4 times as large. However, the manager salaries are in fact only twice as large as worker salaries, which were reflected in the picture by making the manager bag twice as tall.
The following video reviews the two examples of ineffective data representation in more detail.
Another distortion that can occur in bar charts results from setting the baseline to a value other than zero. The baseline is the bottom of the vertical axis, representing the least number of cases that could have occurred in a category. Normally, this number should be zero.
example
Compare the two graphs below showing support for same-sex marriage rights from a poll taken in December 2008[3]. Recall that relative frequency can be defined as the number of times an event occurs divided by the total number of events occurring in a given scenario or in this case (i.e.: the percent of occurrences).
The difference in the vertical scale on the first graph suggests a different story than the true differences in percentages, making it appear as if, in 2008, three times as many people opposed same-sex marriage rights as supported it.
In this graph, the vertical axis is skewed (starting at 40 instead of at 0).
Here, the vertical axis starts at 0 and gives a more accurate representation of the relative frequencies.
- Gallup Poll. March 5-8, 2009. http://www.pollingreport.com/enviro.htm ↵
- For example: http://nces.ed.gov/nceskids/createAgraph/ or http://docs.google.com ↵
- CNN/Opinion Research Corporation Poll. Dec 19-21, 2008, from http://www.pollingreport.com/civil.htm ↵
