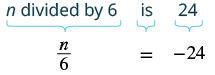Translating Words to Equations and Solving

Learning Outcomes

Translate statements into equations and solve

Translate Sentences to Equations and Solve

Recall the four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference. We will use these to solve equations that contain fractions.

Subtraction Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex]

if [latex]a=b[/latex], then [latex]a-c=b-c[/latex].

Addition Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex]

if [latex]a=b[/latex], then [latex]a+c=b+c[/latex].

Division Property of Equality:

For any numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c,}}[/latex] where [latex]\mathit{\text{c}}\ne \mathit{0}[/latex]

if [latex]a=b[/latex], then [latex] \Large\frac{a}{c}= \Large\frac{b}{c}[/latex]

Multiplication Property of Equality:

For any real numbers [latex]\mathit{\text{a, b,}}[/latex] and [latex]\mathit{\text{c}}[/latex]

if [latex]a=b[/latex], then [latex]ac=bc[/latex]

When you add, subtract, multiply or divide the same quantity from both sides of an equation, you still have equality.

In the next few examples, we’ll translate sentences that contain fractions into equations and then solve the equations. When we translate sentences into equations, we start by locating the “equals” word or words and translating them into an equals sign. (Note: This could be the phrase “is equal to” or simply the word “is”). We then translate the words to the left of the “equals” word(s) into an algebraic expression and the words to the right of the “equals” word(s) into an algebraic expression.

In the next examples we will use the Multiplication Property of Equality to solve the equation.

Example

Translate and solve: [latex]n[/latex] divided by [latex]6[/latex] is [latex]-24[/latex].

Solution:

Translate.
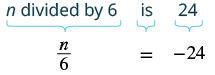Multiply both sides by [latex]6[/latex] .		[latex]\color{red}{6}\cdot\Large\frac{n}{6}\normalsize=\color{red}{6}(-24)[/latex]
Simplify.		[latex]n=-144[/latex]
Check:	Is [latex]-144[/latex] divided by [latex]6[/latex] equal to [latex]-24[/latex] ?
Translate.	[latex]\Large\frac{-144}{6}\normalsize\stackrel{?}{=}-24[/latex]
Simplify. It checks.	[latex]-24=-24\quad\checkmark[/latex]

Translate.
Multiply both sides by [latex]-5[/latex] .		[latex]\color{red}{5}\Large(\frac{q}{-5}) \normalsize= \color{red}{-5}(70)[/latex]
Simplify.		[latex]q=-350[/latex]
Check:	Is the quotient of [latex]-350[/latex] and [latex]-5[/latex] equal to [latex]70[/latex] ?
Translate.	[latex]\Large\frac{-350}{-5}\normalsize\stackrel{?}{=}70[/latex]
Simplify. It checks.	[latex]70=70\quad\checkmark[/latex]

Translate.
Multiply both sides by [latex]\Large\frac{3}{2}[/latex] .		[latex]\color{red}{\Large\frac{3}{2}}\cdot\Large\frac{2}{3}\normalsize f=\color{red}{\Large\frac{3}{2}}\cdot \normalsize18[/latex]
Simplify.		[latex]f=27[/latex]
Check:	Is two-thirds of [latex]27[/latex] equal to [latex]18[/latex] ?
Translate.	[latex]\Large\frac{2}{3}\normalsize(27)\normalsize\stackrel{?}{=}18[/latex]
Simplify. It checks.	[latex]18=18\quad\checkmark[/latex]

		The quotient of [latex]m[/latex] and [latex]\Large\frac{5}{6}[/latex] is [latex]\Large\frac{3}{4}[/latex] .
Translate.		[latex]\Large\frac{m}{\LARGE\frac{5}{6}}=\Large\frac{3}{4}[/latex]
Multiply both sides by [latex]\Large\frac{5}{6}[/latex] to isolate [latex]m[/latex] .		[latex]\Large\frac{5}{6}\left(\Large\frac{m}{\LARGE\frac{5}{6}}\right)=\Large\frac{5}{6}\left(\Large\frac{3}{4}\right)[/latex]
Simplify.		[latex]m=\Large\frac{5\cdot 3}{6\cdot 4}[/latex]
Remove common factors and multiply.		[latex]m=\Large\frac{5}{8}[/latex]
Check:
Is the quotient of [latex]\Large\frac{5}{8}[/latex] and [latex]\Large\frac{5}{6}[/latex] equal to [latex]\Large\frac{3}{4}[/latex] ?	[latex]\Large\frac{\LARGE\frac{5}{8}}{\LARGE\frac{5}{6}}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Rewrite as division.	[latex]\Large\frac{5}{8}\div\Large\frac{5}{6}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Multiply the first fraction by the reciprocal of the second.	[latex]\Large\frac{5}{8}\cdot\Large\frac{6}{5}\stackrel{?}{=}\Large\frac{3}{4}[/latex]
Simplify.	[latex]\Large\frac{3}{4}=\Large\frac{3}{4}\quad\checkmark[/latex]

Translate.
Use the Subtraction Property of Equality to subtract [latex]\Large\frac{3}{8}[/latex] from both sides.	[latex]\Large\frac{3}{8}+\normalsize x-\Large\frac{3}{8}=\normalsize3\Large\frac{1}{2}-\Large\frac{3}{8}[/latex]
Combine like terms on the left side.	[latex]x=3\Large\frac{1}{2}-\Large\frac{3}{8}[/latex]
Convert mixed number to improper fraction.	[latex]x=\Large\frac{7}{2}-\Large\frac{3}{8}[/latex]
Convert to equivalent fractions with LCD of [latex]8[/latex].	[latex]x=\Large\frac{28}{8}-\Large\frac{3}{8}[/latex]
Subtract.	[latex]x=\Large\frac{25}{8}[/latex]
Write as a mixed number.	[latex]x=3\Large\frac{1}{8}[/latex]

	[latex]\Large\frac{3}{8}\normalsize+3\Large\frac{1}{8}\normalsize\stackrel{?}{=}3\Large\frac{1}{2}[/latex]
Add.	[latex]3\Large\frac{4}{8}\normalsize\stackrel{?}{=}3\Large\frac{1}{2}[/latex]
Simplify.	[latex]3\Large\frac{1}{2}\normalsize=3\Large\frac{1}{2}\quad\checkmark[/latex]

UNIT 4