Section 3.1 Solutions

1. Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.

3. An asymptote is a line that the graph of a function approaches, as x either increases or decreases without bound. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.

5. exponential; the population decreases by a proportional rate.

7. not exponential; the charge decreases by a constant amount each visit, so the statement represents a linear function.

9. The forest represented by the function $B\left(t\right)=82{\left(1.029\right)}^{t}$.

11. After t = 20 years, forest A will have 43 more trees than forest B.

13. Answers will vary. Sample response: For a number of years, the population of forest A will increasingly exceed forest B, but because forest B actually grows at a faster rate, the population will eventually become larger than forest A and will remain that way as long as the population growth models hold. Some factors that might influence the long-term validity of the exponential growth model are drought, an epidemic that culls the population, and other environmental and biological factors.

15. exponential growth; The growth factor, 1.06, is greater than 1.

17. exponential decay; The decay factor, 0.97, is between 0 and 1.

19. $f\left(x\right)=2000{\left(0.1\right)}^{x}$

21. $f\left(x\right)={\left(\frac{1}{6}\right)}^{-\frac{3}{5}}{\left(\frac{1}{6}\right)}^{\frac{x}{5}}\approx 2.93{\left(0.699\right)}^{x}$

23. $10,250

25. $13,268.58

27. $P=A\left(t\right)\cdot {\left(1+\frac{r}{n}\right)}^{-nt}$

29. $4,572.56

31. 4%

33. continuous growth; the growth rate is greater than 0.

35. $104,053.65

37. 6.9% compounded continuously

39. $g\left(x\right)=4{\left(3\right)}^{-x}$; y-intercept: $\left(0,4\right)$; Domain: all real numbers; Range: all real numbers greater than 0.

41. $g\left(x\right)=-{10}^{x}+7$; y-intercept: $\left(0,6\right)$; Domain: all real numbers; Range: all real numbers less than 7.

43. $g\left(x\right)=2{\left(\frac{1}{4}\right)}^{x}$; y-intercept: $\left(0,\text{ 2}\right)$; Domain: all real numbers; Range: all real numbers greater than 0.

45. y-intercept: $\left(0,-2\right)$

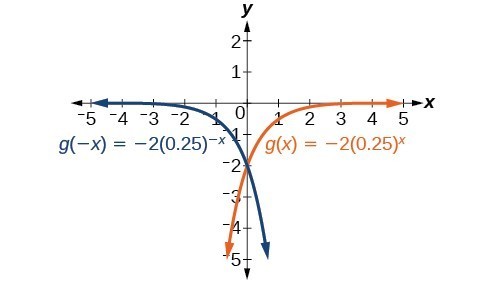
47.

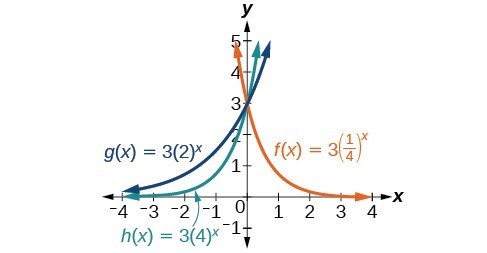
49. B

51. A

53. E

55. D

57. C

59.

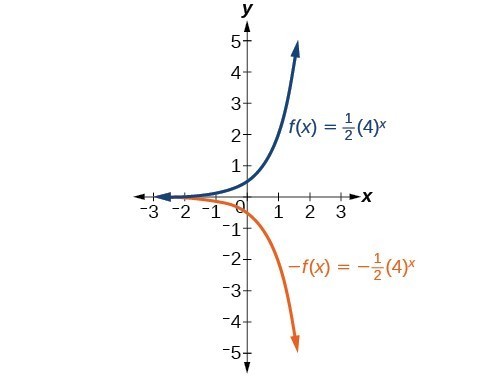
61.

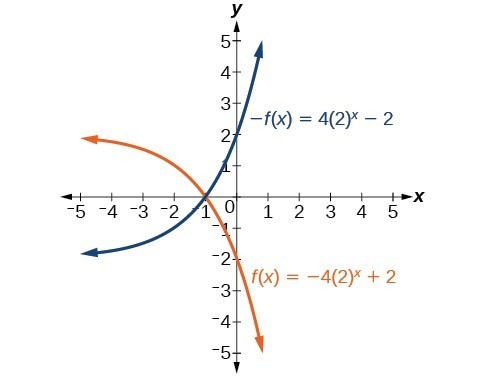
63. Horizontal asymptote: $h\left(x\right)=3$; Domain: all real numbers; Range: all real numbers strictly greater than 3.

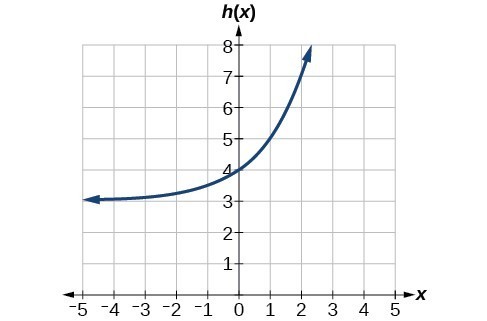
65. As $x\to \infty\text{ , }f\left(x\right)\to -\infty$;
As $x\to -\infty\text{ , }f\left(x\right)\to -1$

67. As $x\to \infty\text{ , }f\left(x\right)\to 2$;
As $x\to -\infty\text{ , }f\left(x\right)\to \infty$

69. $f\left(x\right)={4}^{x}-3$

71. $f\left(x\right)={4}^{x - 5}$

73. $f\left(x\right)={4}^{-x}$

75. $y=-{2}^{x}+3$

77. $y=-2{\left(3\right)}^{x}+7$

79. $g\left(6\right)=800+\frac{1}{3}\approx 800.3333$

81. $h\left(-7\right)=-58$

83. $x\approx -2.953$

85. $x\approx -0.222$

87. Let f be the exponential decay function $f\left(x\right)=a\cdot {\left(\frac{1}{b}\right)}^{x}$ such that $b>1$. Then for some number $n>0$, $f\left(x\right)=a\cdot {\left(\frac{1}{b}\right)}^{x}=a{\left({b}^{-1}\right)}^{x}=a{\left({\left({e}^{n}\right)}^{-1}\right)}^{x}=a{\left({e}^{-n}\right)}^{x}=a{\left(e\right)}^{-nx}$.

89. 47,622 foxes

91. $82,247.78; $449.75

93. The graph of $G\left(x\right)={\left(\frac{1}{b}\right)}^{x}$ is the reflection about the y-axis of the graph of $F\left(x\right)={b}^{x}$; For any real number $b>0$ and function $f\left(x\right)={b}^{x}$, the graph of ${\left(\frac{1}{b}\right)}^{x}$ is the the reflection about the y-axis, $F\left(-x\right)$.

95. The graphs of $g\left(x\right)$ and $h\left(x\right)$ are the same and are a horizontal shift to the right of the graph of $f\left(x\right)$; For any real number n, real number $b>0$, and function $f\left(x\right)={b}^{x}$, the graph of $\left(\frac{1}{{b}^{n}}\right){b}^{x}$ is the horizontal shift $f\left(x-n\right)$.

Section 3.2 Solutions

1. A logarithm is an exponent. Specifically, it is the exponent to which a base b is raised to produce a given value. In the expressions given, the base b has the same value. The exponent, y, in the expression ${b}^{y}$ can also be written as the logarithm, ${\mathrm{log}}_{b}x$, and the value of x is the result of raising b to the power of y.

3. Since the equation of a logarithm is equivalent to an exponential equation, the logarithm can be converted to the exponential equation ${b}^{y}=x$\\, and then properties of exponents can be applied to solve for x.

5. The natural logarithm is a special case of the logarithm with base b in that the natural log always has base e. Rather than notating the natural logarithm as ${\mathrm{log}}_{e}\left(x\right)$, the notation used is $\mathrm{ln}\left(x\right)$.

7. Since the functions are inverses, their graphs are mirror images about the line y = x. So for every point $\left(a,b\right)$ on the graph of a logarithmic function, there is a corresponding point $\left(b,a\right)$ on the graph of its inverse exponential function.

9. No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.

11. ${a}^{c}=b$

13. ${x}^{y}=64$

15. ${15}^{b}=a$

17. ${13}^{a}=142$

19. ${e}^{n}=w$

21. ${\text{log}}_{c}\left(k\right)=d$

23. ${\mathrm{log}}_{19}y=x$

25. ${\mathrm{log}}_{n}\left(103\right)=4$

27. ${\mathrm{log}}_{y}\left(\frac{39}{100}\right)=x$

29. $\text{ln}\left(h\right)=k$

31. $x={2}^{-3}=\frac{1}{8}$

33. $x={3}^{3}=27$

35. $x={9}^{\frac{1}{2}}=3$

37. $x={6}^{-3}=\frac{1}{216}$

39. $x={e}^{2}$

41. 32

43. 1.06

45. 14.125

47. $\frac{1}{2}$

49. 4

51. –3

53. –12

55. 0

57. 10

59. 2.708

61. 0.151

63. Domain: $\left(-\infty ,\frac{1}{2}\right)$; Range: $\left(-\infty ,\infty \right)$

65. Domain: $\left(-\frac{17}{4},\infty \right)$; Range: $\left(-\infty ,\infty \right)$

67. Domain: $\left(5,\infty \right)$; Vertical asymptote: x = 5

69. Domain: $\left(-\frac{1}{3},\infty \right)$; Vertical asymptote: $x=-\frac{1}{3}$

71. Domain: $\left(-3,\infty \right)$; Vertical asymptote: x = –3

73. Domain: $\left(\frac{3}{7},\infty \right)$; Vertical asymptote: $x=\frac{3}{7}$ ; End behavior: as $x\to {\left(\frac{3}{7}\right)}^{+},f\left(x\right)\to -\infty$ and as $x\to \infty ,f\left(x\right)\to \infty$

75. Domain: $\left(-3,\infty \right)$ ; Vertical asymptote: x = –3; End behavior: as $x\to -{3}^{+}$ , $f\left(x\right)\to -\infty$ and as $x\to \infty$ , $f\left(x\right)\to \infty$

77. Domain: $\left(1,\infty \right)$; Range: $\left(-\infty ,\infty \right)$; Vertical asymptote: x = 1; x-intercept: $\left(\frac{5}{4},0\right)$; y-intercept: DNE

79. Domain: $\left(-\infty ,0\right)$; Range: $\left(-\infty ,\infty \right)$; Vertical asymptote: x = 0; x-intercept: $\left(-{e}^{2},0\right)$; y-intercept: DNE

81. Domain: $\left(0,\infty \right)$; Range: $\left(-\infty ,\infty \right)$; Vertical asymptote: x = 0; x-intercept: $\left({e}^{3},0\right)$; y-intercept: DNE

83. B

85. C

87. B

89. C

91.

93.

95. C

97.

99.

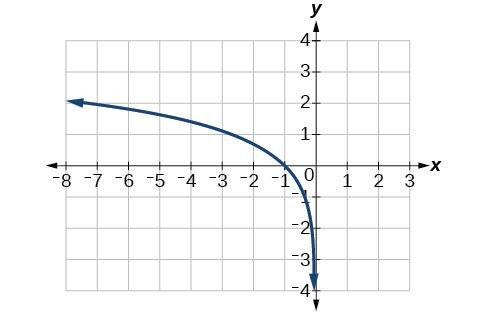
101.

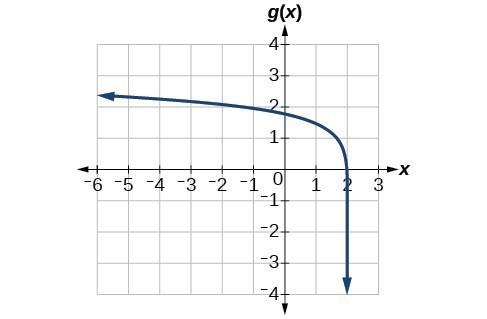
103. $f\left(x\right)={\mathrm{log}}_{2}\left(-\left(x - 1\right)\right)$

105. $f\left(x\right)=3{\mathrm{log}}_{4}\left(x+2\right)$

107. The graphs of $f\left(x\right)={\mathrm{log}}_{\frac{1}{2}}\left(x\right)$ and $g\left(x\right)=-{\mathrm{log}}_{2}\left(x\right)$ appear to be the same; Conjecture: for any positive base $b\ne 1$, ${\mathrm{log}}_{b}\left(x\right)=-{\mathrm{log}}_{\frac{1}{b}}\left(x\right)$.

109. Recall that the argument of a logarithmic function must be positive, so we determine where $\frac{x+2}{x - 4}>0$ . From the graph of the function $f\left(x\right)=\frac{x+2}{x - 4}$, note that the graph lies above the x-axis on the interval $\left(-\infty ,-2\right)$ and again to the right of the vertical asymptote, that is $\left(4,\infty \right)$. Therefore, the domain is $\left(-\infty ,-2\right)\cup \left(4,\infty \right)$.

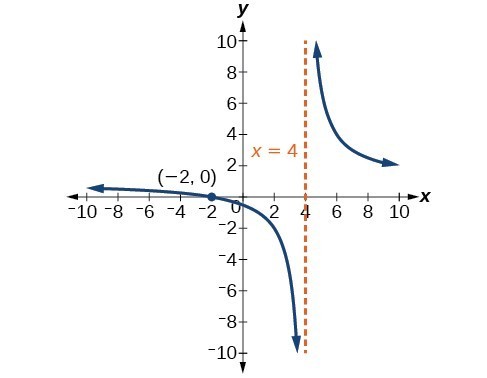
111. No, the function has no defined value for x = 0. To verify, suppose x = 0 is in the domain of the function $f\left(x\right)=\mathrm{log}\left(x\right)$. Then there is some number n such that $n=\mathrm{log}\left(0\right)$. Rewriting as an exponential equation gives: ${10}^{n}=0$, which is impossible since no such real number n exists. Therefore, x = 0 is not the domain of the function $f\left(x\right)=\mathrm{log}\left(x\right)$.

113. Yes. Suppose there exists a real number x such that $\mathrm{ln}x=2$. Rewriting as an exponential equation gives $x={e}^{2}$, which is a real number. To verify, let $x={e}^{2}$. Then, by definition, $\mathrm{ln}\left(x\right)=\mathrm{ln}\left({e}^{2}\right)=2$.

115. No; $\mathrm{ln}\left(1\right)=0$, so $\frac{\mathrm{ln}\left({e}^{1.725}\right)}{\mathrm{ln}\left(1\right)}$ is undefined.

117. 2

Section 3.3 Solutions

1. Any root expression can be rewritten as an expression with a rational exponent so that the power rule can be applied, making the logarithm easier to calculate. Thus, ${\mathrm{log}}_{b}\left({x}^{\frac{1}{n}}\right)=\frac{1}{n}{\mathrm{log}}_{b}\left(x\right)$.

3. ${\mathrm{log}}_{b}\left(2\right)+{\mathrm{log}}_{b}\left(7\right)+{\mathrm{log}}_{b}\left(x\right)+{\mathrm{log}}_{b}\left(y\right)$

5. ${\mathrm{log}}_{b}\left(13\right)-{\mathrm{log}}_{b}\left(17\right)$

7. $-k\mathrm{ln}\left(4\right)$

9. $\mathrm{ln}\left(7xy\right)$

11. ${\mathrm{log}}_{b}\left(4\right)$

13. ${\text{log}}_{b}\left(7\right)$

15. $15\mathrm{log}\left(x\right)+13\mathrm{log}\left(y\right)-19\mathrm{log}\left(z\right)$

17. $\frac{3}{2}\mathrm{log}\left(x\right)-2\mathrm{log}\left(y\right)$

19. $\frac{8}{3}\mathrm{log}\left(x\right)+\frac{14}{3}\mathrm{log}\left(y\right)$

21. $\mathrm{ln}\left(2{x}^{7}\right)$

23. $\mathrm{log}\left(\frac{x{z}^{3}}{\sqrt{y}}\right)$

25. ${\mathrm{log}}_{7}\left(15\right)=\frac{\mathrm{ln}\left(15\right)}{\mathrm{ln}\left(7\right)}$

27. ${\mathrm{log}}_{11}\left(5\right)=\frac{{\mathrm{log}}_{5}\left(5\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{1}{b}$

29. ${\mathrm{log}}_{11}\left(\frac{6}{11}\right)=\frac{{\mathrm{log}}_{5}\left(\frac{6}{11}\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{{\mathrm{log}}_{5}\left(6\right)-{\mathrm{log}}_{5}\left(11\right)}{{\mathrm{log}}_{5}\left(11\right)}=\frac{a-b}{b}=\frac{a}{b}-1$

31. 3

33. 2.81359

35. 0.93913

37. –2.23266

39. x = 4; By the quotient rule: ${\mathrm{log}}_{6}\left(x+2\right)-{\mathrm{log}}_{6}\left(x - 3\right)={\mathrm{log}}_{6}\left(\frac{x+2}{x - 3}\right)=1$.

Rewriting as an exponential equation and solving for x:

$\begin{cases}{6}^{1}\hfill & =\frac{x+2}{x - 3}\hfill \\ 0\hfill & =\frac{x+2}{x - 3}-6\hfill \\ 0\hfill & =\frac{x+2}{x - 3}-\frac{6\left(x - 3\right)}{\left(x - 3\right)}\hfill \\ 0\hfill & =\frac{x+2 - 6x+18}{x - 3}\hfill \\ 0\hfill & =\frac{x - 4}{x - 3}\hfill \\ \text{ }x\hfill & =4\hfill \end{cases}$

Checking, we find that ${\mathrm{log}}_{6}\left(4+2\right)-{\mathrm{log}}_{6}\left(4 - 3\right)={\mathrm{log}}_{6}\left(6\right)-{\mathrm{log}}_{6}\left(1\right)$ is defined, so x = 4.

41. Let b and n be positive integers greater than 1. Then, by the change-of-base formula, ${\mathrm{log}}_{b}\left(n\right)=\frac{{\mathrm{log}}_{n}\left(n\right)}{{\mathrm{log}}_{n}\left(b\right)}=\frac{1}{{\mathrm{log}}_{n}\left(b\right)}$.

Section 3.4 Solutions

1. Determine first if the equation can be rewritten so that each side uses the same base. If so, the exponents can be set equal to each other. If the equation cannot be rewritten so that each side uses the same base, then apply the logarithm to each side and use properties of logarithms to solve.

3. The one-to-one property can be used if both sides of the equation can be rewritten as a single logarithm with the same base. If so, the arguments can be set equal to each other, and the resulting equation can be solved algebraically. The one-to-one property cannot be used when each side of the equation cannot be rewritten as a single logarithm with the same base.

5. $x=-\frac{1}{3}$

7. n = –1

9. $b=\frac{6}{5}$

11. x = 10

13. No solution

15. $p=\mathrm{log}\left(\frac{17}{8}\right)-7$

17. $k=-\frac{\mathrm{ln}\left(38\right)}{3}$

19. $x=\frac{\mathrm{ln}\left(\frac{38}{3}\right)-8}{9}$

21. $x=\mathrm{ln}12$

23. $x=\frac{\mathrm{ln}\left(\frac{3}{5}\right)-3}{8}$

25. no solution

27. $x=\mathrm{ln}\left(3\right)$

29. ${10}^{-2}=\frac{1}{100}$

31. n = 49

33. $k=\frac{1}{36}$

35. $x=\frac{9-e}{8}$

37. x = 2

39. x = -3

41. x = 4

43. x = $\frac{11}{2}$

45. x = 12

47. n = 1

49. No solution

51. No solution

53. $x=\pm \frac{10}{3}$

55. x = 10

57. x = 0

59. $x=\frac{3}{4}$

61. x = 9

63. $x=\frac{{e}^{2}}{3}\approx 2.5$

65. x = –5

67. $x=\frac{e+10}{4}\approx 3.2$

69. No solution

71. $x=\frac{11}{5}\approx 2.2$

73. $x=\frac{101}{11}\approx 9.2$

75. about $27,710.24

77. about 5 years

79. $\frac{\mathrm{ln}\left(17\right)}{5}\approx 0.567$

81. $x=\frac{\mathrm{log}\left(38\right)+5\mathrm{log}\left(3\right)\text{ }}{4\mathrm{log}\left(3\right)}\approx 2.078$

83. $x\approx 2.2401$

85. $x\approx -44655.7143$

87. about 5.83

89. $t=\mathrm{ln}\left({\left(\frac{y}{A}\right)}^{\frac{1}{k}}\right)$

91. $t=\mathrm{ln}\left({\left(\frac{T-{T}_{s}}{{T}_{0}-{T}_{s}}\right)}^{-\frac{1}{k}}\right)$

Section 3.5 Solutions

1. Half-life is a measure of decay and is thus associated with exponential decay models. The half-life of a substance or quantity is the amount of time it takes for half of the initial amount of that substance or quantity to decay.

3. Doubling time is a measure of growth and is thus associated with exponential growth models. The doubling time of a substance or quantity is the amount of time it takes for the initial amount of that substance or quantity to double in size.

5. a) $A=1000{e}^{0.5879x}$ b) approximately 10498 flies c) About 5.8 days

7. $f\left(0\right)\approx 16.7$; The amount initially present is about 16.7 units.

9. 150

11. exponential; $f\left(x\right)={1.2}^{x}$

13.

15. about 1.4 years

17. about 7.3 years

19. 4 half-lives; 8.18 minutes

21. $\begin{cases}\text{ }M=\frac{2}{3}\mathrm{log}\left(\frac{S}{{S}_{0}}\right)\hfill \\ \mathrm{log}\left(\frac{S}{{S}_{0}}\right)=\frac{3}{2}M\hfill \\ \text{ }\frac{S}{{S}_{0}}={10}^{\frac{3M}{2}}\hfill \\ \text{ }S={S}_{0}{10}^{\frac{3M}{2}}\hfill \end{cases}$

23. Let $y={b}^{x}$ for some non-negative real number b such that $b\ne 1$. Then,
$\begin{cases}\mathrm{ln}\left(y\right)=\mathrm{ln}\left({b}^{x}\right)\hfill \\ \mathrm{ln}\left(y\right)=x\mathrm{ln}\left(b\right)\hfill \\ {e}^{\mathrm{ln}\left(y\right)}={e}^{x\mathrm{ln}\left(b\right)}\hfill \\ y={e}^{x\mathrm{ln}\left(b\right)}\hfill \end{cases}$

25. $A=125{e}^{\left(-0.3567t\right)};A\approx 43$ mg

27. about 60 days

29. $f\left(t\right)=250{e}^{\left(-0.00914t\right)}$; half-life: about $\text{76}$ minutes

31. $r\approx -0.0667$, So the hourly decay rate is about 6.67%

33. $f\left(t\right)=1350{e}^{\left(0.03466t\right)}$; after 3 hours: $P\left(180\right)\approx 691,200$

35. $f\left(t\right)=256{e}^{\left(0.068110t\right)}$; doubling time: about 10 minutes

37. MMS magnitude: 5.82

39. $N\left(3\right)\approx 71$

41. C