Section 5.3: Double Angle, Half Angle, and Reduction Formulas

Learning Outcomes

Use double-angle formulas to find exact values.
Use double-angle formulas to verify identities.
Use reduction formulas to simplify an expression.
Use half-angle formulas to find exact values.

Using Double-Angle Formulas to Find Exact Values

In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where $\alpha =\beta$ . Deriving the double-angle formula for sine begins with the sum formula,

sin (α + β) = sin α cos β + cos α sin β

$\sin \left(\alpha +\beta \right)=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

If we let $\alpha =\beta =\theta$ , then we have

\begin{matrix} sin (θ + θ) & = sin θ cos θ + cos θ sin θ sin (2 θ) & = 2 sin θ cos θ \end{matrix}

$\begin{align}\sin \left(\theta +\theta \right)&=\sin \theta \cos \theta +\cos \theta \sin \theta \\ \sin \left(2\theta \right)&=2\sin \theta \cos \theta \end{align}$

Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, $\cos \left(\alpha +\beta \right)=\cos \alpha \cos \beta -\sin \alpha \sin \beta$ , and letting $\alpha =\beta =\theta$ , we have

\begin{matrix} cos (θ + θ) & = cos θ cos θ - sin θ sin θ cos (2 θ) & = {cos}^{2} θ - {sin}^{2} θ \end{matrix}

$\begin{align}\cos \left(\theta +\theta \right)&=\cos \theta \cos \theta -\sin \theta \sin \theta \\ \cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \end{align}$

Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more interpretations. The first one is:

\begin{matrix} cos (2 θ) & = {cos}^{2} θ - {sin}^{2} θ = (1 - {sin}^{2} θ) - {sin}^{2} θ = 1 - 2 {sin}^{2} θ \end{matrix}

$\begin{align}\cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &=\left(1-{\sin }^{2}\theta \right)-{\sin }^{2}\theta \\ &=1 - 2{\sin }^{2}\theta\end{align}$

The second interpretation is:

\begin{matrix} cos (2 θ) & = {cos}^{2} θ - {sin}^{2} θ = {cos}^{2} θ - (1 - {cos}^{2} θ) = 2 {cos}^{2} θ - 1 \end{matrix}

$\begin{align}\cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &={\cos }^{2}\theta -\left(1-{\cos }^{2}\theta \right) \\ &=2{\cos }^{2}\theta -1\end{align}$

Similarly, to derive the double-angle formula for tangent, replacing $\alpha =\beta =\theta$ in the sum formula gives

\begin{matrix} tan (α + β) & = \frac{tan α + tan β}{1 - tan α tan β} tan (θ + θ) & = \frac{tan θ + tan θ}{1 - tan θ tan θ} tan (2 θ) & = \frac{2 tan θ}{1 - {tan}^{2} θ} \end{matrix}

$\begin{align}\tan \left(\alpha +\beta \right)&=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }\\ \tan \left(\theta +\theta \right)&=\frac{\tan \theta +\tan \theta }{1-\tan \theta \tan \theta }\\ \tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }\end{align}$

A General Note: Double-Angle Formulas

The double-angle formulas are summarized as follows:

$\begin{align}\sin \left(2\theta \right)&=2\sin \theta \cos \theta\\\text{ }\\ \cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &=1 - 2{\sin }^{2}\theta \\ &=2{\cos }^{2}\theta -1 \\\text{ }\\ \tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }\end{align}$

How To: Given the tangent of an angle and the quadrant in which it is located, use the double-angle formulas to find the exact value.

Draw a triangle to reflect the given information.
Determine the correct double-angle formula.
Substitute values into the formula based on the triangle.
Simplify.

Example 1: Using a Double-Angle Formula to Find the Exact Value Involving Tangent

Given that $\tan \theta =−\frac{3}{4}$ and $\theta$ is in quadrant II, find the following:

$\sin \left(2\theta \right)$
$\cos \left(2\theta \right)$
$\tan \left(2\theta \right)$

Show Solution

If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given $\tan \theta =-\frac{3}{4}$ , such that $\theta$ is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because $\theta$ is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:

$\begin{align}{\left(-4\right)}^{2}+{\left(3\right)}^{2}&={c}^{2}\\ 16+9&={c}^{2}\\ 25&={c}^{2}\\ c&=5\end{align}$

Now we can draw a triangle similar to the one shown in Figure 2.

Diagram of a triangle in the x,y-plane. The vertices are at the origin, (-4,0), and (-4,3). The angle at the origin is theta. The angle formed by the side (-4,3) to (-4,0) forms a right angle with the x axis. The hypotenuse across from the right angle is length 5.

Figure 2

Let’s begin by writing the double-angle formula for sine.
$\sin \left(2\theta \right)=2\sin \theta \cos \theta$

We see that we to need to find $\sin \theta$ and $\cos \theta$ . Based on Figure 2, we see that the hypotenuse equals 5, so $\sin \theta =\frac{3}{5}$ , and $\cos \theta =−\frac{4}{5}$ . Substitute these values into the equation, and simplify.
Thus,

$\begin{align}\sin \left(2\theta \right)&=2\left(\frac{3}{5}\right)\left(−\frac{4}{5}\right) \\ &=−\frac{24}{25} \end{align}$
Write the double-angle formula for cosine.
$\cos \left(2\theta \right)={\cos }^{2}\theta -{\sin }^{2}\theta$

Again, substitute the values of the sine and cosine into the equation, and simplify.

$\begin{align}\cos \left(2\theta \right)&={\left(−\frac{4}{5}\right)}^{2}−{\left(\frac{3}{5}\right)}^{2} \\ &=\frac{16}{25}−\frac{9}{25} \\ &=\frac{7}{25}\end{align}$
Write the double-angle formula for tangent.
$\tan \left(2\theta \right)=\frac{2\tan \theta }{1−{\tan }^{2}\theta }$

In this formula, we need the tangent, which we were given as $\tan \theta =−\frac{3}{4}$ . Substitute this value into the equation, and simplify.

$\begin{align}\tan \left(2\theta \right)&=\frac{2\left(-\frac{3}{4}\right)}{1-{\left(-\frac{3}{4}\right)}^{2}} \\ &=\frac{-\frac{3}{2}}{1-\frac{9}{16}} \\ &=-\frac{3}{2}\left(\frac{16}{7}\right) \\ &=-\frac{24}{7} \end{align}$

Try It

Given $\sin \alpha =\frac{5}{8}$ , with $\theta$ in quadrant I, find $\cos \left(2\alpha \right)$ .

Show Solution

$\cos \left(2\alpha \right)=\frac{7}{32}$

Try It

Example 2: Using the Double-Angle Formula for Cosine without Exact Values

Use the double-angle formula for cosine to write $\cos \left(6x\right)$ in terms of $\cos \left(3x\right)$ .

Show Solution

$\begin{align}\cos \left(6x\right)&=\cos \left(3x+3x\right) \\ &=\cos 3x\cos 3x-\sin 3x\sin 3x \\ &={\cos }^{2}3x-{\sin }^{2}3x \end{align}$

Analysis of the Solution

This example illustrates that we can use the double-angle formula without having exact values. It emphasizes that the pattern is what we need to remember and that identities are true for all values in the domain of the trigonometric function.

Using Double-Angle Formulas to Verify Identities

Establishing identities using the double-angle formulas is performed using the same steps we used to derive the sum and difference formulas. Choose the more complicated side of the equation and rewrite it until it matches the other side.

Example 3: Using the Double-Angle Formulas to Establish an Identity

Establish the following identity using double-angle formulas:

$1+\sin \left(2\theta \right)={\left(\sin \theta +\cos \theta \right)}^{2}$

Show Solution

We will work on the right side of the equal sign and rewrite the expression until it matches the left side.

$\begin{align}{\left(\sin \theta +\cos \theta \right)}^{2}&={\sin }^{2}\theta +2\sin \theta \cos \theta +{\cos }^{2}\theta \\ &=\left({\sin }^{2}\theta +{\cos }^{2}\theta \right)+2\sin \theta \cos \theta \\ &=1+2\sin \theta \cos \theta \\ &=1+\sin \left(2\theta \right)\end{align}$

Analysis of the Solution

This process is not complicated, as long as we recall the perfect square formula from algebra:

${\left(a\pm b\right)}^{2}={a}^{2}\pm 2ab+{b}^{2}$

where $a=\sin \theta$ and $b=\cos \theta$ . Part of being successful in mathematics is the ability to recognize patterns. While the terms or symbols may change, the algebra remains consistent.

Try It

Establish the identity: ${\cos }^{4}\theta -{\sin }^{4}\theta =\cos \left(2\theta \right)$ .

Show Solution

${\cos }^{4}\theta -{\sin }^{4}\theta =\left({\cos }^{2}\theta +{\sin }^{2}\theta \right)\left({\cos }^{2}\theta -{\sin }^{2}\theta \right)=\cos \left(2\theta \right)$

Example 4: Verifying a Double-Angle Identity for Tangent

Verify the identity:

$\tan \left(2\theta \right)=\frac{2}{\cot \theta -\tan \theta }$

Show Solution

In this case, we will work with the left side of the equation and simplify or rewrite until it equals the right side of the equation.

$\begin{align}\tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }&& \text{Double-angle formula} \\ &=\frac{2\tan \theta \left(\frac{1}{\tan \theta }\right)}{\left(1-{\tan }^{2}\theta \right)\left(\frac{1}{\tan \theta }\right)}&& \text{Multiply by a term that results in desired numerator}. \\ &=\frac{2}{\frac{1}{\tan \theta }-\frac{{\tan }^{2}\theta }{\tan \theta }} \\ &=\frac{2}{\cot \theta -\tan \theta }&& \text{Use reciprocal identity for }\frac{1}{\tan \theta }.\end{align}$

Analysis of the Solution

Here is a case where the more complicated side of the initial equation appeared on the right, but we chose to work the left side. However, if we had chosen the left side to rewrite, we would have been working backwards to arrive at the equivalency. For example, suppose that we wanted to show

$\frac{2\tan \theta }{1-{\tan }^{2}\theta }=\frac{2}{\cot \theta -\tan \theta }$

Let’s work on the right side.

$\begin{align}\frac{2}{\cot \theta -\tan \theta }&=\frac{2}{\frac{1}{\tan \theta }-\tan \theta }\left(\frac{\tan \theta }{\tan \theta }\right) \\ &=\frac{2\tan \theta }{\frac{1}{\cancel{\tan \theta }}\left(\cancel{\tan \theta }\right)-\tan \theta \left(\tan \theta \right)} \\ &=\frac{2\tan \theta }{1-{\tan }^{2}\theta } \end{align}$

When using the identities to simplify a trigonometric expression or solve a trigonometric equation, there are usually several paths to a desired result. There is no set rule as to what side should be manipulated. However, we should begin with the guidelines set forth earlier.

Try It

Verify the identity: $\cos \left(2\theta \right)\cos \theta ={\cos }^{3}\theta -\cos \theta {\sin }^{2}\theta$ .

Show Solution

$\cos \left(2\theta \right)\cos \theta =\left({\cos }^{2}\theta -{\sin }^{2}\theta \right)\cos \theta ={\cos }^{3}\theta -\cos \theta {\sin }^{2}\theta$

Use Reduction Formulas to Simplify an Expression

The double-angle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.

We can use two of the three double-angle formulas for cosine to derive the reduction formulas for sine and cosine. Let’s begin with $\cos \left(2\theta \right)=1 - 2{\sin }^{2}\theta$ . Solve for ${\sin }^{2}\theta :$

$\begin{gathered}\cos \left(2\theta \right)=1 - 2{\sin }^{2}\theta \\ 2{\sin }^{2}\theta =1-\cos \left(2\theta \right) \\ {\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2} \end{gathered}$

Next, we use the formula $\cos \left(2\theta \right)=2{\cos }^{2}\theta -1$ . Solve for ${\cos }^{2}\theta :$

$\begin{gathered}\cos \left(2\theta \right)=2{\cos }^{2}\theta -1 \\ 1+\cos \left(2\theta \right)=2{\cos }^{2}\theta \\ \frac{1+\cos \left(2\theta \right)}{2}={\cos }^{2}\theta \end{gathered}$

The last reduction formula is derived by writing tangent in terms of sine and cosine:

$\begin{align}{\tan }^{2}\theta &=\frac{{\sin }^{2}\theta }{{\cos }^{2}\theta } \\ &=\frac{\frac{1-\cos \left(2\theta \right)}{2}}{\frac{1+\cos \left(2\theta \right)}{2}}&& \text{Substitute the reduction formulas.} \\ &=\left(\frac{1-\cos \left(2\theta \right)}{2}\right)\left(\frac{2}{1+\cos \left(2\theta \right)}\right) \\ &=\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \end{align}$

A General Note: Reduction Formulas

The reduction formulas are summarized as follows:

$\begin{align}&{\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2} \\ &{\cos }^{2}\theta =\frac{1+\cos \left(2\theta \right)}{2} \\ &{\tan }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \end{align}$

Example 5: Writing an Equivalent Expression Not Containing Powers Greater Than 1

Write an equivalent expression for ${\cos }^{4}x$ that does not involve any powers of sine or cosine greater than 1.

Show Solution

We will apply the reduction formula for cosine twice.

$\begin{align}{\cos }^{4}x&={\left({\cos }^{2}x\right)}^{2} \\ &={\left(\frac{1+\cos \left(2x\right)}{2}\right)}^{2}&& {\text{Substitute reduction formula for cos}}^{2}x. \\ &=\frac{1}{4}\left(1+2\cos \left(2x\right)+{\cos }^{2}\left(2x\right)\right) \\ &=\frac{1}{4}+\frac{1}{2}\cos \left(2x\right)+\frac{1}{4}\left(\frac{1+\cos \left(2\left(2x\right)\right)}{2}\right) && {\text{ Substitute reduction formula for cos}}^{2}x. \\ &=\frac{1}{4}+\frac{1}{2}\cos \left(2x\right)+\frac{1}{8}+\frac{1}{8}\cos \left(4x\right) \\ &=\frac{3}{8}+\frac{1}{2}\cos \left(2x\right)+\frac{1}{8}\cos \left(4x\right) \end{align}$

Analysis of the Solution

The solution is found by using the reduction formula twice, as noted, and the perfect square formula from algebra.

Example 6: Using the Power-Reducing Formulas to Prove an Identity

Use the power-reducing formulas to prove

${\sin }^{3}\left(2x\right)=\left[\frac{1}{2}\sin \left(2x\right)\right]\left[1-\cos \left(4x\right)\right]$

Show Solution

We will work on simplifying the left side of the equation:

$\begin{align}{\sin }^{3}\left(2x\right)&=\left[\sin \left(2x\right)\right]\left[{\sin }^{2}\left(2x\right)\right] \\ &=\sin \left(2x\right)\left[\frac{1-\cos \left(4x\right)}{2}\right]&& \text{Substitute the power-reduction formula}. \\ &=\sin \left(2x\right)\left(\frac{1}{2}\right)\left[1-\cos \left(4x\right)\right] \\ &=\frac{1}{2}\left[\sin \left(2x\right)\right]\left[1-\cos \left(4x\right)\right] \end{align}$

Analysis of the Solution

Note that in this example, we substituted

$\frac{1-\cos \left(4x\right)}{2}$

for ${\sin }^{2}\left(2x\right)$ . The formula states

${\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2}$

We let $\theta =2x$ , so $2\theta =4x$ .

Try It

Use the power-reducing formulas to prove that $10{\cos }^{4}x=\frac{15}{4}+5\cos \left(2x\right)+\frac{5}{4}\cos \left(4x\right)$ .

Show Solution

$\begin{align}10{\cos }^{4}x&=10{\left({\cos }^{2}x\right)}^{2} \\ &=10{\left[\frac{1+\cos \left(2x\right)}{2}\right]}^{2}&& {\text{Substitute reduction formula for cos}}^{2}x. \\ &=\frac{10}{4}\left[1+2\cos \left(2x\right)+{\cos }^{2}\left(2x\right)\right] \\ &=\frac{10}{4}+\frac{10}{2}\cos \left(2x\right)+\frac{10}{4}\left(\frac{1+\cos\left( 2\left(2x\right)\right)}{2}\right)&& {\text{Substitute reduction formula for cos}}^{2}x. \\ &=\frac{10}{4}+\frac{10}{2}\cos \left(2x\right)+\frac{10}{8}+\frac{10}{8}\cos \left(4x\right) \\ &=\frac{30}{8}+5\cos \left(2x\right)+\frac{10}{8}\cos \left(4x\right) \\ &=\frac{15}{4}+5\cos \left(2x\right)+\frac{5}{4}\cos \left(4x\right) \end{align}$

Try It

Using Half-Angle Formulas to Find Exact Values

The next set of identities is the set of half-angle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. If we replace $\theta$ with $\frac{\alpha }{2}$ , the half-angle formula for sine is found by simplifying the equation and solving for $\sin \left(\frac{\alpha }{2}\right)$ . Note that the half-angle formulas are preceded by a $\pm$ sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which $\frac{\alpha }{2}$ terminates.

The half-angle formula for sine is derived as follows:

$\begin{align}{\sin }^{2}\theta &=\frac{1-\cos \left(2\theta \right)}{2}\\ {\sin }^{2}\left(\frac{\alpha }{2}\right)&=\frac{1-\left(\cos 2\cdot \frac{\alpha }{2}\right)}{2} \\ &=\frac{1-\cos \alpha }{2} \\ \sin \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \end{align}$

To derive the half-angle formula for cosine, we have

$\begin{align}{\cos }^{2}\theta &=\frac{1+\cos \left(2\theta \right)}{2}\\ {\cos }^{2}\left(\frac{\alpha }{2}\right)&=\frac{1+\cos \left(2\cdot \frac{\alpha }{2}\right)}{2} \\ &=\frac{1+\cos \alpha }{2} \\ \cos \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \end{align}$

For the tangent identity, we have

$\begin{align}{\tan }^{2}\theta &=\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \\ {\tan }^{2}\left(\frac{\alpha }{2}\right)&=\frac{1-\cos \left(2\cdot \frac{\alpha }{2}\right)}{1+\cos \left(2\cdot \frac{\alpha }{2}\right)} \\ &=\frac{1-\cos \alpha }{1+\cos \alpha }\hfill \\ \tan \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \end{align}$

A General Note: Half-Angle Formulas

The half-angle formulas are as follows:

$\begin{align}\sin \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \\ \text{ } \\ \cos \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \\ \text{ } \\ \tan \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \\ &=\frac{\sin \alpha }{1+\cos \alpha } \\ &=\frac{1-\cos \alpha }{\sin \alpha }\end{align}$

Example 7: Using a Half-Angle Formula to Find the Exact Value of a Sine Function

Find $\sin \left({15}^{\circ }\right)$ using a half-angle formula.

Show Solution

Since ${15}^{\circ }=\frac{{30}^{\circ }}{2}$ , we use the half-angle formula for sine:

$\begin{align} \sin \frac{{30}^{\circ }}{2}&=\sqrt{\frac{1-\cos {30}^{\circ }}{2}} \\ &=\sqrt{\frac{1-\frac{\sqrt{3}}{2}}{2}} \\ &=\sqrt{\frac{\frac{2-\sqrt{3}}{2}}{2}} \\ &=\sqrt{\frac{2-\sqrt{3}}{4}} \\ &=\frac{\sqrt{2-\sqrt{3}}}{2} \end{align}$

Analysis of the Solution

Notice that we used only the positive root because $\sin \left({15}^{\text{o}}\right)$ is positive.

How To: Given the tangent of an angle and the quadrant in which the angle lies, find the exact values of trigonometric functions of half of the angle.

Draw a triangle to represent the given information.
Determine the correct half-angle formula.
Substitute values into the formula based on the triangle.
Simplify.

Example 8: Finding Exact Values Using Half-Angle Identities

Given that $\tan \alpha =\frac{8}{15}$ and $\alpha$ lies in quadrant III, find the exact value of the following:

$\sin \left(\frac{\alpha }{2}\right)$
$\cos \left(\frac{\alpha }{2}\right)$
$\tan \left(\frac{\alpha }{2}\right)$

Show Solution

Using the given information, we can draw the triangle shown in Figure 3. Using the Pythagorean Theorem, we find the hypotenuse to be 17. Therefore, we can calculate $\sin \alpha =-\frac{8}{17}$ and $\cos \alpha =-\frac{15}{17}$ .

Diagram of a triangle in the x,y-plane. The vertices are at the origin, (-15,0), and (-15,-8). The angle at the origin is alpha. The angle formed by the side (-15,-8) to (-15,0) forms a right angle with the x axis. The hypotenuse across from the right angle is length 17.

Figure 3

Before we start, we must remember that, if $\alpha$ is in quadrant III, then $180^\circ <\alpha <270^\circ$ , so $\frac{180^\circ }{2}<\frac{\alpha }{2}<\frac{270^\circ }{2}$ . This means that the terminal side of $\frac{\alpha }{2}$ is in quadrant II, since $90^\circ <\frac{\alpha }{2}<135^\circ$ .To find $\sin \frac{\alpha }{2}$ , we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle in Figure 3 and simplify.
$\begin{align} \sin \frac{\alpha }{2}&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \\ &=\pm \sqrt{\frac{1-\left(-\frac{15}{17}\right)}{2}} \\ &=\pm \sqrt{\frac{\frac{32}{17}}{2}} \\ &=\pm \sqrt{\frac{32}{17}\cdot \frac{1}{2}} \\ &=\pm \sqrt{\frac{16}{17}} \\ &=\pm \frac{4}{\sqrt{17}} \\ &=\frac{4\sqrt{17}}{17} \end{align}$

We choose the positive value of $\sin \frac{\alpha }{2}$ because the angle terminates in quadrant II and sine is positive in quadrant II.
To find $\cos \frac{\alpha }{2}$ , we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle in Figure 3, and simplify.
$\begin{align} \cos \frac{\alpha }{2}&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \\ &=\pm \sqrt{\frac{1+\left(-\frac{15}{17}\right)}{2}} \\ &=\pm \sqrt{\frac{\frac{2}{17}}{2}} \\ &=\pm \sqrt{\frac{2}{17}\cdot \frac{1}{2}} \\ &=\pm \sqrt{\frac{1}{17}} \\ &=-\frac{\sqrt{17}}{17}\end{align}$

We choose the negative value of $\cos \frac{\alpha }{2}$ because the angle is in quadrant II because cosine is negative in quadrant II.
To find $\tan \frac{\alpha }{2}$ , we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle in Figure 3 and simplify.
$\begin{align} \tan \frac{\alpha }{2}&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \\ &=\pm \sqrt{\frac{1-\left(-\frac{15}{17}\right)}{1+\left(-\frac{15}{17}\right)}} \\ &=\pm \sqrt{\frac{\frac{32}{17}}{\frac{2}{17}}} \\ &=\pm \sqrt{\frac{32}{2}} \\ &=-\sqrt{16} \\ &=-4 \end{align}$

We choose the negative value of $\tan \frac{\alpha }{2}$ because $\frac{\alpha }{2}$ lies in quadrant II, and tangent is negative in quadrant II.

Try It

Given that $\sin \alpha =-\frac{4}{5}$ and $\alpha$ lies in quadrant IV, find the exact value of $\cos \left(\frac{\alpha }{2}\right)$ .

Show Solution

$-\frac{2}{\sqrt{5}}$

Try It

Example 9: Finding the Measurement of a Half Angle

Now, we will return to the problem posed at the beginning of the section. A bicycle ramp is constructed for high-level competition with an angle of $\theta$ formed by the ramp and the ground. Another ramp is to be constructed half as steep for novice competition. If $\tan \theta =\frac{5}{3}$ for higher-level competition, what is the measurement of the angle for novice competition?

Show Solution

Since the angle for novice competition measures half the steepness of the angle for the high level competition, and $\tan \theta =\frac{5}{3}$ for high competition, we can find $\cos \theta$ from the right triangle and the Pythagorean theorem so that we can use the half-angle identities.

$\begin{gathered}{3}^{2}+{5}^{2}=34 \\ c=\sqrt{34} \end{gathered}$

Image of a right triangle with sides 3, 5, and rad34. Rad 34 is the hypotenuse, and 3 is the base. The angle formed by the hypotenuse and base is theta. The angle between the side of length 3 and side of length 5 is a right angle.

Figure 4

We see that $\cos \theta =\frac{3}{\sqrt{34}}=\frac{3\sqrt{34}}{34}$ . We can use the half-angle formula for tangent: $\tan \frac{\theta }{2}=\sqrt{\frac{1-\cos \theta }{1+\cos \theta }}$ . Since $\tan \theta$ is in the first quadrant, so is $\tan \frac{\theta }{2}$ . Thus,

$\begin{align} \tan \frac{\theta }{2}&=\sqrt{\frac{1-\frac{3\sqrt{34}}{34}}{1+\frac{3\sqrt{34}}{34}}} \\ &=\sqrt{\frac{\frac{34 - 3\sqrt{34}}{34}}{\frac{34+3\sqrt{34}}{34}}} \\ &=\sqrt{\frac{34 - 3\sqrt{34}}{34+3\sqrt{34}}} \\ &\approx 0.57\end{align}$

We can take the inverse tangent to find the angle: ${\tan }^{-1}\left(0.57\right)\approx {29.7}^{\circ }$ . So the angle of the ramp for novice competition is $\approx {29.7}^{\circ }$ .

Key Equations

Double-angle formulas	$\begin{align}\sin \left(2\theta \right)&=2\sin \theta \cos \theta\\\text{ }\\ \cos \left(2\theta \right)&={\cos }^{2}\theta -{\sin }^{2}\theta \\ &=1 - 2{\sin }^{2}\theta \\ &=2{\cos }^{2}\theta -1 \\\text{ }\\ \tan \left(2\theta \right)&=\frac{2\tan \theta }{1-{\tan }^{2}\theta }\end{align}$
Reduction formulas	$\begin{align}&{\sin }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{2} \\ &{\cos }^{2}\theta =\frac{1+\cos \left(2\theta \right)}{2} \\ &{\tan }^{2}\theta =\frac{1-\cos \left(2\theta \right)}{1+\cos \left(2\theta \right)} \end{align}$
Half-angle formulas	$\begin{align}\sin \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{2}} \\ \text{ } \\ \cos \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1+\cos \alpha }{2}} \\ \text{ } \\ \tan \left(\frac{\alpha }{2}\right)&=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }} \\ &=\frac{\sin \alpha }{1+\cos \alpha } \\ &=\frac{1-\cos \alpha }{\sin \alpha }\end{align}$

Key Concepts

Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent.
Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term.
Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not.

Glossary

double-angle formulas: identities derived from the sum formulas for sine, cosine, and tangent in which the angles are equal

half-angle formulas: identities derived from the reduction formulas and used to determine half-angle values of trigonometric functions

reduction formulas: identities derived from the double-angle formulas and used to reduce the power of a trigonometric function

^nbsp;

Section 5.3 Homework Exercises

1. Explain how to determine the reduction identities from the double-angle identity $\cos \left(2x\right)={\cos }^{2}x-{\sin }^{2}x$ .

2. Explain how to determine the double-angle formula for $\tan \left(2x\right)$ using the double-angle formulas for $\cos \left(2x\right)$ and $\sin \left(2x\right)$ .

3. We can determine the half-angle formula for $\tan \left(\frac{x}{2}\right)=\frac{\sqrt{1-\cos x}}{\sqrt{1+\cos x}}$ by dividing the formula for $\sin \left(\frac{x}{2}\right)$ by $\cos \left(\frac{x}{2}\right)$ . Explain how to determine two formulas for $\tan \left(\frac{x}{2}\right)$ that do not involve any square roots.

4. For the half-angle formula given in the previous exercise for $\tan \left(\frac{x}{2}\right)$ , explain why dividing by 0 is not a concern. (Hint: examine the values of $\cos x$ necessary for the denominator to be 0.)

For the following exercises, find the exact values of a) $\sin \left(2x\right)$ , b) $\cos \left(2x\right)$ , and c) $\tan \left(2x\right)$ without solving for $x$ .

5. If $\sin x=\frac{1}{8}$ , and $x$ is in quadrant I.

6. If $\cos x=\frac{2}{3}$ , and $x$ is in quadrant I.

7. If $\cos x=-\frac{1}{2}$ , and $x$ is in quadrant III.

8. If $\tan x=-8$ , and $x$ is in quadrant IV.

For the following exercises, find the values of the six trigonometric functions if the conditions provided hold.

9. $\cos \left(2\theta \right)=\frac{3}{5}$ and ${90}^{\circ }\le \theta \le {180}^{\circ }$

10. $\cos \left(2\theta \right)=\frac{1}{\sqrt{2}}$ and ${180}^{\circ }\le \theta \le {270}^{\circ }$

For the following exercises, simplify to one trigonometric expression.

11. $2\sin \left(\frac{\pi }{4}\right)2\cos \left(\frac{\pi }{4}\right)$

12. $4\sin \left(\frac{\pi }{8}\right)\cos \left(\frac{\pi }{8}\right)$

For the following exercises, find the exact value using half-angle formulas.

13. $\sin \left(\frac{\pi }{8}\right)$

14. $\cos \left(-\frac{11\pi }{12}\right)$

15. $\sin \left(\frac{11\pi }{12}\right)$

16. $\cos \left(\frac{7\pi }{8}\right)$

17. $\tan \left(\frac{5\pi }{12}\right)$

18. $\tan \left(-\frac{3\pi }{12}\right)$

19. $\tan \left(-\frac{3\pi }{8}\right)$

For the following exercises, find the exact values of a) $\sin \left(\frac{x}{2}\right)$ , b) $\cos \left(\frac{x}{2}\right)$ , and c) $\tan \left(\frac{x}{2}\right)$ without solving for $x$ .

20. If $\tan x=-\frac{4}{3}$ , and $x$ is in quadrant IV.

21. If $\sin x=-\frac{12}{13}$ , and $x$ is in quadrant III.

22. If $\csc x=7$ , and $x$ is in quadrant II.

23. If $\sec x=-4$ , and $x$ is in quadrant II.

For the following exercises, use Figure 5 to find the requested half and double angles.

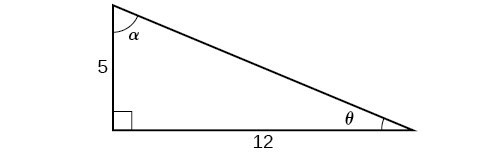
Image of a right triangle. The base is length 12, and the height is length 5. The angle between the base and the height is 90 degrees, the angle between the base and the hypotenuse is theta, and the angle between the height and the hypotenuse is alpha degrees.

Figure 5

24. Find $\sin \left(2\theta \right),\cos \left(2\theta \right)$ , and $\tan \left(2\theta \right)$ .

25. Find $\sin \left(2\alpha \right),\cos \left(2\alpha \right)$ , and $\tan \left(2\alpha \right)$ .

26. Find $\sin \left(\frac{\theta }{2}\right),\cos \left(\frac{\theta }{2}\right)$ , and $\tan \left(\frac{\theta }{2}\right)$ .

27. Find $\sin \left(\frac{\alpha }{2}\right),\cos \left(\frac{\alpha }{2}\right)$ , and $\tan \left(\frac{\alpha }{2}\right)$ .

For the following exercises, simplify each expression. Do not evaluate.

28. ${\cos }^{2}\left({28}^{\circ }\right)-{\sin }^{2}\left({28}^{\circ }\right)$

29. $2{\cos }^{2}\left({37}^{\circ }\right)-1$

30. $1 - 2{\sin }^{2}\left({17}^{\circ }\right)$

31. ${\cos }^{2}\left(9x\right)-{\sin }^{2}\left(9x\right)$

32. $4\sin \left(8x\right)\cos \left(8x\right)$

33. $6\sin \left(5x\right)\cos \left(5x\right)$

For the following exercises, prove the identity given.

34. ${\left(\sin t-\cos t\right)}^{2}=1-\sin \left(2t\right)$

35. $\sin \left(2x\right)=-2\sin \left(-x\right)\cos \left(-x\right)$

36. $\cot x-\tan x=2\cot \left(2x\right)$

37. $\frac{\sin \left(2\theta \right)}{1+\cos \left(2\theta \right)}{\tan }^{2}\theta =\tan \theta$

For the following exercises, rewrite the expression with an exponent no higher than 1.

38. ${\cos }^{2}\left(5x\right)$

39. ${\cos }^{2}\left(6x\right)$

40. ${\sin }^{4}\left(8x\right)$

41. ${\sin }^{4}\left(3x\right)$

42. ${\cos }^{2}x{\sin }^{4}x$

43. ${\cos }^{4}x{\sin }^{2}x$

44. ${\tan }^{2}x{\sin }^{2}x$

For the following exercises, reduce the equations to powers of one, and then check the answer graphically.

45. ${\tan }^{4}x$

46. ${\sin }^{2}\left(2x\right)$

47. ${\sin }^{2}x{\cos }^{2}x$

48. ${\tan }^{2}x\sin x$

49. ${\tan }^{4}x{\cos }^{2}x$

50. ${\cos }^{2}x\sin \left(2x\right)$

51. ${\cos }^{2}\left(2x\right)\sin x$

52. ${\tan }^{2}\left(\frac{x}{2}\right)\sin x$

For the following exercises, algebraically find an equivalent function, only in terms of $\sin x$ and/or $\cos x$ , and then check the answer by graphing both equations.

53. $\sin \left(4x\right)$

54. $\cos \left(4x\right)$

For the following exercises, prove the identities.

55. $\sin \left(2x\right)=\frac{2\tan x}{1+{\tan }^{2}x}$

56. $\cos \left(2\alpha \right)=\frac{1-{\tan }^{2}\alpha }{1+{\tan }^{2}\alpha }$

57. $\tan \left(2x\right)=\frac{2\sin x\cos x}{2{\cos }^{2}x - 1}$

58. ${\left({\sin }^{2}x - 1\right)}^{2}=\cos \left(2x\right)+{\sin }^{4}x$

59. $\sin \left(3x\right)=3\sin x{\cos }^{2}x-{\sin }^{3}x$

60. $\cos \left(3x\right)={\cos }^{3}x - 3{\sin }^{2}x\cos x$

61. $\frac{1+\cos \left(2t\right)}{\sin \left(2t\right)-\cos t}=\frac{2\cos t}{2\sin t - 1}$

62. $\sin \left(16x\right)=16\sin x\cos x\cos \left(2x\right)\cos \left(4x\right)\cos \left(8x\right)$

63. $\cos \left(16x\right)=\left({\cos }^{2}\left(4x\right)-{\sin }^{2}\left(4x\right)-\sin \left(8x\right)\right)\left({\cos }^{2}\left(4x\right)-{\sin }^{2}\left(4x\right)+\sin \left(8x\right)\right)$

Chapter 5: Trigonometric Identities and Equations