LEARNING OBJECTIVES
By the end of this lesson, you will be able to:
- Determine whether a function is one-to-one.
- Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
- Find or evaluate the inverse of a function.
- Use the graph of a one-to-one function to graph its inverse function on the same axes.
Determining Whether a Function is One-to-One
Some functions have only one input value for each output value, as well as having only one output for each input. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents, as listed in.
| Letter grade | Grade point average |
|---|---|
| A | 4.0 |
| B | 3.0 |
| C | 2.0 |
| D | 1.0 |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, let’s look again at the two simple functions sketched in (a)and (b) of Figure 10.

Figure 10
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
A General Note: One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.
Example 1: determining if a set of ordered pairs is a one-to-one function
For each set of ordered pairs, determine if it represents a function and, if so, if the function is one-to-one.
a) [latex]\{(-3,27),(-2,8),(-1,1),(0,0),(1,1),(2,8),(3,27)\}[/latex]
b) [latex]\{(0,0),(1,1),(4,2),(9,3),(16,4)\}[/latex]
Solution
a) Each x-value is matched with only one y-value. So this relation is a function. But each y-value is not paired with only one x-value, [latex](-3,27)[/latex] and [latex](3,27)[/latex], for example. So this function is not one-to-one.
b) Each x-value is matched with only one y-value. So this relation is a function. Since each y-value is paired with only one x-value, this function is one-to-one.
Try It 1
For each set of ordered pairs, determine if it represents a function and, if so, if the function is one-to-one.
a) [latex]\{(-3,-6),(-2,-4),(-1,-2),(0,0),(1,2),(2,4),(3,6)\}[/latex]
b) [latex]\{(-4,-8),(-2,4),(-1,2),(0,0),(1,2),(2,4),(4,8)\}[/latex]
To help us determine whether a function is one-to-one, we use the horizontal line test. We use a horizontal line and check that each horizontal line intersects the graph in only one point. The horizontal line is representing a y-value and we check that it intersects the graph in only one x-value. If every horizontal line intersects the graph of a function in at most one point, it is a one-to-one function. This is the horizontal line test.
Using the Horizontal Line Test
Once we have determined that a graph defines a function, an easy way to determine if it is a one-to-one function is to use the horizontal line test. Draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function.
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, determine that the function is not one-to-one.
Example 2: Applying the Horizontal Line Test
Consider the functions (a), (b), and (c) shown in the graphs in Figure 1.
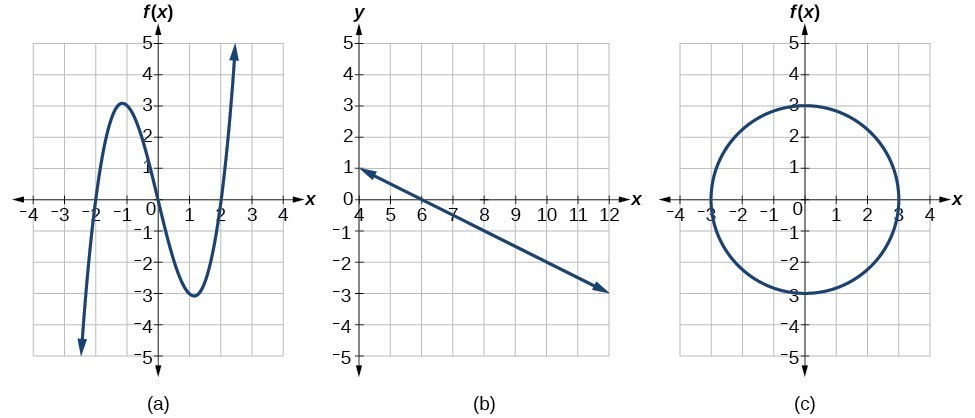
Figure 1
Are either of the functions one-to-one?
Inverse Function
Suppose [latex]y=f\left(x\right)[/latex] is a one-to-one function. An inverse function is a function for which the input of the original function becomes the output of the inverse function and the output of the original function becomes the input of the inverse function. The symbol [latex]{f}^{-1}\left(x\right)[/latex] is used to represent the inverse function of [latex]f[/latex]. In other words, if [latex]y=f\left(x\right)[/latex] is a one-to-one function, then [latex]f[/latex] has an inverse function [latex]{f}^{-1}\left(x\right)[/latex] and [latex]x={f}^{-1}\left(y\right)[/latex] .
The raised [latex]-1[/latex] is part of the notation. It is not an exponent; it does not imply a power of [latex]-1[/latex] . In other words, [latex]{f}^{-1}\left(x\right)[/latex] does not mean [latex]\frac{1}{f\left(x\right)}[/latex] because [latex]\frac{1}{f\left(x\right)}[/latex] is the reciprocal of [latex]f[/latex] and not the inverse.
Verifying an inverse function
[latex]f[/latex] and [latex]g[/latex] are inverses of each other if:
[latex]f\left(g\left(x\right)\right)=x[/latex] where [latex]x[/latex] is in the domain of [latex]f[/latex]
[latex]g\left(f\left(x\right)\right)=x[/latex] where [latex]x[/latex] is in the domain of [latex]g[/latex]
Given a function [latex]f\left(x\right)[/latex], we can verify whether some other function [latex]g\left(x\right)[/latex] is the inverse of [latex]f\left(x\right)[/latex] by checking whether either [latex]g\left(f\left(x\right)\right)=x[/latex] or [latex]f\left(g\left(x\right)\right)=x[/latex] is true. We can test whichever equation is more convenient to work with because they are logically equivalent (that is, if one is true, then so is the other.)
For example, [latex]y=4x[/latex] and [latex]y=\frac{1}{4}x[/latex] are inverse functions.
and
A few coordinate pairs from the graph of the function [latex]y=4x[/latex] are (−2, −8), (0, 0), and (2, 8). A few coordinate pairs from the graph of the function [latex]y=\frac{1}{4}x[/latex] are (−8, −2), (0, 0), and (8, 2). If we interchange the input and output of each coordinate pair of a function, the interchanged coordinate pairs would appear on the graph of the inverse function.
Example 3: Identifying an Inverse Function for a Given Input-Output Pair
If for a particular one-to-one function [latex]f\left(2\right)=4[/latex] and [latex]f\left(5\right)=12[/latex], what are the corresponding input and output values for the inverse function?
Solution
The inverse function reverses the input and output quantities, so if
[latex]\begin{align}f\left(2\right)=4,\text{ then }{f}^{-1}\left(4\right)=2;\\ f\left(5\right)=12,{\text{ then f}}^{-1}\left(12\right)=5\end{align}[/latex]
Alternatively, if we want to name the inverse function [latex]g[/latex], then [latex]g\left(4\right)=2[/latex] and [latex]g\left(12\right)=5[/latex].
Try It 2
Given that [latex]{h}^{-1}\left(6\right)=2[/latex], what are the corresponding input and output values of the original function [latex]h?[/latex]
How To: Given two functions [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex], test whether the functions are inverses of each other.
- Determine whether [latex]f\left(g\left(x\right)\right)=x[/latex] or [latex]g\left(f\left(x\right)\right)=x[/latex].
- If either statement is true, then both are true, and [latex]g={f}^{-1}[/latex] and [latex]f={g}^{-1}[/latex]. If either statement is false, then both are false, and [latex]g\ne {f}^{-1}[/latex] and [latex]f\ne {g}^{-1}[/latex].
Example 4: Testing Inverse Relationships Algebraically
If [latex]f\left(x\right)=\frac{1}{x+2}[/latex] and [latex]g\left(x\right)=\frac{1}{x}-2[/latex], is [latex]g={f}^{-1}?[/latex]
Solution
[latex]\begin{align} g\left(f\left(x\right)\right)=\frac{1}{\left(\frac{1}{x+2}\right)}{-2 }\hfill\\={ x }+{ 2 } -{ 2 }\hfill\\={ x }\hfill\end{align}[/latex]
This is enough to answer yes to the question, but we can also verify the other formula.
Analysis of the Solution
Notice the inverse operations are in reverse order of the operations from the original function.
Try It 3
If [latex]f\left(x\right)={x}^{3}-4[/latex] and [latex]g\left(x\right)=\sqrt[3]{x+4}[/latex], is [latex]g={f}^{-1}?[/latex]
Example 4: Determining Inverse Relationships for Power Functions
If [latex]f\left(x\right)={x}^{3}[/latex] (the cube function) and [latex]g\left(x\right)=\frac{1}{3}x[/latex], is [latex]g={f}^{-1}?[/latex]
Solution
[latex]f\left(g\left(x\right)\right)=\frac{{x}^{3}}{27}\ne x[/latex]
No, the functions are not inverses.
Analysis of the Solution
The correct inverse to the cube is, of course, the cube root [latex]\sqrt[3]{x}={x}^{\frac{1}{3}}[/latex], that is, the one-third is an exponent, not a multiplier.
Try It 4
If [latex]f\left(x\right)={\left(x - 1\right)}^{3}[/latex] and [latex]g\left(x\right)=\sqrt[3]{x}+1[/latex], is [latex]g={f}^{-1}?[/latex]
Finding Domain and Range of Inverse Functions
The outputs of the function [latex]f[/latex] are the inputs to [latex]{f}^{-1}[/latex], so the range of [latex]f[/latex] is also the domain of [latex]{f}^{-1}[/latex]. Likewise, because the inputs to [latex]f[/latex] are the outputs of [latex]{f}^{-1}[/latex], the domain of [latex]f[/latex] is the range of [latex]{f}^{-1}[/latex]. We can visualize the situation.

Figure 3. Domain and range of a function and its inverse
When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function. For example, the inverse of [latex]f\left(x\right)=\sqrt{x}[/latex] is [latex]{f}^{-1}\left(x\right)={x}^{2}[/latex], because a square “undoes” a square root; but the square is only the inverse of the square root on the domain [latex]\left[0,\infty \right)[/latex], since that is the range of [latex]f\left(x\right)=\sqrt{x}[/latex].
We can look at this problem from the other side, starting with the square (toolkit quadratic) function [latex]f\left(x\right)={x}^{2}[/latex]. If we want to construct an inverse to this function, we run into a problem, because for every given output of the quadratic function, there are two corresponding inputs (except when the input is 0). For example, the output 9 from the quadratic function corresponds to the inputs 3 and –3. But an output from a function is an input to its inverse; if this inverse input corresponds to more than one inverse output (input of the original function), then the “inverse” is not a function at all! To put it differently, the quadratic function is not a one-to-one function; it fails the horizontal line test, so it does not have an inverse function. In order for a function to have an inverse, it must be a one-to-one function.
In many cases, if a function is not one-to-one, we can still restrict the function to a part of its domain on which it is one-to-one. For example, we can make a restricted version of the square function [latex]f\left(x\right)={x}^{2}[/latex] with its range limited to [latex]\left[0,\infty \right)[/latex], which is a one-to-one function (it passes the horizontal line test) and which has an inverse (the square-root function).
If [latex]f\left(x\right)={\left(x - 1\right)}^{2}[/latex] on [latex]\left[1,\infty \right)[/latex], then the inverse function is [latex]{f}^{-1}\left(x\right)=\sqrt{x}+1[/latex].
- The domain of [latex]f[/latex] = range of [latex]{f}^{-1}[/latex] = [latex]\left[1,\infty \right)[/latex].
- The domain of [latex]{f}^{-1}[/latex] = range of [latex]f[/latex] = [latex]\left[0,\infty \right)[/latex].
Q & A
Is it possible for a function to have more than one inverse?
No. If two supposedly different functions, say, [latex]g[/latex] and [latex]h[/latex], both meet the definition of being inverses of another function [latex]f[/latex], then you can prove that [latex]g=h[/latex]. We have just seen that some functions only have inverses if we restrict the domain of the original function. In these cases, there may be more than one way to restrict the domain, leading to different inverses. However, on any one domain, the original function still has only one unique inverse.
A General Note: Domain and Range of Inverse Functions
The range of a function [latex]f\left(x\right)[/latex] is the domain of the inverse function [latex]{f}^{-1}\left(x\right)[/latex].
The domain of [latex]f\left(x\right)[/latex] is the range of [latex]{f}^{-1}\left(x\right)[/latex].
How To: Given a function, find the domain and range of its inverse.
- If the function is one-to-one, write the range of the original function as the domain of the inverse, and write the domain of the original function as the range of the inverse.
- If the domain of the original function needs to be restricted to make it one-to-one, then this restricted domain becomes the range of the inverse function.
Example 4: Finding the Inverses of Toolkit Functions
Identify which of the toolkit functions besides the quadratic function are not one-to-one, and find a restricted domain on which each function is one-to-one, if any. The toolkit functions are reviewed below. We restrict the domain in such a fashion that the function assumes all y-values exactly once.
| Constant | Identity | Quadratic | Cubic | Reciprocal |
| [latex]f\left(x\right)=c[/latex] | [latex]f\left(x\right)=x[/latex] | [latex]f\left(x\right)={x}^{2}[/latex] | [latex]f\left(x\right)={x}^{3}[/latex] | [latex]f\left(x\right)=\frac{1}{x}[/latex] |
| Reciprocal squared | Cube root | Square root | Absolute value | |
| [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex] | [latex]f\left(x\right)=\sqrt[3]{x}[/latex] | [latex]f\left(x\right)=\sqrt{x}[/latex] | [latex]f\left(x\right)=|x|[/latex] |
Solution
The constant function is not one-to-one, and there is no domain (except a single point) on which it could be one-to-one, so the constant function has no meaningful inverse.
The absolute value function can be restricted to the domain [latex]\left[0,\infty \right)[/latex], where it is equal to the identity function.
The reciprocal-squared function can be restricted to the domain [latex]\left(0,\infty \right)[/latex].
Analysis of the Solution
We can see that these functions (if unrestricted) are not one-to-one by looking at their graphs. They both would fail the horizontal line test. However, if a function is restricted to a certain domain so that it passes the horizontal line test, then in that restricted domain, it can have an inverse.

Figure 4. (a) Absolute value (b) Reciprocal squared
Try It 5
The domain of function [latex]f[/latex] is [latex]\left(1,\infty \right)[/latex] and the range of function [latex]f[/latex] is [latex]\left(\mathrm{-\infty },-2\right)[/latex]. Find the domain and range of the inverse function.
Finding and Evaluating Inverse Functions
Once we have a one-to-one function, we can evaluate its inverse at specific inverse function inputs or construct a complete representation of the inverse function in many cases.
Inverting Tabular Functions
Suppose we want to find the inverse of a function represented in table form. Remember that the domain of a function is the range of the inverse and the range of the function is the domain of the inverse. So we need to interchange the domain and range.
Each row (or column) of inputs becomes the row (or column) of outputs for the inverse function. Similarly, each row (or column) of outputs becomes the row (or column) of inputs for the inverse function.
Example 5: Interpreting the Inverse of a Tabular Function
A function [latex]f\left(t\right)[/latex] is given below, showing distance in miles that a car has traveled in [latex]t[/latex] minutes. Find and interpret [latex]{f}^{-1}\left(70\right)[/latex].
| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 60 | 70 |
Solution
The inverse function takes an output of [latex]f[/latex] and returns an input for [latex]f[/latex]. So in the expression [latex]{f}^{-1}\left(70\right)[/latex], 70 is an output value of the original function, representing 70 miles. The inverse will return the corresponding input of the original function [latex]f[/latex], 90 minutes, so [latex]{f}^{-1}\left(70\right)=90[/latex]. The interpretation of this is that, to drive 70 miles, it took 90 minutes.
Alternatively, recall that the definition of the inverse was that if [latex]f\left(a\right)=b[/latex], then [latex]{f}^{-1}\left(b\right)=a[/latex]. By this definition, if we are given [latex]{f}^{-1}\left(70\right)=a[/latex], then we are looking for a value [latex]a[/latex] so that [latex]f\left(a\right)=70[/latex]. In this case, we are looking for a [latex]t[/latex] so that [latex]f\left(t\right)=70[/latex], which is when [latex]t=90[/latex].
Try It 6
Using the table below, find and interpret (a) [latex]\text{ }f\left(60\right)[/latex], and (b) [latex]\text{ }{f}^{-1}\left(60\right)[/latex].
| [latex]t\text{ (minutes)}[/latex] | 30 | 50 | 60 | 70 | 90 |
| [latex]f\left(t\right)\text{ (miles)}[/latex] | 20 | 40 | 50 | 60 | 70 |
Evaluating the Inverse of a Function, Given a Graph of the Original Function
We saw in Functions and Function Notation that the domain of a function can be read by observing the horizontal extent of its graph. We find the domain of the inverse function by observing the vertical extent of the graph of the original function, because this corresponds to the horizontal extent of the inverse function. Similarly, we find the range of the inverse function by observing the horizontal extent of the graph of the original function, as this is the vertical extent of the inverse function. If we want to evaluate an inverse function, we find its input within its domain, which is all or part of the vertical axis of the original function’s graph.
How To: Given the graph of a function, evaluate its inverse at specific points.
- Find the desired input on the y-axis of the given graph.
- Read the inverse function’s output from the x-axis of the given graph.
Example 6: Evaluating a Function and Its Inverse from a Graph at Specific Points
A function [latex]g\left(x\right)[/latex] is given in Figure 5. Find [latex]g\left(3\right)[/latex] and [latex]{g}^{-1}\left(3\right)[/latex].

Figure 5
Solution
To evaluate [latex]g\left(3\right)[/latex], we find 3 on the x-axis and find the corresponding output value on the y-axis. The point [latex]\left(3,1\right)[/latex] tells us that [latex]g\left(3\right)=1[/latex].
To evaluate [latex]{g}^{-1}\left(3\right)[/latex], recall that by definition [latex]{g}^{-1}\left(3\right)[/latex] means the value of x for which [latex]g\left(x\right)=3[/latex]. By looking for the output value 3 on the vertical axis, we find the point [latex]\left(5,3\right)[/latex] on the graph, which means [latex]g\left(5\right)=3[/latex], so by definition, [latex]{g}^{-1}\left(3\right)=5[/latex].

Figure 6
Try It 7
Using the graph in Example 6, (a) find [latex]{g}^{-1}\left(1\right)[/latex], and (b) estimate [latex]{g}^{-1}\left(4\right)[/latex].
Finding Inverses of Functions Represented by Formulas
Sometimes we will need to know an inverse function for all elements of its domain, not just a few. If the original function is given as a formula— for example, [latex]y[/latex] as a function of [latex]x\text{-\hspace{0.17em}}[/latex] we can often find the inverse function by solving to obtain [latex]x[/latex] as a function of [latex]y[/latex].
How To: Given a one-to-one function represented by a formula, find the inverse.
- Replace [latex]f\left(x\right)[/latex] with [latex]y[/latex] .
- Switch [latex]x[/latex] and [latex]y[/latex].
- Solve for [latex]y[/latex]
- Replace [latex]y[/latex] with [latex]{f}^{-1}[/latex]
Example 8: Solving to Find an Inverse Function
Find the inverse of the function [latex]f\left(x\right)=\frac{2}{x - 3}+4[/latex].
Solution
Analysis of the Solution
The domain and range of [latex]f[/latex] exclude the values 3 and 4, respectively. [latex]f[/latex] and [latex]{f}^{-1}[/latex] are equal at two points but are not the same function, as we can see by creating the table below.
| [latex]x[/latex] | 1 | 2 | 5 | [latex]{f}^{-1}\left(y\right)[/latex] |
| [latex]f\left(x\right)[/latex] | 3 | 2 | 5 | [latex]y[/latex] |
Example 9: Solving to Find an Inverse with Radicals
Find the inverse of the function [latex]f\left(x\right)=2+\sqrt{x - 4}[/latex].
Solution
The domain of [latex]f[/latex] is [latex]\left[4,\infty \right)[/latex]. Notice that the range of [latex]f[/latex] is [latex]\left[2,\infty \right)[/latex], so this means that the domain of the inverse function [latex]{f}^{-1}[/latex] is also [latex]\left[2,\infty \right)[/latex].
Analysis of the Solution
The formula we found for [latex]{f}^{-1}\left(x\right)[/latex] looks like it would be valid for all real [latex]x[/latex]. However, [latex]{f}^{-1}[/latex] itself must have an inverse (namely, [latex]f[/latex] ) so we have to restrict the domain of [latex]{f}^{-1}[/latex] to [latex]\left[2,\infty \right)[/latex] in order to make [latex]{f}^{-1}[/latex] a one-to-one function. This domain of [latex]{f}^{-1}[/latex] is exactly the range of [latex]f[/latex].
Try It 8
What is the inverse of the function [latex]f\left(x\right)=2-\sqrt{x}?[/latex] State the domains of both the function and the inverse function.
Now that we can find the inverse of a function, we will explore the graphs of functions and their inverses. Let us return to the quadratic function [latex]f\left(x\right)={x}^{2}[/latex] restricted to the domain [latex]\left[0,\infty \right)[/latex], on which this function is one-to-one, and graph it as in Figure 7.

Figure 7. Quadratic function with domain restricted to [0, ∞).
Restricting the domain to [latex]\left[0,\infty \right)[/latex] makes the function one-to-one (it will obviously pass the horizontal line test), so it has an inverse on this restricted domain.
We already know that the inverse of the toolkit quadratic function is the square root function, that is, [latex]{f}^{-1}\left(x\right)=\sqrt{x}[/latex]. What happens if we graph both [latex]f\text{ }[/latex] and [latex]{f}^{-1}[/latex] on the same set of axes, using the [latex]x\text{-}[/latex] axis for the input to both [latex]f\text{ and }{f}^{-1}?[/latex]
We notice a distinct relationship: The graph of [latex]{f}^{-1}\left(x\right)[/latex] is the graph of [latex]f\left(x\right)[/latex] reflected about the diagonal line [latex]y=x[/latex], which we will call the identity line, shown in Figure 8.

Figure 8. Square and square-root functions on the non-negative domain
This relationship will be observed for all one-to-one functions, because it is a result of the function and its inverse swapping inputs and outputs. This is equivalent to interchanging the roles of the vertical and horizontal axes.
Example 10: Finding the Inverse of a Function Using Reflection about the Identity Line
Given the graph of [latex]f\left(x\right)[/latex], sketch a graph of [latex]{f}^{-1}\left(x\right)[/latex].

Figure 9
Solution
This is a one-to-one function, so we will be able to sketch an inverse. Note that the graph shown has an apparent domain of [latex]\left(0,\infty \right)[/latex] and range of [latex]\left(-\infty ,\infty \right)[/latex], so the inverse will have a domain of [latex]\left(-\infty ,\infty \right)[/latex] and range of [latex]\left(0,\infty \right)[/latex].
If we reflect this graph over the line [latex]y=x[/latex], the point [latex]\left(1,0\right)[/latex] reflects to [latex]\left(0,1\right)[/latex] and the point [latex]\left(4,2\right)[/latex] reflects to [latex]\left(2,4\right)[/latex]. Sketching the inverse on the same axes as the original graph gives us the result in Figure 10.

Figure 10. The function and its inverse, showing reflection about the identity line
Q & A
Is there any function that is equal to its own inverse?
Yes. If [latex]f={f}^{-1}[/latex], then [latex]f\left(f\left(x\right)\right)=x[/latex], and we can think of several functions that have this property. The identity function does, and so does the reciprocal function, because
Any function [latex]f\left(x\right)=c-x[/latex], where [latex]c[/latex] is a constant, is also equal to its own inverse.
Key Concepts
- A function is one-to-one if each output value corresponds to only one input value.
- The graph of a one-to-one function passes the horizontal line test.
- If [latex]g\left(x\right)[/latex] is the inverse of [latex]f\left(x\right)[/latex], then
- [latex]g\left(f\left(x\right)\right)=f\left(g\left(x\right)\right)=x[/latex].
- Each of the toolkit functions has an inverse.
- For a function to have an inverse, it must be one-to-one (pass the horizontal line test).
- A function that is not one-to-one over its entire domain may be one-to-one on part of its domain.
- For a tabular function, exchange the input and output rows to obtain the inverse.
- The inverse of a function can be determined at specific points on its graph.
- To find the inverse of a formula, solve the equation [latex]y=f\left(x\right)[/latex] for [latex]x[/latex] as a function of [latex]y[/latex]. Then exchange the labels [latex]x[/latex] and [latex]y[/latex].
- The graph of an inverse function is the reflection of the graph of the original function across the line [latex]y=x[/latex].
Glossary
- horizontal line test
- a method of testing whether a function is one-to-one by determining whether any horizontal line intersects the graph more than once
- inverse function
- for any one-to-one function [latex]f\left(x\right)[/latex], the inverse is a function [latex]{f}^{-1}\left(x\right)[/latex] such that [latex]{f}^{-1}\left(f\left(x\right)\right)=x[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex]; this also implies that [latex]f\left({f}^{-1}\left(x\right)\right)=x[/latex] for all [latex]x[/latex] in the domain of [latex]{f}^{-1}[/latex]
- one-to-one function
- a function for which each value of the output is associated with a unique input value
Section 1.10 Homework Exercises
1. How can you determine if a relation is a one-to-one function?
2. Why does the horizontal line test tell us whether the graph of a function is one-to-one?
3. Why do we restrict the domain of the function [latex]f\left(x\right)={x}^{2}[/latex] to find the function’s inverse?
4. Can a function be its own inverse? Explain.
5. Are one-to-one functions either always increasing or always decreasing? Why or why not?
6. How do you find the inverse of a function algebraically?
7. Show that the function [latex]f\left(x\right)=a-x[/latex] is its own inverse for all real numbers [latex]a[/latex].
For the following exercises, find [latex]{f}^{-1}\left(x\right)[/latex] for each function.
8. [latex]f\left(x\right)=x+3[/latex]
9. [latex]f\left(x\right)=x+5[/latex]
10. [latex]f\left(x\right)=2-x[/latex]
11. [latex]f\left(x\right)=3-x[/latex]
12. [latex]f\left(x\right)=\frac{x}{x+2}[/latex]
13. [latex]f\left(x\right)=\frac{2x+3}{5x+4}[/latex]
For the following exercises, find a domain on which each function [latex]f[/latex] is one-to-one and non-decreasing. Write the domain in interval notation. Then find the inverse of [latex]f[/latex] restricted to that domain.
14. [latex]f\left(x\right)={\left(x+7\right)}^{2}[/latex]
15. [latex]f\left(x\right)={\left(x - 6\right)}^{2}[/latex]
16. [latex]f\left(x\right)={x}^{2}-5[/latex]
17. Given [latex]f\left(x\right)=\frac{x}{2}+x[/latex] and [latex]g\left(x\right)=\frac{2x}{1-x}[/latex]
a. Find [latex]f\left(g\left(x\right)\right)[/latex] and [latex]g\left(f\left(x\right)\right)[/latex]
b. What does the answer tell us about the relationship between [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)?[/latex]
For the following exercises, use function composition to verify that [latex]f\left(x\right)[/latex] and [latex]g\left(x\right)[/latex] are inverse functions.
18. [latex]f\left(x\right)=\sqrt[3]{x - 1}[/latex] and [latex]g\left(x\right)={x}^{3}+1[/latex]
19. [latex]f\left(x\right)=-3x+5[/latex] and [latex]g\left(x\right)=\frac{x - 5}{-3}[/latex]
For the following exercises, determine if the given graph is a one-to-one function.
20. Graph of a circle.
21. Graph of a parabola.
22. Graph of a rotated cubic function.
23. Graph of half of 1/x.
24. Graph of a one-to-one function.
For the following exercises, determine whether the graph represents a one-to-one function.
25.

26.

For the following exercises, use the graph of [latex]f[/latex] shown below.

27. Find [latex]f\left(0\right)[/latex].
28. Solve [latex]f\left(x\right)=0[/latex].
29. Find [latex]{f}^{-1}\left(0\right)[/latex].
30. Solve [latex]{f}^{-1}\left(x\right)=0[/latex].
For the following exercises, use the graph of the one-to-one function shown below.

31. Sketch the graph of [latex]{f}^{-1}[/latex].
32. Find [latex]f\left(6\right)\text{ and }{f}^{-1}\left(2\right)[/latex].
33. If the complete graph of [latex]f[/latex] is shown, find the domain of [latex]f[/latex].
34. If the complete graph of [latex]f[/latex] is shown, find the range of [latex]f[/latex].
For the following exercises, evaluate or solve, assuming that the function [latex]f[/latex] is one-to-one.
35. If [latex]f\left(6\right)=7[/latex], find [latex]{f}^{-1}\left(7\right)[/latex].
36. If [latex]f\left(3\right)=2[/latex], find [latex]{f}^{-1}\left(2\right)[/latex].
37. If [latex]{f}^{-1}\left(-4\right)=-8[/latex], find [latex]f\left(-8\right)[/latex].
38. If [latex]{f}^{-1}\left(-2\right)=-1[/latex], find [latex]f\left(-1\right)[/latex].
For the following exercises, use the values listed in the table below to evaluate or solve.
| [latex]x[/latex] | [latex]f\left(x\right)[/latex] |
| 0 | 8 |
| 1 | 0 |
| 2 | 7 |
| 3 | 4 |
| 4 | 2 |
| 5 | 6 |
| 6 | 5 |
| 7 | 3 |
| 8 | 9 |
| 9 | 1 |
39. Find [latex]f\left(1\right)[/latex].
40. Solve [latex]f\left(x\right)=3[/latex].
41. Find [latex]{f}^{-1}\left(0\right)[/latex].
42. Solve [latex]{f}^{-1}\left(x\right)=7[/latex].
43. Use the tabular representation of [latex]f[/latex] to create a table for [latex]{f}^{-1}\left(x\right)[/latex].
| [latex]x[/latex] | 3 | 6 | 9 | 13 | 14 |
| [latex]f\left(x\right)[/latex] | 1 | 4 | 7 | 12 | 16 |
For the following exercises, find the inverse function. Then, graph the function and its inverse.
44. [latex]f\left(x\right)=\frac{3}{x - 2}[/latex]
45. [latex]f\left(x\right)={x}^{3}-1[/latex]
46. Find the inverse function of [latex]f\left(x\right)=\frac{1}{x - 1}[/latex]. Use a graphing utility to find its domain and range. Write the domain and range in interval notation.
47. To convert from [latex]x[/latex] degrees Celsius to [latex]y[/latex] degrees Fahrenheit, we use the formula [latex]f\left(x\right)=\frac{9}{5}x+32[/latex]. Find the inverse function, if it exists, and explain its meaning.
48. The circumference [latex]C[/latex] of a circle is a function of its radius given by [latex]C\left(r\right)=2\pi r[/latex]. Express the radius of a circle as a function of its circumference. Call this function [latex]r\left(C\right)[/latex]. Find [latex]r\left(36\pi \right)[/latex] and interpret its meaning.
49. A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time, [latex]t[/latex], in hours given by [latex]d\left(t\right)=50t[/latex]. Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function [latex]t\left(d\right)[/latex]. Find [latex]t\left(180\right)[/latex] and interpret its meaning.
Section 1.8 Solutions to Odd-Numbered Exercises
1. Each output of a function must have exactly one input for the function to be one-to-one.
3. Without any domain restriction, [latex]f(x)=x^{2}[/latex] does not have an inverse function as it fails the horizontal line test. But if we restrict the domain to be [latex]x>0[/latex], then we find that it passes the horizontal line test and therefore has an inverse function.
5. One-to-one functions are always increasing or decreasing. This ensures there is only one input for every output.
7. [latex]f(x)=a-x\\y=a-x\\x=a-y\\x+y=a\\y=a-x\\f^{-1}=a-x[/latex]
9. [latex]f^{-1}(x)=x-5[/latex]
11. [latex]f^{-1}(x)=3-x[/latex]
13. [latex]f^{-1}(x)=\frac{3-4x}{5x-2}[/latex]
15. Domain of [latex]f(x)[/latex] is [latex]\left[6,\infty \right)[/latex] and [latex]f^{-1}=\sqrt{x}+6[/latex]
17. a. [latex]f(g(x))=\frac{3x}{1-x}[/latex] and [latex]g(f(x))=\frac{6x}{2-3x}[/latex]
b. [latex]f(x)[/latex] and [latex]g(x)[/latex] are not inverses.
19. [latex]f(g(x))=x[/latex] and [latex]g(f(x))=x[/latex]
21. Not one-to-one
23. One-to-one
25. Not one-to-one
27. [latex]f(0)=3[/latex]
29. [latex]f^{-1}(0)=2[/latex]
31.

33. [latex]\left[2,\infty \right)[/latex]
35.[latex]f^{-1}(7)=6[/latex]
37. [latex]f(-8)=-4[/latex]
39. [latex]f(1)=0[/latex]
41. [latex]f^{-1}(0)=1[/latex]
43.
| [latex]x[/latex] | 1 | 4 | 7 | 12 | 16 |
| [latex]{f}^{-1}\left(x\right)[/latex] | 3 | 6 | 9 | 13 | 14 |
45. [latex]{f}^{-1}\left(x\right)={\left(1+x\right)}^{1/3}[/latex]

47. [latex]{f}^{-1}\left(x\right)=\frac{5}{9}\left(x - 32\right)[/latex]. Given the Fahrenheit temperature, [latex]x[/latex], this formula allows you to calculate the Celsius temperature.
49. [latex]t\left(d\right)=\frac{d}{50}[/latex], [latex]t\left(180\right)=\frac{180}{50}[/latex]. The time for the car to travel 180 miles is 3.6 hours.
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.

Analysis of the Solution
Notice that if we show the coordinate pairs in a table form, the input and output are clearly reversed.