Learning Outcomes
- Use right triangles to evaluate trigonometric functions.
- Find function values for 30° (π/6), 45° (π/4), and 60° (π/3).
- Use cofunctions of complementary angles.
- Use the definitions of trigonometric functions of any angle.
- Use right triangle trigonometry to solve applied problems.
Using Right Triangles to Evaluate Trigonometric Functions
In earlier sections, we used a unit circle to define the trigonometric functions. In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of [latex]t[/latex] is its value at [latex]t[/latex] radians. First, we need to create our right triangle. Figure 1 shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point [latex]\left(x,y\right)\\[/latex] to the x-axis, we have a right triangle whose vertical side has length [latex]y[/latex] and whose horizontal side has length [latex]x[/latex]. We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.
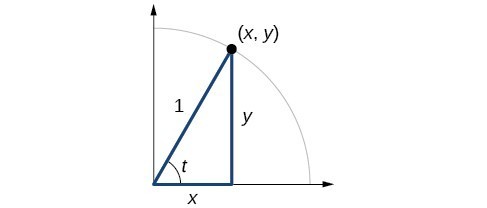
Figure 1
We know
Likewise, we know
These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using [latex]\left(x,y\right)[/latex] coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of [latex]x[/latex], we will call the side between the given angle and the right angle the adjacent side to angle [latex]t[/latex]. (Adjacent means “next to.”) Instead of [latex]y[/latex], we will call the side most distant from the given angle the opposite side from angle [latex]t[/latex]. And instead of [latex]1[/latex], we will call the side of a right triangle opposite the right angle the hypotenuse. These sides are labeled in Figure 2.
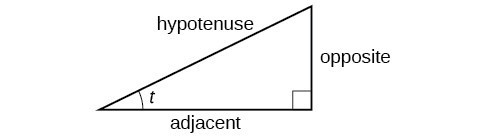
Figure 2. The sides of a right triangle in relation to angle [latex]t[/latex].
Understanding Right Triangle Relationships
Given a right triangle with an acute angle of [latex]t[/latex],
A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “Sine is opposite over hypotenuse, Cosine is adjacent over hypotenuse, Tangent is opposite over adjacent.”
How To: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle.
- Find the sine as the ratio of the opposite side to the hypotenuse
- Find the cosine as the ratio of the adjacent side to the hypotenuse.
- Find the tangent is the ratio of the opposite side to the adjacent side.
Example 1: Evaluating a Trigonometric Function of a Right Triangle
Given the triangle shown in Figure 3, find the value of [latex]\cos \alpha[/latex].
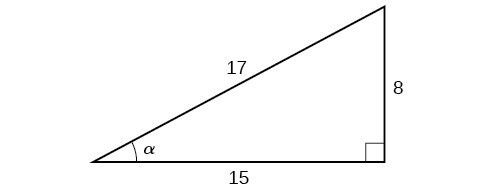
Figure 3
Try It
Given the triangle shown in Figure 4, find the value of [latex]\text{sin}t[/latex].
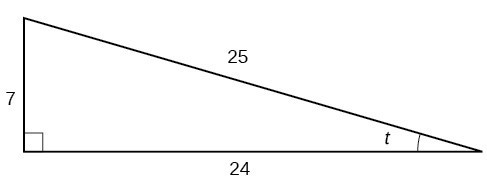
Figure 4
Relating Angles and Their Functions
When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure 5. The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.
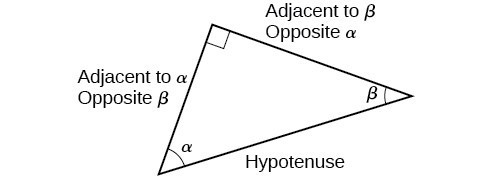
Figure 5. The side adjacent to one angle is opposite the other.
We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.
How To: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles.
- If needed, draw the right triangle and label the angle provided.
- Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
- Find the required function:
- sine as the ratio of the opposite side to the hypotenuse
- cosine as the ratio of the adjacent side to the hypotenuse
- tangent as the ratio of the opposite side to the adjacent side
- secant as the ratio of the hypotenuse to the adjacent side
- cosecant as the ratio of the hypotenuse to the opposite side
- cotangent as the ratio of the adjacent side to the opposite side
Example 2: Evaluating Trigonometric Functions of Angles Not in Standard Position
Using the triangle shown in Figure 6, evaluate [latex]\sin \alpha[/latex], [latex]\cos \alpha[/latex], [latex]\tan \alpha[/latex], [latex]\sec \alpha[/latex], [latex]\csc \alpha [/latex], and [latex]\cot \alpha[/latex].
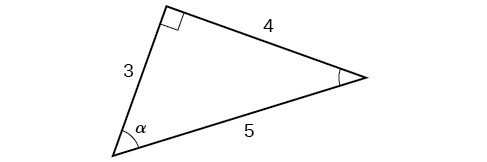
Figure 6
Try It
Using the triangle shown in Figure 7, evaluate [latex]\sin t[/latex], [latex]\cos t[/latex], [latex]\tan t[/latex], [latex]\sec t[/latex], [latex]\csc t[/latex], and [latex]\cot t[/latex].
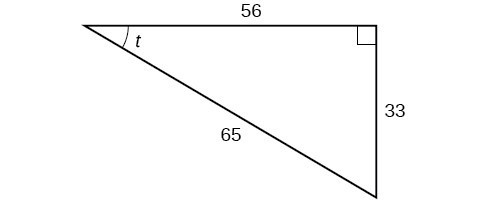
Figure 7
Try It
Finding Trigonometric Functions of Special Angles Using Side Lengths
We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of [latex]30^\circ [/latex], [latex]60^\circ [/latex], and [latex]45^\circ[/latex], however, remember that when dealing with right triangles, we are limited to angles between [latex]0^\circ \text{ and } 90^\circ[/latex].
Suppose we have a [latex]30^\circ ,60^\circ ,90^\circ [/latex] triangle, which can also be described as a [latex]\frac{\pi }{6}, \frac{\pi }{3},\frac{\pi }{2}[/latex] triangle. The sides have lengths in the relation [latex]s,\sqrt{3}s,2s[/latex]. The sides of a [latex]45^\circ ,45^\circ ,90^\circ [/latex] triangle, which can also be described as a [latex]\frac{\pi }{4},\frac{\pi }{4},\frac{\pi }{2}[/latex] triangle, have lengths in the relation [latex]s,s,\sqrt{2}s[/latex]. These relations are shown in Figure 8.
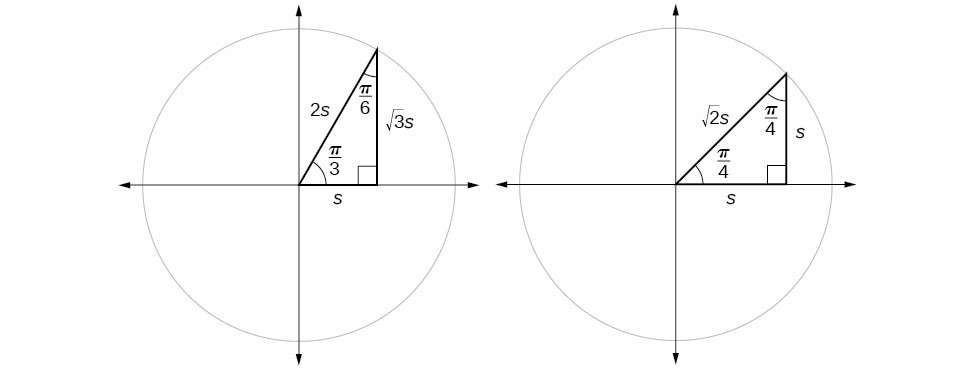
Figure 8. Side lengths of special triangles
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.
How To: Given trigonometric functions of a special angle, evaluate using side lengths.
- Use the side lengths shown in Figure 8 for the special angle you wish to evaluate.
- Use the ratio of side lengths appropriate to the function you wish to evaluate.
Example 3: Evaluating Trigonometric Functions of Special Angles Using Side Lengths
Find the exact value of the trigonometric functions of [latex]\frac{\pi }{3}[/latex], using side lengths.
Try It
Find the exact value of the trigonometric functions of [latex]\frac{\pi }{4}[/latex], using side lengths.
By looking at all six trig functions and their special angles, we can organize it all in one place.
| Angle | [latex]0[/latex] | [latex]\frac{\pi }{6},\text{ or }{30}^{\circ}[/latex] | [latex]\frac{\pi }{4},\text{ or } {45}^{\circ }[/latex] | [latex]\frac{\pi }{3},\text{ or }{60}^{\circ }[/latex] | [latex]\frac{\pi }{2},\text{ or }{90}^{\circ }[/latex] |
| Cosine | 1 | [latex]\frac{\sqrt{3}}{2}[/latex] | [latex]\frac{\sqrt{2}}{2}[/latex] | [latex]\frac{1}{2}[/latex] | 0 |
| Sine | 0 | [latex]\frac{1}{2}[/latex] | [latex]\frac{\sqrt{2}}{2}[/latex] | [latex]\frac{\sqrt{3}}{2}[/latex] | 1 |
| Tangent | 0 | [latex]\frac{\sqrt{3}}{3}[/latex] | 1 | [latex]\sqrt{3}[/latex] | Undefined |
| Secant | 1 | [latex]\frac{2\sqrt{3}}{3}[/latex] | [latex]\sqrt{2}[/latex] | 2 | Undefined |
| Cosecant | Undefined | 2 | [latex]\sqrt{2}[/latex] | [latex]\frac{2\sqrt{3}}{3}[/latex] | 1 |
| Cotangent | Undefined | [latex]\sqrt{3}[/latex] | 1 | [latex]\frac{\sqrt{3}}{3}[/latex] | 0 |
Now that we have this table, we can use it to find the exact values of trigonometric expressions.
Example 4: Evaluating Trigonometric Functions of Special Angles
Find the exact value of the trigonometric function [latex]\frac{\sin\left(\frac{\pi}{6}\right)}{1+\cos^{2}\left(\frac{\pi}{6}\right)}[/latex] using the table above.
Try It
Find the exact value of the trigonometric function [latex]\sec^{2}\left(45^\circ\right)+\tan^{2}\left(60^\circ\right)[/latex] using the table above.
Using Equal Cofunction of Complements
If we look at the table above, we will notice a pattern. In a right triangle with angles of [latex]\frac{\pi }{6}[/latex] and [latex]\frac{\pi }{3}[/latex], we see that the sine of [latex]\frac{\pi }{3}[/latex], namely [latex]\frac{\sqrt{3}}{2}[/latex], is also the cosine of [latex]\frac{\pi }{6}[/latex], while the sine of [latex]\frac{\pi }{6}[/latex], namely [latex]\frac{1}{2}[/latex], is also the cosine of [latex]\frac{\pi }{3}[/latex].
[latex]\begin{align} &\sin \frac{\pi }{3}=\cos \frac{\pi }{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ &\sin \frac{\pi }{6}=\cos \frac{\pi }{3}=\frac{s}{2s}=\frac{1}{2} \end{align}[/latex] 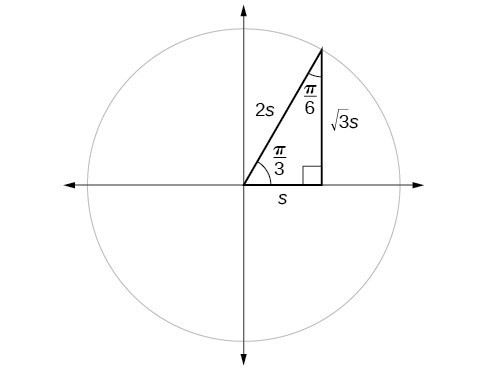
Figure 9. The sine of [latex]\frac{\pi }{3}[/latex] equals the cosine of [latex]\frac{\pi }{6}[/latex] and vice versa.
This result should not be surprising because, as we see from Figure 9, the side opposite the angle of [latex]\frac{\pi }{3}[/latex] is also the side adjacent to [latex]\frac{\pi }{6}[/latex], so [latex]\sin \left(\frac{\pi }{3}\right)[/latex] and [latex]\cos \left(\frac{\pi }{6}\right)[/latex] are exactly the same ratio of the same two sides, [latex]\sqrt{3}s[/latex] and [latex]2s[/latex]. Similarly, [latex]\cos \left(\frac{\pi }{3}\right)[/latex] and [latex]\sin \left(\frac{\pi }{6}\right)[/latex] are also the same ratio using the same two sides, [latex]s[/latex] and [latex]2s[/latex].
The interrelationship between the sines and cosines of [latex]\frac{\pi }{6}[/latex] and [latex]\frac{\pi }{3}[/latex] also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to [latex]\pi [/latex], and the right angle is [latex]\frac{\pi }{2}[/latex], the remaining two angles must also add up to [latex]\frac{\pi }{2}[/latex]. That means that a right triangle can be formed with any two angles that add to [latex]\frac{\pi }{2}[/latex] —in other words, any two complementary angles. So we may state a cofunction identity: If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure 10.
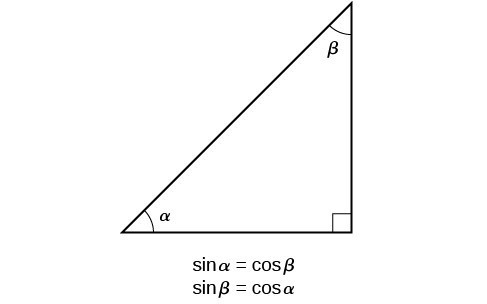
Figure 10. Cofunction identity of sine and cosine of complementary angles
Using this identity, we can state without calculating, for instance, that the sine of [latex]\frac{\pi }{12}[/latex] equals the cosine of [latex]\frac{5\pi }{12}[/latex], and that the sine of [latex]\frac{5\pi }{12}[/latex] equals the cosine of [latex]\frac{\pi }{12}[/latex]. We can also state that if, for a certain angle [latex]t[/latex], [latex]\cos \text{ }t=\frac{5}{13}[/latex], then [latex]\sin \left(\frac{\pi }{2}-t\right)=\frac{5}{13}[/latex] as well.
A General Note: Cofunction Identities
The cofunction identities in radians are listed in the table below.
| [latex]\cos t=\sin \left(\frac{\pi }{2}-t\right)[/latex] | [latex]\sin t=\cos \left(\frac{\pi }{2}-t\right)[/latex] |
| [latex]\tan t=\cot \left(\frac{\pi }{2}-t\right)[/latex] | [latex]\cot t=\tan \left(\frac{\pi }{2}-t\right)[/latex] |
| [latex]\sec t=\csc \left(\frac{\pi }{2}-t\right)[/latex] | [latex]\csc t=\sec \left(\frac{\pi }{2}-t\right)[/latex] |
How To: Given the sine and cosine of an angle, find the sine or cosine of its complement.
- To find the sine of the complementary angle, find the cosine of the original angle.
- To find the cosine of the complementary angle, find the sine of the original angle.
Example 5: Using Cofunction Identities
Write the following as an equivalent cosine expression: [latex]\sin \left(\frac{5\pi}{12}\right)[/latex].
Example 6: Using Cofunction Identities
Write the following as an equivalent tangent expression: [latex]\cot\left(25^\circ\right)[/latex].
Try It
Write the following as an equivalent cosecant expression: [latex]\sec\left(68^\circ\right)[/latex].
Using Trigonometric Functions
In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.
How To: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides.
- For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
- Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
- Using the value of the trigonometric function and the known side length, solve for the missing side length.
Example 7: Finding Missing Side Lengths Using Trigonometric Ratios
Find the unknown sides of the triangle in Figure 11.
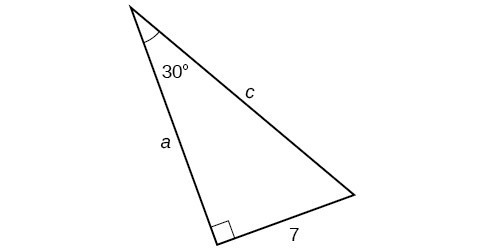
Figure 11
Try It
A right triangle has one angle of [latex]\frac{\pi }{3}[/latex] and a hypotenuse of 20. Find the unknown sides and angle of the triangle.
Try It
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer’s eye. In the figure below, [latex]\alpha[/latex] represents the angle of elevation and [latex]\beta[/latex] represents the angle of depression.

Figure 12
How To: Given a tall object, measure its height indirectly.
- Make a sketch of the problem situation to keep track of known and unknown information.
- Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
- At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
- Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
- Solve the equation for the unknown height.
Example 8: Measuring a Distance Indirectly
To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures the angle of elevation to be [latex]57^\circ [/latex], as shown in Figure 13. Find the height of the tree.
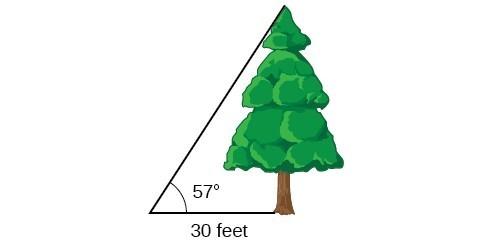
Figure 13
Try It
How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building with an angle of elevation [latex]\frac{5\pi }{12}[/latex] ? Round to the nearest foot.
Try It
Inverse Trigonometric Function on a calculator
If two sides of a right triangle are given, an inverse trigonometric function can be used to find an acute angle in a triangle. There is an inverse trig button on a calculator that appears above the normal sin, cos, tan buttons on a calculator. A shift or second key is required to select these, and they are [latex]\sin^{-1},\cos^{-1},\tan^{-1}[/latex]. The calculator will return an angle in either radians or degrees, depending on what mode your calculator is in. We will need the inverse tangent function for bearing.
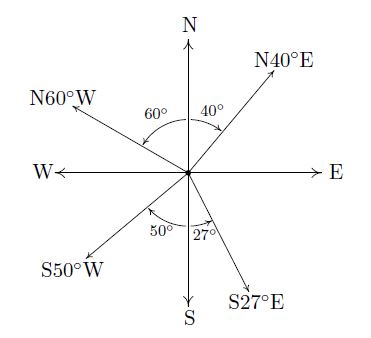
Bearing
Bearing is the direction you are heading according to a compass. On most maps, N is up, S is down, W is to the left, and E is to the right. Bearings are written in this form: (N or S)(Acute Angle)(E or W). The angle is measured from either the north or south, whichever letter comes first in your bearing. For example, [latex]N20^\circ E[/latex] means that you will go north and then go 20 degrees to the east, or to the right. The drawing below gives an example of how bearings are drawn. As you can see, each angle is measure from either the N or S depending on the first letter of the bearing. Bearings are NOT drawn in standard position, which means the are NOT drawn from the positive x-axis.
Now we will will look at some application problems that involve bearings and right triangles.
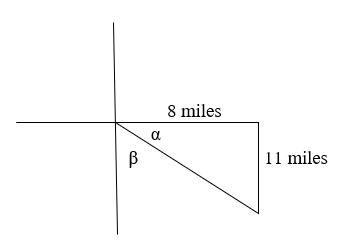
Example 9: Find the bearing
A semi travels east for 8 miles, makes a right turn, and then travels south for 11 more miles. What is the bearing from the starting point to the semi’s current location?
Try It
A cyclist travels west for 7 miles, makes a right turn and travels north for 4 miles. What is the bearing from the starting point to the cyclist’s current position? Round your angle to one decimal place.
Example 10: Find the bearing
A jeep travels on a bearing of [latex]N 40^\circ W[/latex] for 6 miles. How far north and how far west is the jeep from its starting point? Round your answers to one decimal place.
Try It
A jogger travels on a bearing of [latex]S 53.13^\circ E[/latex] for 5 miles. How far east and how far south is the jogger from their starting point? Round your answers to the nearest mile.
Convert Percent Grade Into Degrees
Percent grade is often seen on roadways or trails, and it is a measure of steepness. For example, if a road has a 6% grade, this means the road rises 6 feet over a horizontal distance (run) of 100 feet. Percent grade is found by dividing the rise over the run as shown in Figure 14. The rise and run are also the opposite and adjacent sides. We can find [latex]\theta[/latex] by taking the inverse tangent.

Figure 14
In order to calculate the degree measurement of a percent grade, first change the percent into a decimal by dividing by 100. Then take the inverse tangent of this decimal, and this will give the angle in degrees. This is actually the angle of elevation, which we studied earlier in this section!
How To: Convert Percent Grade inTo Degrees
Make sure your calculator is in degree mode. Given the percent grade, the angle [latex]\theta[/latex] can be calculated using:
[latex]\theta=\tan^{-1}\left(\dfrac{\text{percent grade}}{100}\right)[/latex]
Example 11: Percent Grade to Degrees
Filbert Street, the steepest street in San Francisco, has a 31.5% grade. What is the angle the street makes with a horizontal line, rounded to one decimal place?
Try It
A road has a grade of 10.9%. What is the angle the road makes with a horizontal line, rounded to one decimal place?
Key Equations
| Cofunction Identities | [latex]\begin{gathered} \cos t=\sin \left(\frac{\pi }{2}-t\right) \\ \sin t=\cos \left(\frac{\pi }{2}-t\right)\\ \tan t=\cot \left(\frac{\pi }{2}-t\right) \\ \cot t=\tan \left(\frac{\pi }{2}-t\right) \\ \sec t=\csc \left(\frac{\pi }{2}-t\right) \\ \csc t=\sec \left(\frac{\pi }{2}-t\right) \end{gathered}[/latex] |
| Percent Grade to Degrees | [latex]\theta=\tan^{-1}\left(\dfrac{\text{percent grade}}{100}\right)[/latex] |
Key Concepts
- We can define trigonometric functions as ratios of the side lengths of a right triangle.
- The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle.
- We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur.
- Any two complementary angles could be the two acute angles of a right triangle.
- If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa.
- We can use trigonometric functions of an angle to find unknown side lengths.
- Select the trigonometric function representing the ratio of the unknown side to the known side.
- Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
- The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known.
- Bearings are measured from either from N or S, depending on the first letter of the bearing.
- Percent grade can be expressed as a degree, which is the angle of elevation.
Glossary
- adjacent side
- in a right triangle, the side between a given angle and the right angle
- angle of depression
- the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned lower than the observer
- angle of elevation
- the angle between the horizontal and the line from the object to the observer’s eye, assuming the object is positioned higher than the observer
- opposite side
- in a right triangle, the side most distant from a given angle
- hypotenuse
- the side of a right triangle opposite the right angle
- percent grade
- The ratio of the rise over the run, expressed as a percent. It is a measure of steepness.
Section 4.3 Homework Exercises
1. For the given right triangle, label the adjacent side, opposite side, and hypotenuse for the indicated angle.
2. When a right triangle with a hypotenuse of 1 is placed in the unit circle, which sides of the triangle correspond to the x- and y-coordinates?
3. The tangent of an angle compares which sides of the right triangle?
4. What is the relationship between the two acute angles in a right triangle?
5. Explain the cofunction identity.
For the following exercises, evaluate the expression. Rationalize the denominator if necessary.
6. [latex]\sin\frac{\pi}{4}\cos\frac{\pi}{4}-\tan\frac{\pi}{3}[/latex]
7. [latex]\sin\frac{\pi}{4}\cos\frac{\pi}{3}-\tan\frac{\pi}{4}[/latex]
8. [latex]2\sec^{2}\frac{\pi}{4}+\cot^{2}\frac{\pi}{3}[/latex]
9. [latex]3\csc^{2}\frac{\pi}{3}+\cot^{2}\frac{\pi}{4}[/latex]
For the following exercises, use cofunctions of complementary angles.
10. [latex]\cos \left(34^\circ\right)=\sin \left(\text{__}^\circ\right)[/latex]
11. [latex]\cos \left(\frac{\pi }{3}\right)=\sin \text{(___)}[/latex]
12. [latex]\csc \left(21^\circ\right)=\sec \left(\text{___}^\circ \right)[/latex]
13. [latex]\tan \left(\frac{\pi }{4}\right)=\cot \left(\text{__}\right)[/latex]
For the following exercises, find the lengths of the missing sides if side [latex]a[/latex] is opposite angle [latex]A[/latex], side [latex]b[/latex] is opposite angle [latex]B[/latex], and side [latex]c[/latex] is the hypotenuse.
14. [latex]\cos B=\frac{4}{5},a=10[/latex]
15. [latex]\sin B=\frac{1}{2}, a=20[/latex]
16. [latex]\tan A=\frac{5}{12},b=6[/latex]
17. [latex]\tan A=100,b=100[/latex]
18. [latex]\sin B=\frac{1}{\sqrt{3}}, a=2[/latex]
19. [latex]a=5,\measuredangle A={60}^{\circ }[/latex]
20. [latex]c=12,\measuredangle A={45}^{\circ }[/latex]
For the following exercises, use Figure 14 to evaluate each trigonometric function of angle [latex]A[/latex].
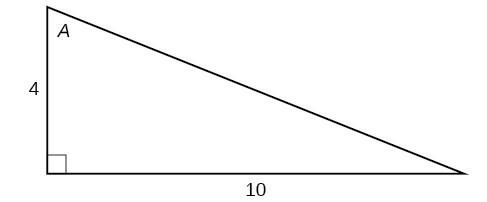
Figure 14
21. [latex]\sin A[/latex]
22. [latex]\cos A[/latex]
23. [latex]\tan A[/latex]
24. [latex]\csc A[/latex]
25. [latex]\sec A[/latex]
26. [latex]\cot A[/latex]
For the following exercises, use Figure 15 to evaluate each trigonometric function of angle [latex]A[/latex].
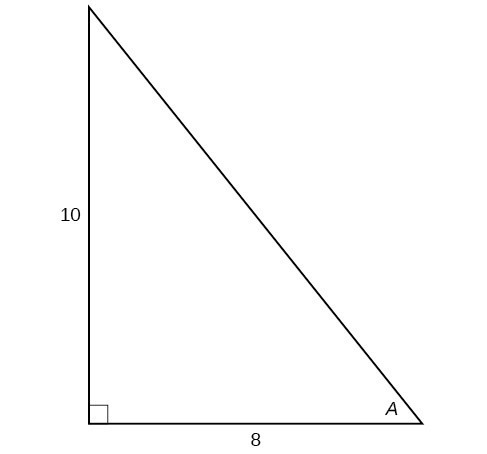
Figure 15
27. [latex]\sin A[/latex]
28. [latex]\cos A[/latex]
29. [latex]\tan A[/latex]
30. [latex]\csc A[/latex]
31. [latex]\sec A[/latex]
32. [latex]\cot A[/latex]
For the following exercises, solve for the unknown sides of the given triangle.
33.
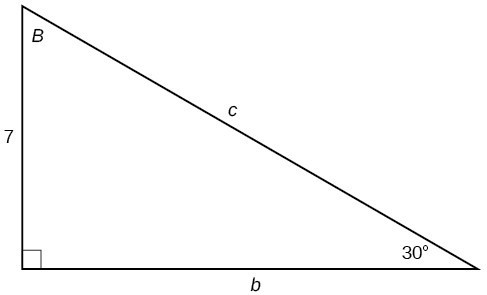
34.

35.

For the following exercises, use a calculator to find the length of each side to four decimal places.
36.
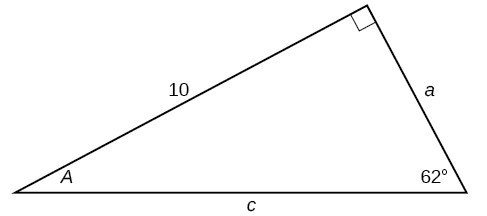
37.

38.

39.

40.

41. [latex]b=15,\measuredangle B={15}^{\circ }[/latex]
42. [latex]c=200,\measuredangle B={5}^{\circ }[/latex]
43. [latex]c=50,\measuredangle B={21}^{\circ }[/latex]
44. [latex]a=30,\measuredangle A={27}^{\circ }[/latex]
45. [latex]b=3.5,\measuredangle A={78}^{\circ }[/latex]
46. Find [latex]x[/latex].
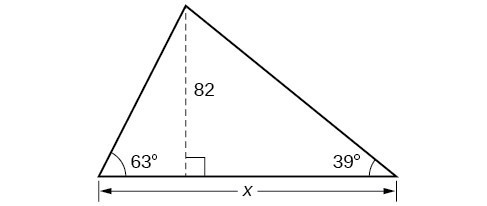
47. Find [latex]x[/latex].

48. Find [latex]x[/latex].

49. Find [latex]x[/latex].

50. A radio tower is located 400 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]36^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]23^\circ [/latex]. How tall is the tower?
51. A radio tower is located 325 feet from a building. From a window in the building, a person determines that the angle of elevation to the top of the tower is [latex]43^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]31^\circ [/latex]. How tall is the tower?
52. A 200-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]15^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]2^\circ [/latex]. How far is the person from the monument?
53. A 400-foot tall monument is located in the distance. From a window in a building, a person determines that the angle of elevation to the top of the monument is [latex]18^\circ [/latex], and that the angle of depression to the bottom of the tower is [latex]3^\circ [/latex]. How far is the person from the monument?
54. There is an antenna on the top of a building. From a location 300 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]40^\circ [/latex]. From the same location, the angle of elevation to the top of the antenna is measured to be [latex]43^\circ [/latex]. Find the height of the antenna.
55. There is lightning rod on the top of a building. From a location 500 feet from the base of the building, the angle of elevation to the top of the building is measured to be [latex]36^\circ [/latex]. From the same location, the angle of elevation to the top of the lightning rod is measured to be [latex]38^\circ [/latex]. Find the height of the lightning rod.
56. A 33-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ [/latex]. How high does the ladder reach up the side of the building?
57. A 23-ft ladder leans against a building so that the angle between the ground and the ladder is [latex]80^\circ [/latex]. How high does the ladder reach up the side of the building?
58. The angle of elevation to the top of a building in New York is found to be 9 degrees from the ground at a distance of 1 mile from the base of the building. Using this information, find the height of the building.
59. The angle of elevation to the top of a building in Seattle is found to be 2 degrees from the ground at a distance of 2 miles from the base of the building. Using this information, find the height of the building.
60. Assuming that a 370-foot tall giant redwood grows vertically, if I walk a certain distance from the tree and measure the angle of elevation to the top of the tree to be [latex]60^\circ [/latex], how far from the base of the tree am I?
61. A car travels west for 5 miles, turns left, and then travels south for 9 miles. What is the bearing from car’s starting position to its current position? Round your answer to two decimal places.
62. A truck travels east for 4 miles, turns left, and then travels north for 6 miles. What is the bearing from the truck’s starting position to its current position? Round your answer to two decimal places.
63. An ant travels on a bearing of [latex]N 22^\circ E[/latex] for 36 inches. How far east and how far north is the ant from its starting position? Round your answers to two decimal places.
64. A spider crawls on a bearing of [latex]S 34^\circ W[/latex] for 20 inches. How far west and how far south is the spider from its starting point? Round your answers to two decimal places.
65. Originally built in 1901 by Colonel J.W. Eddy, Angels Flight in Los Angeles is said to be the world’s shortest incorporated railway. The counterbalanced cars, controlled by cables, travel a 33% grade for 315 feet. What is the angle the track makes with a horizontal line, rounded to one decimal place?
66. The Saluda Grade is the steepest standard-gauge mainline railway grade in the United States. Between Melrose and Saluda, North Carolina, the maximum grade is 4.9% for about 300 feet. What is the angle the track makes with a horizontal line, rounded to one decimal place?