Learning Outcomes
- Model addition of integers with color counters
- Model integer subtraction with color counters
- Multiply integers with different signs
- Multiply integers with the same sign
- Multiply an integer by -1
- Divide integers with the same sign
- Divide integers with different signs
- Divide integers by -1
- Use correct notation to indicate absolute value
- Simplify expressions that contain absolute value
- Evaluate expressions that contain absolute value
- Use the order of operations to simplify expressions that involve integer multiplication, division, addition, and subtraction
- Evaluate integer expressions using the order of operations
Modeling Addition of Integers
We will first discuss arithmetic operations with integers.
Most students are comfortable with the addition and subtraction facts for positive numbers. But doing addition or subtraction with both positive and negative numbers may be more difficult. This difficulty relates to the way the brain learns.
The brain learns best by working with objects in the real world and then generalizing to abstract concepts. Toddlers learn quickly that if they have two cookies and their older brother steals one, they have only one left. This is a concrete example of [latex]2 - 1[/latex]. Children learn their basic addition and subtraction facts from experiences in their everyday lives. Eventually, they know the number facts without relying on cookies.
Addition and subtraction of negative numbers have fewer real world examples that are meaningful to us. Math teachers have several different approaches, such as number lines, banking, temperatures, and so on, to make these concepts real.
We will model addition and subtraction of negatives with two color counters. We let a blue counter represent a positive and a red counter will represent a negative.

If we have one positive and one negative counter, the value of the pair is zero. They form a neutral pair. The value of this neutral pair is zero as summarized in the figure below.
A blue counter represents [latex]+1[/latex]. A red counter represents [latex]-1[/latex]. Together they add to zero.

Doing the Manipulative Mathematics activity “Addition of signed Numbers” will help you develop a better understanding of adding integers.
We will model four addition facts using the numbers [latex]5,-5\text{ and }3,-3[/latex].
[latex]5+3 - 5+\left(-3\right)-5+35+\left(-3\right)[/latex]
example
Model: [latex]5+3[/latex].
Solution:
| Interpret the expression. | [latex]5+3[/latex] means the sum of [latex]5[/latex] and [latex]3[/latex] . |
| Model the first number. Start with [latex]5[/latex] positives. |  |
| Model the second number. Add [latex]3[/latex] positives. |  |
| Count the total number of counters. |  |
| The sum of [latex]5[/latex] and [latex]3[/latex] is [latex]8[/latex]. | [latex]5+3=8[/latex] |
try it
Model the expression.
[latex]2+4[/latex]
Model the expression.
[latex]2+5[/latex]
example
Model: [latex]-5+\left(-3\right)[/latex].
try it
Model the expression.
[latex]-2+\left(-4\right)[/latex]
Model the expression.
[latex]-2+\left(-5\right)[/latex]
The first and second examples are very similar. The first example adds [latex]5[/latex] positives and [latex]3[/latex] positives—both positives. The second example adds [latex]5[/latex] negatives and [latex]3[/latex] negatives—both negatives. In each case, we got a result of [latex]\text{8-either}8[/latex] positives or [latex]8[/latex] negatives. When the signs are the same, the counters are all the same color.
Now let’s see what happens when the signs are different.
example
Model: [latex]-5+3[/latex].
Notice that there were more negatives than positives, so the result is negative.
try it
Model the expression, and then simplify:
[latex]2+\left(-4\right)[/latex]
Model the expression, and then simplify:
[latex]2+\left(-5\right)[/latex]
example
Model: [latex]5+\left(-3\right)[/latex].
try it
Model the expression, and then simplify:
[latex]2+\left(-4\right)[/latex]
Model the expression:
[latex]\left(-2\right)+5[/latex]
example
Model each addition.
- [latex]4 + 2[/latex]
- [latex]−3 + 6[/latex]
- [latex]4 + (−5)[/latex]
- [latex]-2 + (−3)[/latex]
try it
Model each addition.
1. [latex]3 + 4[/latex]
2. [latex]−1 + 4[/latex]
3. [latex]4 + (−6)[/latex]
4. [latex]−2 + (−2)[/latex]
1. [latex]5 + 1[/latex]
2. [latex]−3 + 7[/latex]
3. [latex]2 + (−8)[/latex]
4. [latex]−3 + (−4)[/latex]
In the following video we present more examples of using color counters to model addition of integers.
Modeling Subtraction of Integers
You learn as a child how to subtract numbers through everyday experiences. For example, if you have 10 animal cookies and eat 6 of them, you will have 4 animal cookies left.
Real-life experiences serve as models for subtracting positive numbers, and in some cases, such as temperature, for adding negative as well as positive numbers. But it is difficult to relate subtracting negative numbers to common life experiences. Most people do not have an intuitive understanding of subtraction when negative numbers are involved. Math teachers use several different models to explain subtracting negative numbers.
We will continue to use counters to model subtraction. Remember, the blue counters represent positive numbers and the red counters represent negative numbers.
Perhaps when you were younger, you read [latex]5 - 3[/latex] as five take away three. When we use counters, we can think of subtraction the same way.
We will model four subtraction scenarios using the numbers [latex]5[/latex] and [latex]3[/latex].
- [latex]5 - 3[/latex]
- [latex]- 5-\left(-3\right)[/latex]
- [latex]-5 - 3[/latex]
- [latex]5-\left(-3\right)[/latex]
example
Model: [latex]5 - 3[/latex].
Solution:
| Interpret the expression. | [latex]5 - 3[/latex] means [latex]5[/latex] take away [latex]3[/latex] . |
| Model the first number. Start with [latex]5[/latex] positives. |  |
| Take away the second number. So take away [latex]3[/latex] positives. |  |
| Find the counters that are left. |  |
| [latex]5 - 3=2[/latex] .
The difference between [latex]5[/latex] and [latex]3[/latex] is [latex]2[/latex] . |
Now you can try a similar problem.
try it
Model the expression:
[latex]6 - 4[/latex]
Model the expression:
[latex]7 - 4[/latex]
In teh previous example we subtracted [latex]3[/latex] positives from positive [latex]5[/latex]. Now we will subtract [latex]3[/latex] negatives from negative [latex]5[/latex]. Compare the results of this example to the previous example after you read through it.
example
Model: [latex]-5-\left(-3\right)[/latex]
You can try a similar problem.
try it
Model the expression:
[latex]-6-\left(-4\right)[/latex]
Model the expression:
[latex]-7-\left(-4\right)[/latex]
Notice that the previous two examples are very much alike.
- First, we subtracted [latex]3[/latex] positives from [latex]5[/latex] positives to get [latex]2[/latex] positives.
- Then we subtracted [latex]3[/latex] negatives from [latex]5[/latex] negatives to get [latex]2[/latex] negatives.
Each example used counters of only one color, and the “take away” model of subtraction was easy to apply.
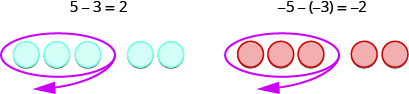
Now let’s see what happens when we subtract one positive and one negative number. We will need to use both positive and negative counters and sometimes some neutral pairs, too. Adding a neutral pair does not change the value.
example
Model: [latex]-5 - 3[/latex].
Now you can try a similar problem.
try it
Model the expression:
[latex]-6 - 4[/latex]
Model the expression:
[latex]-7 - 4[/latex]
Now we will subtract a negative number from a positive number. Think of this as taking away the negative.
example
Model: [latex]5-\left(-3\right)[/latex].
Now you can try a similar problem.
try it
Model the expression:
[latex]6-\left(-4\right)[/latex]
Model the expression:
[latex]7-\left(-4\right)[/latex]
Now we will do an example that summarizes the situations above, with different numbers. Recall the different scenarios:
- subtracting a positive number from a positive number
- subtracting a positive number from a negative number
- subtracting a negative number from a positive number
- subtracting a negative number from a negative number
example
Model each subtraction.
[latex]8 − 2[/latex]
[latex]−5 − 4[/latex]
[latex]6 − (−6)[/latex]
[latex]−8 − (−3)[/latex]
Now you can try a similar problem.
try it
Model each subtraction.
1. [latex]7 - (-8)[/latex]
2. [latex]-7 - (-2)[/latex]
3. [latex]4 - 1[/latex]
4. [latex]-6 - 8[/latex]
Model each subtraction.
1. [latex]4 - (-6)[/latex]
2. [latex]-8 - (-1)[/latex]
3. [latex]7 - 3[/latex]
4. [latex]-4 - 2[/latex]
Each of the examples so far have been carefully constructed so that the sign of the answer matched the sign of the first number in the expression. For example, in [latex]−5 − 4[/latex], the result is [latex]-9[/latex], which is the same sign as [latex]-5[/latex]. Now we will see subtraction where the sign of the result is different from the starting number.
example
Model each subtraction expression:
- [latex]2 - 8[/latex]
- [latex]-3-\left(-8\right)[/latex]
Now you can try a similar problem.
try it
Model each subtraction expression.
- [latex]7 - 9[/latex]
- [latex]-5-(-9)[/latex]
Model each subtraction expression.
- [latex]4 - 7[/latex]
- [latex]-7-\left(-10\right)[/latex]
When you subtract two integers, there are two possibilities, either the result will have a different sign from the starting number, or it will have the same sign.
Watch the video below to see more examples of modeling integer subtraction with color counters.
Modeling Multiplication of Integers
Since multiplication is mathematical shorthand for repeated addition, our counter model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction.
We remember that [latex]a\cdot b[/latex] means add [latex]a,b[/latex] times. Here, we are using the model shown in the graphic below just to help us discover the pattern.

Now consider what it means to multiply [latex]5[/latex] by [latex]-3[/latex]. It means subtract [latex]5,3[/latex] times. Looking at subtraction as taking away, it means to take away [latex]5,3[/latex] times. But there is nothing to take away, so we start by adding neutral pairs as shown in the graphic below.

In both cases, we started with [latex]\mathbf{\text{15}}[/latex] neutral pairs. In the case on the left, we took away [latex]\mathbf{\text{5}},\mathbf{\text{3}}[/latex] times and the result was [latex]-\mathbf{\text{15}}[/latex]. To multiply [latex]\left(-5\right)\left(-3\right)[/latex], we took away [latex]-\mathbf{\text{5}},\mathbf{\text{3}}[/latex] times and the result was [latex]\mathbf{\text{15}}[/latex]. So we found that
[latex]\begin{array}{ccc}5\cdot 3=15\hfill & & -5\left(3\right)=-15\hfill \\ 5\left(-3\right)=-15\hfill & & \left(-5\right)\left(-3\right)=15\hfill \end{array}[/latex]
Notice that for multiplication of two signed numbers, when the signs are the same, the product is positive, and when the signs are different, the product is negative.
Multiplication of Signed Numbers
The sign of the product of two numbers depends on their signs.
| Same signs | Product |
|---|---|
| •Two positives
•Two negatives |
Positive
Positive |
| Different signs | Product |
|---|---|
| •Positive • negative
•Negative • positive |
Negative
Negative |
example
Multiply each of the following:
- [latex]-9\cdot 3[/latex]
- [latex]-2\left(-5\right)[/latex]
- [latex]4\left(-8\right)[/latex]
- [latex]7\cdot 6[/latex]
Solution:
| 1. | |
| [latex]-9\cdot 3[/latex] | |
| Multiply, noting that the signs are different and so the product is negative. | [latex]-27[/latex] |
| 2. | |
| [latex]-2\left(-5\right)[/latex] | |
| Multiply, noting that the signs are the same and so the product is positive. | [latex]10[/latex] |
| 3. | |
| [latex]4\left(-8\right)[/latex] | |
| Multiply, noting that the signs are different and so the product is negative. | [latex]-32[/latex] |
| 4. | |
| [latex]7\cdot 6[/latex] | |
| The signs are the same, so the product is positive. | [latex]42[/latex] |
try it
Watch the following video for more examples of how to multiply integers with different signs, and the same sign.
When we multiply a number by [latex]1[/latex], the result is the same number. What happens when we multiply a number by [latex]-1?[/latex] Let’s multiply a positive number and then a negative number by [latex]-1[/latex] to see what we get.
[latex]\begin{array}{ccc}\hfill -1\cdot 4\hfill & & \hfill -1\left(-3\right)\hfill \\ \hfill -4\hfill & & \hfill 3\hfill \\ \hfill -4\text{ is the opposite of }\mathbf{\text{4}}\hfill & & \hfill \mathbf{\text{3}}\text{ is the opposite of }-3\hfill \end{array}[/latex]
Each time we multiply a number by [latex]-1[/latex], we get its opposite.
Multiplication by [latex]-1[/latex]
Multiplying a number by [latex]-1[/latex] gives its opposite.
[latex]-1a=-a[/latex]
example
Multiply each of the following:
- [latex]-1\cdot 7[/latex]
- [latex]-1\left(-11\right)[/latex]
try it
Division with Integers
Division is the inverse operation of multiplication. So, [latex]15\div 3=5[/latex] because [latex]5\cdot 3=15[/latex] In words, this expression says that [latex]\mathbf{\text{15}}[/latex] can be divided into [latex]\mathbf{\text{3}}[/latex] groups of [latex]\mathbf{\text{5}}[/latex] each because adding five three times gives [latex]\mathbf{\text{15}}[/latex]. If we look at some examples of multiplying integers, we might figure out the rules for dividing integers.
[latex]\begin{array}{ccccc}5\cdot 3=15\text{ so }15\div 3=5\hfill & & & & -5\left(3\right)=-15\text{ so }-15\div 3=-5\hfill \\ \left(-5\right)\left(-3\right)=15\text{ so }15\div \left(-3\right)=-5\hfill & & & & 5\left(-3\right)=-15\text{ so }-15\div -3=5\hfill \end{array}[/latex]
Division of signed numbers follows the same rules as multiplication. When the signs are the same, the quotient is positive, and when the signs are different, the quotient is negative.
Division of Signed Numbers
The sign of the quotient of two numbers depends on their signs.
| Same signs | Quotient |
|---|---|
| •Two positives
•Two negatives |
Positive
Positive |
| Different signs | Quotient |
|---|---|
| •Positive & negative
•Negative & positive |
Negative
Negative |
Remember, you can always check the answer to a division problem by multiplying.
example
Divide each of the following:
- [latex]-27\div 3[/latex]
- [latex]-100\div \left(-4\right)[/latex]
Solution
| 1. | |
| [latex]-27\div 3[/latex] | |
| Divide, noting that the signs are different and so the quotient is negative. | [latex]-9[/latex] |
| 2. | |
| [latex]-100\div \left(-4\right)[/latex] | |
| Divide, noting that the signs are the same and so the quotient is positive. | [latex]25[/latex] |
try it
Just as we saw with multiplication, when we divide a number by [latex]1[/latex], the result is the same number. What happens when we divide a number by [latex]-1?[/latex] Let’s divide a positive number and then a negative number by [latex]-1[/latex] to see what we get.
[latex]\begin{array}{cccc}8\div \left(-1\right)\hfill & & & -9\div \left(-1\right)\hfill \\ -8\hfill & & & 9\hfill \\ \hfill \text{-8 is the opposite of 8}\hfill & & & \hfill \text{9 is the opposite of -9}\hfill \end{array}[/latex]
When we divide a number by [latex]-1[/latex] we get its opposite.
Division by [latex]-1[/latex]
Dividing a number by [latex]-1[/latex] gives its opposite.
[latex]a\div \left(-1\right)=-a[/latex]
example
Divide each of the following:
- [latex]16\div \left(-1\right)[/latex]
- [latex]-20\div \left(-1\right)[/latex]
try it
Watch the following video for more examples of how to divide integers with the same and different signs.
Absolute Value
We saw that numbers such as [latex]5[/latex] and [latex]-5[/latex] are opposites because they are the same distance from [latex]0[/latex] on the number line. They are both five units from [latex]0[/latex]. The distance between [latex]0[/latex] and any number on the number line is called the absolute value of that number. Because distance is never negative, the absolute value of any number is never negative.
The symbol for absolute value is two vertical lines on either side of a number. So the absolute value of [latex]5[/latex] is written as [latex]|5|[/latex], and the absolute value of [latex]-5[/latex] is written as [latex]|-5|[/latex] as shown below.

Absolute Value
The absolute value of a number is its distance from [latex]0[/latex] on the number line.
The absolute value of a number [latex]n[/latex] is written as [latex]|n|[/latex].
[latex]|n|\ge 0\text{ for all numbers}[/latex]
example
Simplify:
[latex]|3|[/latex]
[latex]|-44|[/latex]
[latex]|0|[/latex]
Solution:
| 1. | |
| [latex]|3|[/latex] | |
| [latex]3[/latex] is [latex]3[/latex] units from zero. | [latex]3[/latex] |
| 2. | |
| [latex]|-44|[/latex] | |
| [latex]−44[/latex] is [latex]44[/latex] units from zero. | [latex]44[/latex] |
| 3. | |
| [latex]|0|[/latex] | |
| [latex]0[/latex] is already at zero. | [latex]0[/latex] |
try it
In the video below we show more example of how to find the absolute value of an integer.
We treat absolute value bars just like we treat parentheses in the order of operations. We simplify the expression inside first.
example
Evaluate:
- [latex]|x|\text{ when }x=-35[/latex]
- [latex]|\mathit{\text{-y}}|\text{ when }y=-20[/latex]
- [latex]-|u|\text{ when }u=12[/latex]
- [latex]-|p|\text{ when }p=-14[/latex]
Notice that the result is negative only when there is a negative sign outside the absolute value symbol.
try it
example
Fill in [latex]\text{<},\text{>},\text{or}=[/latex] for each of the following:
- [latex]|-5|___-|-5|[/latex]
- [latex]8___-|-8|[/latex]
- [latex]-9___-|-9|[/latex]
- [latex]-|-7|___ - 7[/latex]
try it
In the video below we show more examples of how to compare expressions that include absolute value and integers.
Absolute value bars act like grouping symbols. First simplify inside the absolute value bars as much as possible. Then take the absolute value of the resulting number, and continue with any operations outside the absolute value symbols.
example
Simplify:
- [latex]|9 - 3|[/latex]
- [latex]4|-2|[/latex]
try it
example
Simplify: [latex]|8+7|-|5+6|[/latex].
try it
example
Simplify: [latex]24-|19 - 3\left(6 - 2\right)|[/latex].
try it
Watch the following video to see more examples of how to simplify expressions that contain absolute value.
Simplify Expressions Using the Order of Operations
We’ve introduced most of the symbols and notation used in algebra, but now we need to clarify the order of operations. Otherwise, expressions may have different meanings, and they may result in different values.
For example, consider the expression:
[latex]4+3\cdot 7[/latex]
[latex]\begin{array}{cccc}\hfill \text{Some students say it simplifies to 49.}\hfill & & & \hfill \text{Some students say it simplifies to 25.}\hfill \\ \begin{array}{ccc}& & \hfill 4+3\cdot 7\hfill \\ \text{Since }4+3\text{ gives 7.}\hfill & & \hfill 7\cdot 7\hfill \\ \text{And }7\cdot 7\text{ is 49.}\hfill & & \hfill 49\hfill \end{array}& & & \begin{array}{ccc}& & \hfill 4+3\cdot 7\hfill \\ \text{Since }3\cdot 7\text{ is 21.}\hfill & & \hfill 4+21\hfill \\ \text{And }21+4\text{ makes 25.}\hfill & & \hfill 25\hfill \end{array}\hfill \end{array}[/latex]
Imagine the confusion that could result if every problem had several different correct answers. The same expression should give the same result. So mathematicians established some guidelines called the order of operations, which outlines the order in which parts of an expression must be simplified.
Order of Operations
When simplifying mathematical expressions perform the operations in the following order:
1. Parentheses and other Grouping Symbols
- Simplify all expressions inside the parentheses or other grouping symbols, working on the innermost parentheses first.
2. Exponents
- Simplify all expressions with exponents.
3. Multiplication and Division
- Perform all multiplication and division in order from left to right. These operations have equal priority.
4. Addition and Subtraction
- Perform all addition and subtraction in order from left to right. These operations have equal priority.
Students often ask, “How will I remember the order?” Here is a way to help you remember: Take the first letter of each key word and substitute the silly phrase. Please Excuse My Dear Aunt Sally.
| Order of Operations | |
|---|---|
| Please | Parentheses |
| Excuse | Exponents |
| My Dear | Multiplication and Division |
| Aunt Sally | Addition and Subtraction |
It’s good that ‘My Dear’ goes together, as this reminds us that multiplication and division have equal priority. We do not always do multiplication before division or always do division before multiplication. We do them in order from left to right.
Similarly, ‘Aunt Sally’ goes together and so reminds us that addition and subtraction also have equal priority and we do them in order from left to right.
example
Simplify the expressions:
- [latex]4+3\cdot 7[/latex]
- [latex]\left(4+3\right)\cdot 7[/latex]
Solution:
| 1. | |
| [latex]4+3\cdot 7[/latex] | |
| Are there any parentheses? No. | |
| Are there any exponents? No. | |
| Is there any multiplication or division? Yes. | |
| Multiply first. | [latex]4+\color{red}{3\cdot 7}[/latex] |
| Add. | [latex]4+21[/latex] |
| [latex]25[/latex] |
| 2. | |
| [latex](4+3)\cdot 7[/latex] | |
| Are there any parentheses? Yes. | [latex]\color{red}{(4+3)}\cdot 7[/latex] |
| Simplify inside the parentheses. | [latex](7)7[/latex] |
| Are there any exponents? No. | |
| Is there any multiplication or division? Yes. | |
| Multiply. | [latex]49[/latex] |
try it
example
Simplify:
- [latex]\text{18}\div \text{9}\cdot \text{2}[/latex]
- [latex]\text{18}\cdot \text{9}\div \text{2}[/latex]
try it
example
Simplify: [latex]18\div 6+4\left(5 - 2\right)[/latex].
try it
In the video below we show another example of how to use the order of operations to simplify a mathematical expression.
When there are multiple grouping symbols, we simplify the innermost parentheses first and work outward.
example
[latex]\text{Simplify: }5+{2}^{3}+3\left[6 - 3\left(4 - 2\right)\right][/latex].
try it
In the video below we show another example of how to use the order of operations to simplify an expression that contains exponents and grouping symbols.
example
Simplify: [latex]{2}^{3}+{3}^{4}\div 3-{5}^{2}[/latex].
try it
example
[latex]\text{Simplify: }7\left(-2\right)+4\left(-7\right)-6[/latex].
Solution:
We use the order of operations. Multiply first and then add and subtract from left to right.
| [latex]7\left(-2\right)+4\left(-7\right)-6[/latex] | |
| Multiply first. | [latex]-14+\left(-28\right)-6[/latex] |
| Add. | [latex]-42 - 6[/latex] |
| Subtract. | [latex]-48[/latex] |
try it
Watch the following video to see another example of how to use the order of operations to simplify an expression that contains integers.
In our next example we will simplify expressions with integers that also contain exponents.
example
Simplify:
1.
[latex]{\left(-2\right)}^{4}[/latex]
2.
[latex]{-2}^{4}[/latex]
Now you try it.
try it
In the following example we provide an explanation for the difference between [latex](-3)^2[/latex] and [latex]-3^2[/latex].
example
[latex]\text{Simplify: }12 - 3\left(9 - 12\right)[/latex].
try it
example
Simplify: [latex]8\left(-9\right)\div {\left(-2\right)}^{3}[/latex].
try it
example
[latex]\text{Simplify:}-30\div 2+\left(-3\right)\left(-7\right)[/latex].
try it
In the following video we show more examples of how to evaluate expressions with integers using the order of operations.



























































































