Learning Outcomes
- Use variables to represent unknown quantities in algebraic expressions
- Identify the variables and constants in an algebraic expression
- Use words and symbols to represent algebraic operations on variables and constants
- Simplify expressions with exponents containing integer bases and variable bases
- Evaluate an expression for a given value
- Identify the variables and constants in a term
- Identify the coefficient of a variable term
- Identify and combine like terms in an expression
- Apply the distributive property to simplify an algebraic expression
Use Variables and Algebraic Symbols
Greg and Alex have the same birthday, but they were born in different years. This year Greg is [latex]20[/latex] years old and Alex is [latex]23[/latex], so Alex is [latex]3[/latex] years older than Greg. When Greg was [latex]12[/latex], Alex was [latex]15[/latex]. When Greg is [latex]35[/latex], Alex will be [latex]38[/latex]. No matter what Greg’s age is, Alex’s age will always be [latex]3[/latex] years more, right?
In the language of algebra, we say that Greg’s age and Alex’s age are variable and the three is a constant. The ages change, or vary, so age is a variable. The [latex]3[/latex] years between them always stays the same, so the age difference is the constant.
In algebra, letters of the alphabet are used to represent variables. Suppose we call Greg’s age [latex]g[/latex]. Then we could use [latex]g+3[/latex] to represent Alex’s age. See the table below.
| Greg’s age | Alex’s age |
|---|---|
| [latex]12[/latex] | [latex]15[/latex] |
| [latex]20[/latex] | [latex]23[/latex] |
| [latex]35[/latex] | [latex]38[/latex] |
| [latex]g[/latex] | [latex]g+3[/latex] |
Letters are used to represent variables. Letters often used for variables are [latex]x,y,a,b,\text{ and }c[/latex].
Variables and Constants
A variable is a letter that represents a number or quantity whose value may change.
A constant is a number whose value always stays the same.
To write algebraically, we need some symbols as well as numbers and variables. There are several types of symbols we will be using. In Whole Numbers, we introduced the symbols for the four basic arithmetic operations: addition, subtraction, multiplication, and division. We will summarize them here, along with words we use for the operations and the result.
| Operation | Notation | Say: | The result is… |
|---|---|---|---|
| Addition | [latex]a+b[/latex] | [latex]a\text{ plus }b[/latex] | the sum of [latex]a[/latex] and [latex]b[/latex] |
| Subtraction | [latex]a-b[/latex] | [latex]a\text{ minus }b[/latex] | the difference of [latex]a[/latex] and [latex]b[/latex] |
| Multiplication | [latex]a\cdot b,\left(a\right)\left(b\right),\left(a\right)b,a\left(b\right)[/latex] | [latex]a\text{ times }b[/latex] | The product of [latex]a[/latex] and [latex]b[/latex] |
| Division | [latex]a\div b,a/b,\frac{a}{b},b\overline{)a}[/latex] | [latex]a[/latex] divided by [latex]b[/latex] | The quotient of [latex]a[/latex] and [latex]b[/latex] |
In algebra, the cross symbol, [latex]\times[/latex], is not used to show multiplication because that symbol may cause confusion. Does [latex]3xy[/latex] mean [latex]3\times y[/latex] (three times [latex]y[/latex] ) or [latex]3\cdot x\cdot y[/latex] (three times [latex]x\text{ times }y[/latex] )? To make it clear, use • or parentheses for multiplication.
We perform these operations on two numbers. When translating from symbolic form to words, or from words to symbolic form, pay attention to the words of or and to help you find the numbers.
- The sum of [latex]5[/latex] and [latex]3[/latex] means add [latex]5[/latex] plus [latex]3[/latex], which we write as [latex]5+3[/latex].
- The difference of [latex]9[/latex] and [latex]2[/latex] means subtract [latex]9[/latex] minus [latex]2[/latex], which we write as [latex]9 - 2[/latex].
- The product of [latex]4[/latex] and [latex]8[/latex] means multiply [latex]4[/latex] times [latex]8[/latex], which we can write as [latex]4\cdot 8[/latex].
- The quotient of [latex]20[/latex] and [latex]5[/latex] means divide [latex]20[/latex] by [latex]5[/latex], which we can write as [latex]20\div 5[/latex].
Exercises
Translate from algebra to words:
- [latex]12+14[/latex]
- [latex]\left(30\right)\left(5\right)[/latex]
- [latex]64\div 8[/latex]
- [latex]x-y[/latex]
Solution:
| 1. |
| [latex]12+14[/latex] |
| [latex]12[/latex] plus [latex]14[/latex] |
| the sum of twelve and fourteen |
| 2. |
| [latex]\left(30\right)\left(5\right)[/latex] |
| [latex]30[/latex] times [latex]5[/latex] |
| the product of thirty and five |
| 3. |
| [latex]64\div 8[/latex] |
| [latex]64[/latex] divided by [latex]8[/latex] |
| the quotient of sixty-four and eight |
| 4. |
| [latex]x-y[/latex] |
| [latex]x[/latex] minus [latex]y[/latex] |
| the difference of [latex]x[/latex] and [latex]y[/latex] |
TRY IT
Exponents
Remember that an exponent indicates repeated multiplication of the same quantity. For example, [latex]{2}^{4}[/latex] means to multiply four factors of [latex]2[/latex], so [latex]{2}^{4}[/latex] means [latex]2\cdot 2\cdot 2\cdot 2[/latex]. This format is known as exponential notation.
Exponential Notation
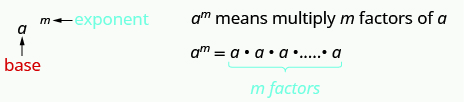
This is read [latex]a[/latex] to the [latex]{m}^{\mathrm{th}}[/latex] power.
In the expression [latex]{a}^{m}[/latex], the exponent tells us how many times we use the base [latex]a[/latex] as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
example
Simplify:
1. [latex]{5}^{3}[/latex]
2. [latex]{9}^{1}[/latex]
Solution
| 1. | |
| [latex]{5}^{3}[/latex] | |
| Multiply [latex]3[/latex] factors of [latex]5[/latex]. | [latex]5\cdot 5\cdot 5[/latex] |
| Simplify. | [latex]125[/latex] |
| 2. | |
| [latex]{9}^{1}[/latex] | |
| Multiply [latex]1[/latex] factor of [latex]9[/latex]. | [latex]9[/latex] |
try it
example
Simplify:
1. [latex]{\left(-3\right)}^{4}[/latex]
2. [latex]{-3}^{4}[/latex]
try it
example
Rewrite the following without exponents: [latex]-8a^{5}b[/latex].
Try it
Rewrite the following without exponents: [latex]11r^{4}s^{3}[/latex].
Evaluate Algebraic Expressions
To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
example
Evaluate [latex]x+7[/latex] when
- [latex]x=3[/latex]
- [latex]x=12[/latex]
Solution:
1. To evaluate, substitute [latex]3[/latex] for [latex]x[/latex] in the expression, and then simplify.
| [latex]x+7[/latex] | |
| Substitute. | [latex]\color{red}{3}+7[/latex] |
| Add. | [latex]10[/latex] |
When [latex]x=3[/latex], the expression [latex]x+7[/latex] has a value of [latex]10[/latex].
2. To evaluate, substitute [latex]12[/latex] for [latex]x[/latex] in the expression, and then simplify.
| [latex]x+7[/latex] | |
| Substitute. | [latex]\color{red}{12}+7[/latex] |
| Add. | [latex]19[/latex] |
When [latex]x=12[/latex], the expression [latex]x+7[/latex] has a value of [latex]19[/latex].
Notice that we got different results for parts 1 and 2 even though we started with the same expression. This is because the values used for [latex]x[/latex] were different. When we evaluate an expression, the value varies depending on the value used for the variable.
try it
example
Evaluate [latex]9x - 2,[/latex] when
- [latex]x=5[/latex]
- [latex]x=1[/latex]
example
Evaluate [latex]\frac{n}{d},[/latex] when [latex]n=35[/latex] and [latex]d=7[/latex].
try it
example
Evaluate [latex]{x}^{2}[/latex] when [latex]x=10[/latex].
try it
example
[latex]\text{Evaluate }{2}^{x}\text{ when }x=5[/latex].
try it
example
[latex]\text{Evaluate }3x+4y - 6\text{ when }x=10\text{ and }y=2[/latex].
TRY IT
example
[latex]\text{Evaluate }2{x}^{2}+3x+8\text{ when }x=4[/latex].
try it
In the video below we show more examples of how to substitute a value for variable in an expression, then evaluate the expression.
Identify Terms, Coefficients, and Like Terms
Algebraic expressions are made up of terms. A term is a constant or the product of a constant and one or more variables. Some examples of terms are [latex]7,y,5{x}^{2},9a,\text{and }13xy[/latex].
The constant that multiplies the variable(s) in a term is called the coefficient. We can think of the coefficient as the number in front of the variable. The coefficient of the term [latex]3x[/latex] is [latex]3[/latex]. When we write [latex]x[/latex], the coefficient is [latex]1[/latex], since [latex]x=1\cdot x[/latex]. The table below gives the coefficients for each of the terms in the left column.
| Term | Coefficient |
|---|---|
| [latex]7[/latex] | [latex]7[/latex] |
| [latex]9a[/latex] | [latex]9[/latex] |
| [latex]y[/latex] | [latex]1[/latex] |
| [latex]5{x}^{2}[/latex] | [latex]5[/latex] |
An algebraic expression may consist of one or more terms added or subtracted. In this chapter, we will only work with terms that are added together. The table below gives some examples of algebraic expressions with various numbers of terms. Notice that we include the operation before a term with it.
| Expression | Terms |
|---|---|
| [latex]7[/latex] | [latex]7[/latex] |
| [latex]y[/latex] | [latex]y[/latex] |
| [latex]x+7[/latex] | [latex]x,7[/latex] |
| [latex]2x+7y+4[/latex] | [latex]2x,7y,4[/latex] |
| [latex]3{x}^{2}+4{x}^{2}+5y+3[/latex] | [latex]3{x}^{2},4{x}^{2},5y,3[/latex] |
example
Identify each term in the expression [latex]9b+15{x}^{2}+a+6[/latex]. Then identify the coefficient of each term.
Solution:
The expression has four terms. They are [latex]9b,15{x}^{2},a[/latex], and [latex]6[/latex].
- The coefficient of [latex]9b[/latex] is [latex]9[/latex].
- The coefficient of [latex]15{x}^{2}[/latex] is [latex]15[/latex].
- Remember that if no number is written before a variable, the coefficient is [latex]1[/latex]. So the coefficient of [latex]a[/latex] is [latex]1[/latex].
- The coefficient of a constant is the constant, so the coefficient of [latex]6[/latex] is [latex]6[/latex].
try it
Some terms share common traits. Look at the following terms. Which ones seem to have traits in common?
[latex]5x,7,{n}^{2},4,3x,9{n}^{2}[/latex]
Which of these terms are like terms?
- The terms [latex]7[/latex] and [latex]4[/latex] are both constant terms.
- The terms [latex]5x[/latex] and [latex]3x[/latex] are both terms with [latex]x[/latex].
- The terms [latex]{n}^{2}[/latex] and [latex]9{n}^{2}[/latex] both have [latex]{n}^{2}[/latex].
Terms are called like terms if they have the same variables and exponents. All constant terms are also like terms. So among the terms [latex]5x,7,{n}^{2},4,3x,9{n}^{2}[/latex],
- [latex]7[/latex] and [latex]4[/latex] are like terms.
- [latex]5x[/latex] and [latex]3x[/latex] are like terms.
- [latex]{n}^{2}[/latex] and [latex]9{n}^{2}[/latex] are like terms.
Like Terms
Terms that are either constants or have the same variables with the same exponents are like terms.
example
Identify the like terms:
- [latex]{y}^{3},7{x}^{2},14,23,4{y}^{3},9x,5{x}^{2}[/latex]
- [latex]4{x}^{2}+2x+5{x}^{2}+6x+40x+8xy[/latex]
try it
Simplify Expressions by Combining Like Terms
We can simplify an expression by combining the like terms. What do you think [latex]3x+6x[/latex] would simplify to? If you thought [latex]9x[/latex], you would be right!
We can see why this works by writing both terms as addition problems.

Add the coefficients and keep the same variable. It doesn’t matter what [latex]x[/latex] is. If you have [latex]3[/latex] of something and add [latex]6[/latex] more of the same thing, the result is [latex]9[/latex] of them. For example, [latex]3[/latex] oranges plus [latex]6[/latex] oranges is [latex]9[/latex] oranges. We will discuss the mathematical properties behind this later.
The expression [latex]3x+6x[/latex] has only two terms. When an expression contains more terms, it may be helpful to rearrange the terms so that like terms are together. The Commutative Property of Addition says that we can change the order of addends without changing the sum. So we could rearrange the following expression before combining like terms.

Now it is easier to see the like terms to be combined.
Combine like terms
- Identify like terms.
- Rearrange the expression so like terms are together.
- Add the coefficients of the like terms.
example
Simplify the expression: [latex]3x+7+4x+5[/latex].
try it
example
Simplify the expression: [latex]8x+7{x}^{2}-{x}^{2}-+4x[/latex].
try it
In the following video, we present more examples of how to combine like terms given an algebraic expression.
Simplify Expressions Using the Distributive Property
Distributive Property
If [latex]a,b,c[/latex] are real numbers, then
[latex]a\left(b+c\right)=ab+ac[/latex]
In algebra, we use the Distributive Property to remove parentheses as we simplify expressions. For example, if we are asked to simplify the expression [latex]3\left(x+4\right)[/latex], the order of operations says to work in the parentheses first. But we cannot add [latex]x[/latex] and [latex]4[/latex], since they are not like terms. So we use the Distributive Property, as shown in the next example.
example
Simplify: [latex]3\left(x+4\right)[/latex]
Solution:
| [latex]3\left(x+4\right)[/latex] | |
| Distribute. | [latex]3\cdot x+3\cdot 4[/latex] |
| Multiply. | [latex]3x+12[/latex] |
Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the previous example would look like this:
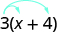
[latex]3\cdot x+3\cdot 4[/latex]
Now you try.
try it
In our next example, there is a coefficient on the variable y. When you use the distributive property, you multiply the two numbers together, just like simplifying any product. You will also see another example where the expression in parentheses is subtraction, rather than addition. You will need to be careful to change the sign of your product.
example
Simplify: [latex]6\left(5y+1\right)[/latex].
Simplify: [latex]2\left(x - 3\right)[/latex]
Now you try.
try it
The distributive property can be used to simplify expressions that look slightly different from [latex]a\left(b+c\right)[/latex]. Here are two other forms.
different Forms of the Distributive Property
If [latex]a,b,c[/latex] are real numbers, then
[latex]a\left(b+c\right)=ab+ac[/latex]
Other forms
[latex]a\left(b-c\right)=ab-ac[/latex]
[latex]\left(b+c\right)a=ba+ca[/latex]
In teh following video we show more examples of using the distributive property.


