Learning Outcomes
- Identify solutions of systems of equations
- Solve systems of equations by graphing
- Use the substitution method to find solution(s) to a system of two linear equations.
- Use the addition method to find solution(s) to a system of linear equations.
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time. Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
In this section, we will look at systems of linear equations in two variables which consist of two equations that each contain two different variables. For example, consider the following system of linear equations in two variables.
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly, we will investigate methods of finding such a solution if it exists.
In addition to considering the number of equations and variables, we can categorize systems of linear equations by the number of solutions. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution like the example we just explored. The two lines have different slopes and intersect at one point in the plane. A consistent system is considered to be a dependent system if the equations have the same slope and the same y-intercepts. In other words, the lines coincide, so the equations represent the same line. Every point on the line represents a coordinate pair that satisfies the system. Thus, there are an infinite number of solutions.
Another type of system of linear equations is an inconsistent system which is one where the equations represent two parallel lines. The lines have the same slope and different y-intercepts. There are no points common to both lines; hence, there is no solution to the system.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables and three types of solutions.
- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution.The two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
Below are graphical representations of each type of system.
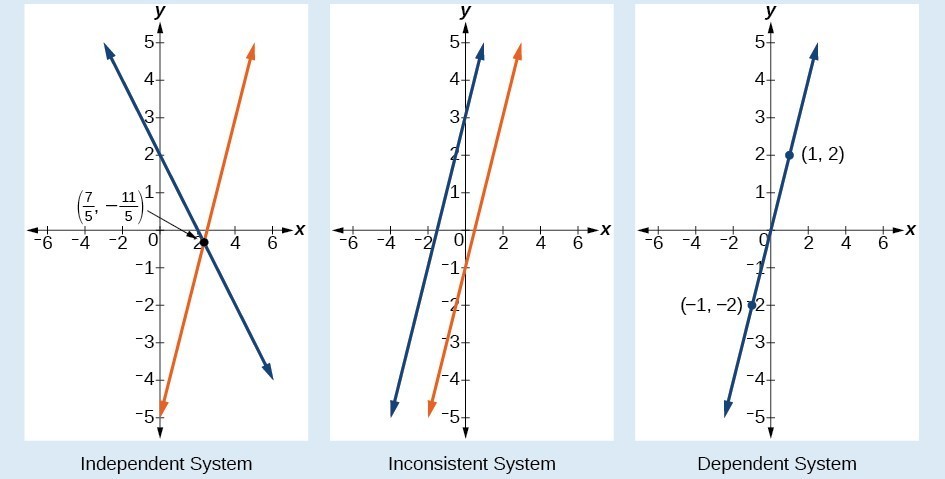
The independent and dependent systems are also consistent because they both have at least one solution.
How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
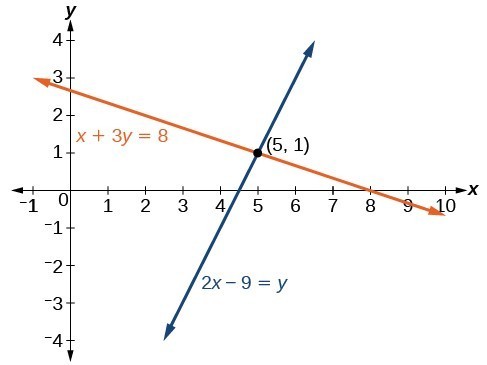
Example
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.
Show Solution
In the following video, we will show another example of how to verify whether an ordered pair is a solution to a system of equations.
Solving Systems of Equations by Graphing
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
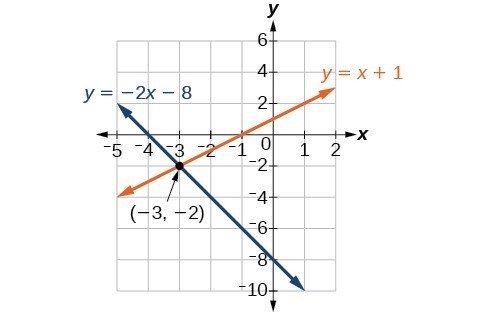
Example
Solve the following system of equations by graphing. Identify the type of system.
[latex]\begin{array}{c}2x+y=-8\\ x-y=-1\end{array}[/latex]
Show Solution
Graphing can be used if the system is inconsistent or dependent. In both cases, we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.
In the following video, we show another example of how to identify whether a graphed system has a solution and identify what type of solution is represented.
In our next video, we show how to solve a system of equations by first graphing the lines and then identifying the solution the system has.
Solving Systems of Equations by Substitution
Solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. We will consider two more methods of solving a system of linear equations that are more precise than graphing. One such method is solving a system of equations by the substitution method, in which we solve one of the equations for one variable and then substitute the result into the second equation to solve for the second variable. Recall that we can solve for only one variable at a time, which is the reason the substitution method is both valuable and practical.
How To: Given a system of two equations in two variables, solve using the substitution method.
- Solve one of the two equations for one of the variables in terms of the other.
- Substitute the expression for this variable into the second equation, then solve for the remaining variable.
- Substitute that solution into either of the original equations to find the value of the first variable. If possible, write the solution as an ordered pair.
- Check the solution in both equations.
Example: Solving a System of Equations in Two Variables by Substitution
Solve the following system of equations by substitution.
[latex]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]
In the following video, you will be given an example of solving a system of two equations using the substitution method.
If you had chosen the other equation to start with in the previous example, you would still be able to find the same solution. It is really a matter of preference, because sometimes solving for a variable will result in having to work with fractions. As you become more experienced with algebra, you will be able to anticipate what choices will lead to more desirable outcomes.
tip for success
Since the concepts in this module rely heavily upon those from earlier modules, feel free to go back to review information you may not have fully obtained the first time. Math is best digested over time with repetition that leads to deeper appreciation of the ideas involved.
Additional practice will also help you build skills using learned concepts in creative ways to make good choices of technique in different situations.
Try It
You can use an online graphing calculator to help you solve a system of equations by substitution. We will use the following system to show you how:
[latex]\begin{align}x&=y+3 \\ 4&=3x - 2y \end{align}[/latex]
First, solve both equations for y:
[latex]\begin{align}y&=x-3 \\ y&=\frac{3}{2}x - 2 \end{align}[/latex]
Now enter [latex]x-3=\frac{3}{2}x - 2[/latex] into the calculator. You will see that calculator has provided you with [latex]x = -2[/latex].
You now can substitute [latex]x = -2[/latex] into both equations. If you get the same result for both, you have found an ordered pair solution. Give it a try.
Q & A
Can the substitution method be used to solve any linear system in two variables?
Yes, but the method works best if one of the equations contains a coefficient of 1 or –1 so that we do not have to deal with fractions.
The following video is ~10 minutes long and provides a mini-lesson on using the substitution method to solve a system of linear equations. We present three different examples, and also use a graphing tool to help summarize the solution for each example.
Solving Systems of Equations in Two Variables by the Addition Method
A third method of solving systems of linear equations is the addition method, this method is also called the elimination method. In this method, we add two terms with the same variable, but opposite coefficients, so that the sum is zero. Of course, not all systems are set up with the two terms of one variable having opposite coefficients. Often we must adjust one or both of the equations by multiplication so that one variable will be eliminated by addition.
How To: Given a system of equations, solve using the addition method.
- Write both equations with x– and y-variables on the left side of the equal sign and constants on the right.
- Write one equation above the other, lining up corresponding variables. If one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, add the equations together, eliminating one variable. If not, use multiplication by a nonzero number so that one of the variables in the top equation has the opposite coefficient of the same variable in the bottom equation, then add the equations to eliminate the variable.
- Solve the resulting equation for the remaining variable.
- Substitute that value into one of the original equations and solve for the second variable.
- Check the solution by substituting the values into the other equation.
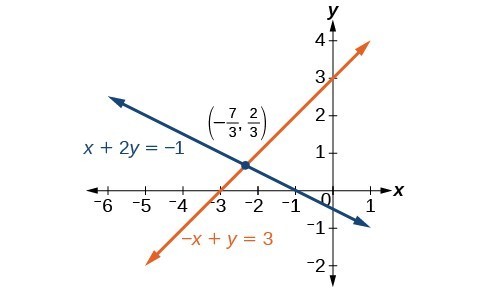
Example: Solving a System by the Addition Method
Solve the given system of equations by addition.
[latex]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]
In the following video, you will see another example of how to use the method of elimination to solve a system of linear equations.
Try it
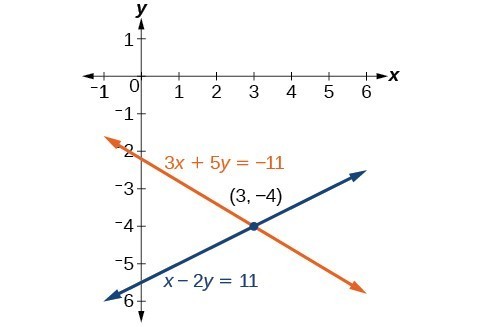
Example: Using the Addition Method When Multiplication of One Equation Is Required
Solve the given system of equations by the addition method.
[latex]\begin{align}3x+5y&=-11 \\ x - 2y&=11 \end{align}[/latex]
Below is another video example of using the elimination method to solve a system of linear equations when multiplication of one equation is required.
tip for success
Remember to work through the given examples and practice problems on paper and more than once to deepen your understanding.
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x - 7y&=2\\ 3x+y&=-20\end{align}[/latex]
Example: Using the Addition Method When Multiplication of Both Equations Is Required
Solve the given system of equations in two variables by addition.
[latex]\begin{align}2x+3y&=-16 \\ 5x - 10y&=30\end{align}[/latex]
Example: Using the Addition Method in Systems of Equations Containing Fractions
Solve the given system of equations in two variables by addition.
[latex]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1mm] \frac{x}{2}-\frac{y}{4}&=1 \end{align}[/latex]
In the following video, you will find one more example of using the elimination method to solve a system; this one has coefficients that are fractions.
Try It
Solve the system of equations by addition.
[latex]\begin{align}2x+3y&=8\\ 3x+5y&=10\end{align}[/latex]
in the following video we present more examples of how to use the addition (elimination) method to solve a system of two linear equations.