An inequality is a mathematical statement that compares two expressions using a phrase such as greater than or less than. Special symbols are used in these statements. In algebra, inequalities are used to describe sets of values, as opposed to single values, of a variable. Sometimes, several numbers will satisfy an inequality, but at other times infinitely many numbers may provide solutions. Rather than try to list a possibly infinitely large set of numbers, mathematicians have developed some efficient ways to describe such large lists.

Inequality Symbols

One way to represent such a list of numbers, an inequality, is by using an inequality symbol:

• [latex]{x}\lt{9}[/latex] indicates the list of numbers that are less than [latex]9[/latex]. Since this list is infinite, it would be impossilbe to list all numbers less than [latex]9[/latex].
• [latex]-5\le{t}[/latex] indicates all the numbers that are greater than or equal to [latex]-5[/latex].

If you were to read the above statement from left to right, it would translate as [latex]-5[/latex] is less than or equal to t. The direction of the symbol is dependent upon the statement you wish to make. For example, the following statements are equivalent. Both represent the list of all numbers less than 9. Note how the open end of the inequality symbol faces the larger value while the smaller, pointy end points to the smaller of the values:

• [latex]{x}\lt{9}[/latex]
• [latex]{9}\gt{x}[/latex]

Here’s another way of looking at is:

• [latex]x\lt5[/latex] means all the real numbers that are less than 5, whereas;
• [latex]5\lt{x}[/latex] means that 5 is less than x, or we could rewrite this with the x on the left: [latex]x\gt{5}[/latex]. Note how the inequality is still pointing the same direction relative to x. This statement represents all the real numbers that are greater than 5 which is easier to interpret than 5 is less than x.

The box below shows the symbol, meaning, and an example for each inequality sign, as they would be translated reading from left to right.

The inequality [latex]x>y[/latex] can also be written as [latex]{y}<{x}[/latex]. The sides of any inequality can be switched as long as the inequality symbol between them is also reversed.

Graphing an Inequality

Another way to represent an inequality is by graphing it on a number line:

Below are three examples of inequalities and their graphs.  Graphs are often helpful for visualizing information.

[latex]x\leq -4[/latex]. This translates to all the real numbers on a number line that are less than or equal to [latex]4[/latex].

[latex]{x}\geq{-3}[/latex]. This translates to all the real numbers on the number line that are greater than or equal to -3.

Each of these graphs begins with a circle—either an open or closed (shaded) circle. This point is often called the end point of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to [latex] \displaystyle \left(\geq\right) [/latex] or less than or equal to [latex] \displaystyle \left(\leq\right) [/latex]. The end point is part of the solution. An open circle is used for greater than (>) or less than (<). The end point is not part of the solution. When the end point is not included in the solution, we often say we have strict inequality rather than inequality with equality.

The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. For example, notice that for the graph of [latex] \displaystyle x\geq -3[/latex] shown above, the end point is [latex]−3[/latex], represented with a closed circle since the inequality is greater than or equal to [latex]−3[/latex]. The blue line is drawn to the right on the number line because the values in this area are greater than [latex]−3[/latex]. The arrow at the end indicates that the solutions continue infinitely.

Example

Graph the inequality [latex]x\ge 4[/latex]

Show Solution

We can use a number line as shown. Because the values for [latex]x[/latex] include [latex]4[/latex], we place a solid dot on the number line at [latex]4[/latex].

Then we draw a line that begins at [latex]x=4[/latex] and, as indicated by the arrowhead, continues to positive infinity, which illustrates that the solution set includes all real numbers greater than or equal to [latex]4[/latex].

This video shows an example of how to draw the graph of an inequality.

Example

Write an inequality describing all the real numbers on the number line that are strictly less than [latex]2[/latex]. Then draw the corresponding graph.

Show Solution

We need to start from the left and work right, so we start from negative infinity and end at [latex]2[/latex]. We will not include either because infinity is not a number, and the inequality does not include [latex]2[/latex].

Inequality: [latex]x\lt2[/latex]

To draw the graph, place an open dot on the number line first, and then draw a line extending to the left. Draw an arrow at the leftmost point of the line to indicate that it continues for infinity.

Represent Inequalities Using Interval Notation

Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. With this convention, sets are built with parentheses or brackets, each having a distinct meaning. The solutions to [latex]x\geq 4[/latex] are represented as [latex]\left[4,\infty \right)[/latex]. This method is widely used and will be present in other math courses you may take.

The main concept to remember is that parentheses represent solutions greater or less than the number, and brackets represent solutions that are greater than or equal to or less than or equal to the number. Use parentheses to represent infinity or negative infinity, since positive and negative infinity are not numbers in the usual sense of the word and, therefore, cannot be “equaled.” A few examples of an interval, or a set of numbers in which a solution falls, are [latex]\left[-2,6\right)[/latex], or all numbers between [latex]-2[/latex] and [latex]6[/latex], including [latex]-2[/latex], but not including [latex]6[/latex]; [latex]\left(-1,0\right)[/latex], all real numbers between, but not including [latex]-1[/latex] and [latex]0[/latex]; and [latex]\left(-\infty,1\right][/latex], all real numbers less than and including [latex]1[/latex]. The table below outlines the possibilities. Remember to read inequalities from left to right, just like text.

The table below describes all the possible inequalities that can occur and how to write them using interval notation, where a and b are real numbers.

Think About It

In the previous examples you were given an inequality or a description of one with words and asked to draw the corresponding graph and write the interval. In this example you are given an interval and asked to write the inequality and draw the graph.

Given [latex]\left(-\infty,10\right)[/latex], write the associated inequality and draw the graph.

In the box below, write down whether you think it will be easier to draw the graph first or write the inequality first.

 

Show Solution

We will draw the graph first.

The interval reads “all real numbers less than 10,” so we will start by placing an open dot on 10 and drawing a line to the left with an arrow indicating the solution continues to negative infinity.

To write the inequality, we will use < since the parentheses indicate that 10 is not included. [latex]x<10[/latex]

In the following video, you will see examples of how to write inequalities in the three ways presented here: as an inequality, in interval notation, and with a graph.

Multiplication and Division Properties of Inequality

Solving inequalities is very similar to solving equations, except you have to reverse the inequality symbols when you multiply or divide both sides of an inequality by a negative number. There are three ways to represent solutions to inequalities: an interval, a graph, and an inequality. Because there is usually more than one solution to an inequality, when you check your answer, you should check the end point and one other value to check the direction of the inequality. When we work with inequalities, we can usually treat them similar to but not exactly as we treat equations. We can use the addition property and the multiplication property to help us solve them. The one exception is when we multiply or divide by a negative number; doing so reverses the inequality symbol.

The following table illustrates how the multiplication property is applied to inequalities, and how multiplication by a negative reverses the inequality:

The following table illustrates how the division property is applied to inequalities, and how dividing by a negative reverses the inequality:

In the first example, we will show how to apply the multiplication and division properties of equality to solve some inequalities.

Solve Inequalities Using the Addition Property

When we solve equations we may need to add or subtract in order to isolate the variable, the same is true for inequalities. There are no special behaviors to watch out for when using the addition property to solve inequalities.

The following table illustrates how the addition property applies to inequalities.

These properties also apply to [latex]a\le b[/latex], [latex]a>b[/latex], and [latex]a\ge b[/latex].

In our next example we will use the addition property to solve inequalities.

The following video shows examples of solving single-step inequalities using the multiplication and addition properties.

The following video shows examples of solving inequalities with the variable on the right side.

Solve Multi-Step Inequalities

As the previous examples have shown, we can perform the same operations on both sides of an inequality, just as we do with equations. To isolate the variable and solve, we combine like terms and perform operations with the multiplication and addition properties.

In the next example we solve an inequality that contains fractions, not how we need to reverse the inequality sign at the end because we multiply by a negative.

Use Interval Notation to Describe Sets of Numbers as Intersections and Unions

When two inequalities are joined by the word and, the solution of the compound inequality occurs when both inequalities are true at the same time. It is the overlap, or intersection, of the solutions for each inequality. When the two inequalities are joined by the word or, the solution of the compound inequality occurs when either of the inequalities is true. The solution is the combination, or union, of the two individual solutions.

In this section we will learn how to solve compound inequalities that are joined with the words AND and OR. First, it will help to see some examples of inequalities, intervals, and graphs of compound inequalities. This will help you describe the solutions to compound inequalities properly.

Venn diagrams use the concept of intersections and unions to compare two or more things. For example, this Venn diagram shows the intersection of people who are breaking your heart and those who are shaking your confidence daily. Apparently Cecilia has both of these qualities; therefore, she is the intersection of the two.

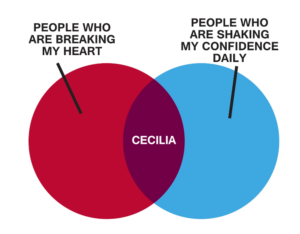
In mathematical terms, consider the inequality [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. How would we interpret what numbers x can be, and what would the interval look like?

In words, x must be less than [latex]6[/latex], and at the same time, it must be greater than [latex]2[/latex]. This is much like the Venn diagram above where Cecilia is at once breaking your heart and shaking your confidence daily. Now look at a graph to see what numbers are possible with these constraints.

The numbers that are shared by both lines on the graph are called the intersection of the two inequalities [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. This is called a bounded inequality and is written as [latex]2\lt{x}\lt6[/latex]. Think about that one for a minute. x must be less than [latex]6[/latex] and greater than two—the values for x will fall between two numbers. In interval notation, this looks like [latex]\left(2,6\right)[/latex]. The graph would look like this:

On the other hand, if you need to represent two things that don’t share any common elements or traits, you can use a union. The following Venn diagram shows two things that share no similar traits or elements but are often considered in the same application, such as online shopping or banking.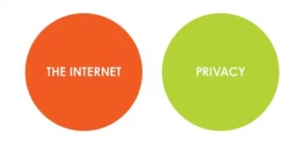

In mathematical terms, for example, [latex]x>6[/latex] or [latex]x<2[/latex] is an inequality joined by the word or. Using interval notation, we can describe each of these inequalities separately:

[latex]x\gt6[/latex] is the same as [latex]\left(6, \infty\right)[/latex] and [latex]x<2[/latex] is the same as [latex]\left(-\infty, 2\right)[/latex]. If we are describing solutions to inequalities, what effect does the or have? We are saying that solutions are either real numbers less than two or real numbers greater than [latex]6[/latex]. Can you see why we need to write them as two separate intervals? Let us look at a graph to get a clear picture of what is going on.

When you place both of these inequalities on a graph, we can see that they share no numbers in common. As mentioned above, this is what we call a union. The interval notation associated with a union is a big U, so instead of writing or, we join our intervals with a big U, like this:

[latex]\left(-\infty, 2\right)\cup\left(6, \infty\right)[/latex]

It is common convention to construct intervals starting with the value that is furthest left on the number line as the left value, such as [latex]\left(2,6\right)[/latex], where [latex]2[/latex] is less than [latex]6[/latex]. The number on the right should be greater than the number on the left.

Example

Draw the graph of the compound inequality [latex]x\gt3[/latex] or [latex]x\le4[/latex] and describe the set of x-values that will satisfy it with an interval.

Show Solution

The graph of [latex]x\gt3[/latex] has an open circle on [latex]3[/latex] and a blue arrow drawn to the right to contain all the numbers greater than [latex]3[/latex].

The graph of [latex]x\le4[/latex] has a closed circle at 4 and a red arrow to the left to contain all the numbers less than [latex]4[/latex].

What do you notice about the graph that combines these two inequalities?

Since this compound inequality is an or statement, it includes all of the numbers in each of the solutions. In this case, the solution is all the numbers on the number line. (The region of the line greater than [latex]3[/latex] and less than or equal to [latex]4[/latex] is shown in purple because it lies on both of the original graphs.) The solution to the compound inequality [latex]x\gt3[/latex] or [latex]x\le4[/latex] is the set of all real numbers and can be described in interval notation as [latex]\left(-\infty, \infty\right)[/latex]

In the following video you will see two examples of how to express inequalities involving or graphically and as an interval.

Example

Draw a graph of the compound inequality: [latex]x\lt5[/latex] and [latex]x\ge−1[/latex], and describe the set of x-values that will satisfy it with an interval.

Show Solution

The graph of each individual inequality is shown in color.

Since the word and joins the two inequalities, the solution is the overlap of the two solutions. This is where both of these statements are true at the same time.

The solution to this compound inequality is shown below.

Notice that this is a bounded inequality. You can rewrite [latex]x\ge−1\,\text{and }x\le5[/latex] as [latex]−1\le x\le 5[/latex] since the solution is between [latex]−1[/latex] and [latex]5[/latex], including [latex]−1[/latex]. You read [latex]−1\le x\lt{5}[/latex] as “x is greater than or equal to [latex]−1[/latex] and less than [latex]5[/latex].” You can rewrite an and statement this way only if the answer is between two numbers. The set of solutions to this inequality can be written in interval notation like this: [latex]\left[{-1},{5}\right)[/latex]

Example

Draw the graph of the compound inequality [latex]2x+1\lt{-5}[/latex] and [latex]4x-3\gt{9}[/latex], and describe the set of x-values that will satisfy it with an interval.

Show Solution

First, we must solve each inequality for [latex]x[/latex]:
[latex]2x+1\lt{-5}[/latex] and [latex]4x-3\gt{9}[/latex]
[latex]2x\lt{-6}[/latex] and [latex]4x\gt{12}[/latex]
[latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex]
Now, draw a graph. We are looking for values for x that will satisfy both inequalities since they are joined with the word and.

In this case, there are no shared x-values, and therefore there is no intersection for these two inequalities. We can write “no solution,” or DNE.

The following video presents two examples of how to draw inequalities involving and as well as write the corresponding intervals.