Section 4.3: Properties of Rational Functions

Learning Outcomes

  • Solve applied problems involving rational functions.
  • Find the domains of rational functions.
  • Identify vertical and horizontal asymptotes.
  • Identify slant asymptotes.

 Find the domains of rational functions

A vertical asymptote represents a value at which a rational function is undefined, so that value is not in the domain of the function. A rational function cannot have values in its domain that cause the denominator to equal zero. In general, to find the domain of a rational function, we need to determine which inputs would cause division by zero.

A General Note: Domain of a Rational Function

The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.

How To: Given a rational function, find the domain.

  1. Set the denominator equal to zero.
  2. Solve to find the x-values that cause the denominator to equal zero.
  3. The domain is all real numbers except those found in Step 2.

Example 1: Finding the Domain of a Rational Function

Find the domain of [latex]f\left(x\right)=\frac{x+3}{{x}^{2}-9}[/latex].

Try It

Find the domain of [latex]f\left(x\right)=\frac{4x}{5\left(x - 1\right)\left(x - 5\right)}[/latex].

 Identify vertical asymptotes

By looking at the graph of a rational function, we can investigate its local behavior and easily see whether there are asymptotes. We may even be able to approximate their location. Even without the graph, however, we can still determine whether a given rational function has any asymptotes, and calculate their location.

Vertical Asymptotes

The vertical asymptotes of a rational function may be found by examining the factors of the denominator that are not common to the factors in the numerator. Vertical asymptotes occur at the zeros of such factors.

How To: Given a rational function, identify any vertical asymptotes of its graph.

  1. Factor the numerator and denominator.
  2. Note any restrictions in the domain of the function.
  3. Reduce the expression by canceling common factors in the numerator and the denominator.
  4. Note any values that cause the denominator to be zero in this simplified version. These are where the vertical asymptotes occur.
  5. Note any restrictions in the domain where asymptotes do not occur. These are removable discontinuities.

Example 2: Identifying Vertical Asymptotes

Find the vertical asymptotes of the graph of [latex]k\left(x\right)=\frac{5+2{x}^{2}}{2-x-{x}^{2}}[/latex].

Removable Discontinuities

Occasionally, a graph will contain a hole: a single point where the graph is not defined, indicated by an open circle. We call such a hole a removable discontinuity.

For example, the function [latex]f\left(x\right)=\frac{{x}^{2}-1}{{x}^{2}-2x - 3}[/latex] may be re-written by factoring the numerator and the denominator.

[latex]f\left(x\right)=\frac{\left(x+1\right)\left(x - 1\right)}{\left(x+1\right)\left(x - 3\right)}[/latex]

Notice that [latex]x+1[/latex] is a common factor to the numerator and the denominator. The zero of this factor, [latex]x=-1[/latex], is the location of the removable discontinuity. Notice also that [latex]x - 3[/latex] is not a factor in both the numerator and denominator. The zero of this factor, [latex]x=3[/latex], is the vertical asymptote.

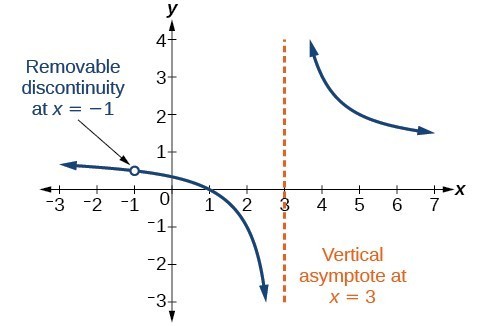
Graph of f(x)=(x^2-1)/(x^2-2x-3) with its vertical asymptote at x=3 and a removable discontinuity at x=-1.

Figure 3

A General Note: Removable Discontinuities of Rational Functions

A removable discontinuity occurs in the graph of a rational function at [latex]x=a[/latex] if a is a zero for a factor in the denominator that is common with a factor in the numerator. We factor the numerator and denominator and check for common factors. If we find any, we set the common factor equal to 0 and solve. This is the location of the removable discontinuity. This is true if the multiplicity of this factor is greater than or equal to that in the denominator. If the multiplicity of this factor is greater in the denominator, then there is still an asymptote at that value.

Example 3: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Find the vertical asymptotes and removable discontinuities of the graph of [latex]k\left(x\right)=\frac{x - 2}{{x}^{2}-4}[/latex].

Try It

Find the vertical asymptotes and removable discontinuities of the graph of [latex]f\left(x\right)=\frac{{x}^{2}-25}{{x}^{3}-6{x}^{2}+5x}[/latex].

Try It

Identify horizontal asymptotes

While vertical asymptotes describe the behavior of a graph as the output gets very large or very small, horizontal asymptotes help describe the behavior of a graph as the input gets very large or very small. Recall that a polynomial’s end behavior will mirror that of the leading term. Likewise, a rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.

There are three distinct outcomes when checking for horizontal asymptotes:

Case 1: If the degree of the denominator > degree of the numerator, there is a horizontal asymptote at y = 0.

[latex]\text{Example: }f\left(x\right)=\frac{4x+2}{{x}^{2}+4x - 5}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx \frac{4x}{{x}^{2}}=\frac{4}{x}[/latex]. This tells us that, as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=\frac{4}{x}[/latex], and the outputs will approach zero, resulting in a horizontal asymptote at y = 0. Note that this graph crosses the horizontal asymptote.

 

Graph of f(x)=(4x+2)/(x^2+4x-5) with its vertical asymptotes at x=-5 and x=1 and its horizontal asymptote at y=0.

Figure 5. Horizontal Asymptote y = 0 when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne{0}\text{ where degree of }p<\text{degree of q}[/latex].

Case 2: If the degree of the denominator < degree of the numerator by one, we get a slant asymptote.

[latex]\text{Example: }f\left(x\right)=\frac{3{x}^{2}-2x+1}{x - 1}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{x}=3x[/latex]. This tells us that as the inputs increase or decrease without bound, this function will behave similarly to the function [latex]g\left(x\right)=3x[/latex]. As the inputs grow large, the outputs will grow and not level off, so this graph has no horizontal asymptote. However, the graph of [latex]g\left(x\right)=3x[/latex] looks like a diagonal line, and since f will behave similarly to g, it will approach a line close to [latex]y=3x[/latex]. This line is a slant asymptote.

To find the equation of the slant asymptote, divide [latex]\frac{3{x}^{2}-2x+1}{x - 1}[/latex]. The quotient is [latex]3x+1[/latex], and the remainder is 2. The slant asymptote is the graph of the line [latex]g\left(x\right)=3x+1[/latex].
Graph of f(x)=(3x^2-2x+1)/(x-1) with its vertical asymptote at x=1 and a slant asymptote aty=3x+1.

Figure 6. Slant Asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex] where degree of [latex]p>\text{ degree of }q\text{ by }1[/latex].

Case 3: If the degree of the denominator = degree of the numerator, there is a horizontal asymptote at [latex]y=\frac{{a}_{n}}{{b}_{n}}[/latex], where [latex]{a}_{n}[/latex] and [latex]{b}_{n}[/latex] are the leading coefficients of [latex]p\left(x\right)[/latex] and [latex]q\left(x\right)[/latex] for [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0[/latex].

[latex]\text{Example: }f\left(x\right)=\frac{3{x}^{2}+2}{{x}^{2}+4x - 5}[/latex]

In this case, the end behavior is [latex]f\left(x\right)\approx \frac{3{x}^{2}}{{x}^{2}}=3[/latex]. This tells us that as the inputs grow large, this function will behave like the function [latex]g\left(x\right)=3[/latex], which is a horizontal line. As [latex]x\to \pm \infty ,f\left(x\right)\to 3[/latex], resulting in a horizontal asymptote at y = 3. Note that this graph crosses the horizontal asymptote.

Graph of f(x)=(3x^2+2)/(x^2+4x-5) with its vertical asymptotes at x=-5 and x=1 and its horizontal asymptote at y=3.

Figure 7. Horizontal Asymptote when [latex]f\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)},q\left(x\right)\ne 0\text{where degree of }p=\text{degree of }q[/latex].

Notice that, while the graph of a rational function will never cross a vertical asymptote, the graph may or may not cross a horizontal or slant asymptote. Also, although the graph of a rational function may have many vertical asymptotes, the graph will have at most one horizontal (or slant) asymptote.

It should be noted that, if the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the graph will mimic the behavior of the reduced end behavior fraction. For instance, if we had the function

[latex]f\left(x\right)=\frac{3{x}^{5}-{x}^{2}}{x+3}[/latex]

with end behavior

[latex]f\left(x\right)\approx \frac{3{x}^{5}}{x}=3{x}^{4}[/latex],

the end behavior of the graph would look similar to that of an even polynomial with a positive leading coefficient.

[latex]x\to \pm \infty , f\left(x\right)\to \infty [/latex]

A General Note: Horizontal Asymptotes of Rational Functions

The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.

  • Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.
  • Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
  • Degree of numerator is equal to degree of denominator: horizontal asymptote at ratio of leading coefficients.

Example 4: Identifying Horizontal and Slant Asymptotes

For the functions below, identify the horizontal or slant asymptote.

  1. [latex]g\left(x\right)=\frac{6{x}^{3}-10x}{2{x}^{3}+5{x}^{2}}[/latex]
  2. [latex]h\left(x\right)=\frac{{x}^{2}-4x+1}{x+2}[/latex]
  3. [latex]k\left(x\right)=\frac{{x}^{2}+4x}{{x}^{3}-8}[/latex]

Example 5: Identifying Horizontal Asymptotes

In the sugar concentration problem earlier, we created the equation [latex]C\left(t\right)=\frac{5+t}{100+10t}[/latex].

Find the horizontal asymptote and interpret it in context of the problem.

Example 6: Identifying Horizontal and Vertical Asymptotes

Find the horizontal and vertical asymptotes of the function

[latex]f\left(x\right)=\frac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex]

Try It

Find the vertical and horizontal asymptotes of the function:

[latex]f\left(x\right)=\frac{\left(2x - 1\right)\left(2x+1\right)}{\left(x - 2\right)\left(x+3\right)}[/latex]

A General Note: Intercepts of Rational Functions

A rational function will have a y-intercept when the input is zero, if the function is defined at zero. A rational function will not have a y-intercept if the function is not defined at zero.

Likewise, a rational function will have x-intercepts at the inputs that cause the output to be zero. Since a fraction is only equal to zero when the numerator is zero, x-intercepts can only occur when the numerator of the rational function is equal to zero.

Example 7: Finding the Intercepts of a Rational Function

Find the intercepts of [latex]f\left(x\right)=\frac{\left(x - 2\right)\left(x+3\right)}{\left(x - 1\right)\left(x+2\right)\left(x - 5\right)}[/latex].

Try It

Given the reciprocal squared function that is shifted right 3 units and down 4 units, write this as a rational function. Then, find the x– and y-intercepts and the horizontal and vertical asymptotes.

Try It

Writing Rational Functions

Now that we have analyzed the equations for rational functions and how they relate to a graph of the function, we can use information given by a graph to write the function. A rational function written in factored form will have an x-intercept where each factor of the numerator is equal to zero. (An exception occurs in the case of a removable discontinuity.) As a result, we can form a numerator of a function whose graph will pass through a set of x-intercepts by introducing a corresponding set of factors. Likewise, because the function will have a vertical asymptote where each factor of the denominator is equal to zero, we can form a denominator that will produce the vertical asymptotes by introducing a corresponding set of factors.

A General Note: Writing Rational Functions from Intercepts and Asymptotes

If a rational function has x-intercepts at [latex]x={x}_{1}, {x}_{2}, …, {x}_{n}[/latex], vertical asymptotes at [latex]x={v}_{1},{v}_{2},\dots ,{v}_{m}[/latex], and no [latex]{x}_{i}=\text{any }{v}_{j}[/latex], then the function can be written in the form:

[latex]f\left(x\right)=a\frac{{\left(x-{x}_{1}\right)}^{{p}_{1}}{\left(x-{x}_{2}\right)}^{{p}_{2}}\cdots {\left(x-{x}_{n}\right)}^{{p}_{n}}}{{\left(x-{v}_{1}\right)}^{{q}_{1}}{\left(x-{v}_{2}\right)}^{{q}_{2}}\cdots {\left(x-{v}_{m}\right)}^{{q}_{n}}}[/latex]

where the powers [latex]{p}_{i}[/latex] or [latex]{q}_{i}[/latex] on each factor can be determined by the behavior of the graph at the corresponding intercept or asymptote, and the stretch factor a can be determined given a value of the function other than the x-intercept or by the horizontal asymptote if it is nonzero.

How To: Given a graph of a rational function, write the function.

  1. Determine the factors of the numerator. Examine the behavior of the graph at the x-intercepts to determine the zeroes and their multiplicities. (This is easy to do when finding the “simplest” function with small multiplicities—such as 1 or 3—but may be difficult for larger multiplicities—such as 5 or 7, for example.)
  2. Determine the factors of the denominator. Examine the behavior on both sides of each vertical asymptote to determine the factors and their powers.
  3. Use any clear point on the graph to find the stretch factor.

Example 8: Writing a Rational Function from Intercepts and Asymptotes

Write an equation for the rational function shown in Figure 23.

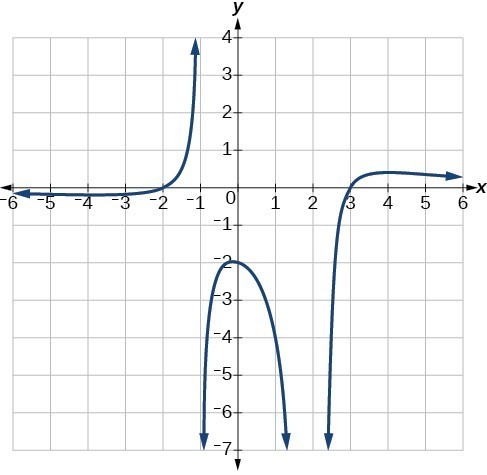
Graph of a rational function.

Figure 10

Key Equations

Rational Function [latex]f\left(x\right)=\dfrac{P\left(x\right)}{Q\left(x\right)}=\dfrac{{a}_{p}{x}^{p}+{a}_{p - 1}{x}^{p - 1}+…+{a}_{1}x+{a}_{0}}{{b}_{q}{x}^{q}+{b}_{q - 1}{x}^{q - 1}+…+{b}_{1}x+{b}_{0}}, Q\left(x\right)\ne 0[/latex]

Key Concepts

  • A function that levels off at a horizontal value has a horizontal asymptote. A function can have more than one vertical asymptote.
  • The domain of a rational function includes all real numbers except those that cause the denominator to equal zero.
  • The vertical asymptotes of a rational function will occur where the denominator of the function is equal to zero and the numerator is not zero.
  • A removable discontinuity might occur in the graph of a rational function if an input causes both numerator and denominator to be zero.
  • A rational function’s end behavior will mirror that of the ratio of the leading terms of the numerator and denominator functions.
  • If a rational function has x-intercepts at [latex]x={x}_{1},{x}_{2},\dots ,{x}_{n}[/latex], vertical asymptotes at [latex]x={v}_{1},{v}_{2},\dots ,{v}_{m}[/latex], and no [latex]{x}_{i}=\text{any }{v}_{j}[/latex], then the function can be written in the form [latex]f\left(x\right)=a\frac{{\left(x-{x}_{1}\right)}^{{p}_{1}}{\left(x-{x}_{2}\right)}^{{p}_{2}}\cdots {\left(x-{x}_{n}\right)}^{{p}_{n}}}{{\left(x-{v}_{1}\right)}^{{q}_{1}}{\left(x-{v}_{2}\right)}^{{q}_{2}}\cdots {\left(x-{v}_{m}\right)}^{{q}_{n}}}[/latex]

Glossary

horizontal asymptote
a horizontal line y = b where the graph approaches the line as the inputs increase or decrease without bound.
rational function
a function that can be written as the ratio of two polynomials
removable discontinuity
a single point at which a function is undefined that, if filled in, would make the function continuous; it appears as a hole on the graph of a function
vertical asymptote
a vertical line x = a where the graph tends toward positive or negative infinity as the inputs approach a

 

Section 4.3 Homework Exercises

1. What is the fundamental difference in the algebraic representation of a polynomial function and a rational function?

2. What is the fundamental difference in the graphs of polynomial functions and rational functions?

3. If the graph of a rational function has a removable discontinuity, what must be true of the functional rule?

4. Can a graph of a rational function have no vertical asymptote? If so, how?

5. Can a graph of a rational function have no x-intercepts? If so, how?

For the following exercises, find the domain of the rational functions.

6. [latex]f\left(x\right)=\frac{x - 1}{x+2}[/latex]

7. [latex]f\left(x\right)=\frac{x+1}{{x}^{2}-1}[/latex]

8. [latex]f\left(x\right)=\frac{{x}^{2}+4}{{x}^{2}-2x - 8}[/latex]

9. [latex]f\left(x\right)=\frac{{x}^{2}+4x - 3}{{x}^{4}-5{x}^{2}+4}[/latex]

For the following exercises, find the domain, vertical asymptotes, and horizontal asymptotes of the functions.

10. [latex]f\left(x\right)=\frac{4}{x - 1}[/latex]

11. [latex]f\left(x\right)=\frac{2}{5x+2}[/latex]

12. [latex]f\left(x\right)=\frac{x}{{x}^{2}-9}[/latex]

13. [latex]f\left(x\right)=\frac{x}{{x}^{2}+5x - 36}[/latex]

14. [latex]f\left(x\right)=\frac{3+x}{{x}^{3}-27}[/latex]

15. [latex]f\left(x\right)=\frac{3x - 4}{{x}^{3}-16x}[/latex]

16. [latex]f\left(x\right)=\frac{{x}^{2}-1}{{x}^{3}+9{x}^{2}+14x}[/latex]

17. [latex]f\left(x\right)=\frac{x+5}{{x}^{2}-25}[/latex]

18. [latex]f\left(x\right)=\frac{x - 4}{x - 6}[/latex]

19. [latex]f\left(x\right)=\frac{4 - 2x}{3x - 1}[/latex]

For the following exercises, find the x– and y-intercepts for the functions.

20. [latex]f\left(x\right)=\frac{x+5}{{x}^{2}+4}[/latex]

21. [latex]f\left(x\right)=\frac{x}{{x}^{2}-x}[/latex]

22. [latex]f\left(x\right)=\frac{{x}^{2}+8x+7}{{x}^{2}+11x+30}[/latex]

23. [latex]f\left(x\right)=\frac{{x}^{2}+x+6}{{x}^{2}-10x+24}[/latex]

24. [latex]f\left(x\right)=\frac{94 - 2{x}^{2}}{3{x}^{2}-12}[/latex]

For the following exercises, describe the local and end behavior of the functions.

25. [latex]f\left(x\right)=\frac{x}{2x+1}[/latex]

26. [latex]f\left(x\right)=\frac{2x}{x - 6}[/latex]

27. [latex]f\left(x\right)=\frac{-2x}{x - 6}[/latex]

28. [latex]f\left(x\right)=\frac{{x}^{2}-4x+3}{{x}^{2}-4x - 5}[/latex]

29. [latex]f\left(x\right)=\frac{2{x}^{2}-32}{6{x}^{2}+13x - 5}[/latex]

For the following exercises, find the slant asymptote of the functions.

30. [latex]f\left(x\right)=\frac{24{x}^{2}+6x}{2x+1}[/latex]

31. [latex]f\left(x\right)=\frac{4{x}^{2}-10}{2x - 4}[/latex]

32. [latex]f\left(x\right)=\frac{81{x}^{2}-18}{3x - 2}[/latex]

33. [latex]f\left(x\right)=\frac{6{x}^{3}-5x}{3{x}^{2}+4}[/latex]

34. [latex]f\left(x\right)=\frac{{x}^{2}+5x+4}{x - 1}[/latex]

For the following exercises, write an equation for a rational function with the given characteristics.

35. Vertical asymptotes at x = 5 and x = –5, x-intercepts at [latex]\left(2,0\right)[/latex] and [latex]\left(-1,0\right)[/latex], y-intercept at [latex]\left(0,4\right)[/latex]

36. Vertical asymptotes at [latex]x=-4[/latex] and [latex]x=-1[/latex], x-intercepts at [latex]\left(1,0\right)[/latex] and [latex]\left(5,0\right)[/latex], y-intercept at [latex]\left(0,7\right)[/latex]

37. Vertical asymptotes at [latex]x=-4[/latex] and [latex]x=-5[/latex], x-intercepts at [latex]\left(4,0\right)[/latex] and [latex]\left(-6,0\right)[/latex], Horizontal asymptote at [latex]y=7[/latex]

38. Vertical asymptotes at [latex]x=-3[/latex] and [latex]x=6[/latex], x-intercepts at [latex]\left(-2,0\right)[/latex] and [latex]\left(1,0\right)[/latex], Horizontal asymptote at [latex]y=-2[/latex]

39. Vertical asymptote at [latex]x=-1[/latex], Double zero at [latex]x=2[/latex], y-intercept at [latex]\left(0,2\right)[/latex]

40. Vertical asymptote at [latex]x=3[/latex], Double zero at [latex]x=1[/latex], y-intercept at [latex]\left(0,4\right)[/latex]

For the following exercises, use the graphs to write an equation for the function.

41.
Graph of a rational function with vertical asymptotes at x=-3 and x=4.

42.
Graph of a rational function with vertical asymptotes at x=-3 and x=4.

43.
Graph of a rational function with vertical asymptotes at x=-3 and x=3.

44.
Graph of a rational function with vertical asymptotes at x=-3 and x=4.

45.
Graph of a rational function with vertical asymptote at x=1.

46.

Graph of a rational function with vertical asymptote at x=-2.

47.
Graph of a rational function with vertical asymptotes at x=-3 and x=2.

48.
Graph of a rational function with vertical asymptotes at x=-2 and x=4.

For the following exercises, make tables to show the behavior of the function near the vertical asymptote and reflecting the horizontal asymptote

49. [latex]f\left(x\right)=\frac{1}{x - 2}[/latex]

50. [latex]f\left(x\right)=\frac{x}{x - 3}[/latex]

51. [latex]f\left(x\right)=\frac{2x}{x+4}[/latex]

52. [latex]f\left(x\right)=\frac{2x}{{\left(x - 3\right)}^{2}}[/latex]

53. [latex]f\left(x\right)=\frac{{x}^{2}}{{x}^{2}+2x+1}[/latex]

For the following exercises, identify the removable discontinuity.

54. [latex]f\left(x\right)=\frac{{x}^{3}+1}{x+1}[/latex]

55. [latex]f\left(x\right)=\frac{{x}^{2}+x - 6}{x - 2}[/latex]

56. [latex]f\left(x\right)=\frac{2{x}^{2}+5x - 3}{x+3}[/latex]

57. [latex]f\left(x\right)=\frac{{x}^{3}+{x}^{2}}{x+1}[/latex]