Finding Function Values from a Graph

In this section we will evaluate functions using its graph. Evaluating a function using a graph also requires finding the corresponding output value for a given input value, only in this case, we find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).

Example 1: Reading Function Values from a Graph

Given the graph in Figure 1,

1. Evaluate [latex]f\left(2\right)[/latex].
2. Solve [latex]f\left(x\right)=4[/latex].
3. Is [latex]f\left(-0.5\right)[/latex] positive or negative?
4. Find the x- and y-intercepts.

 

 

 

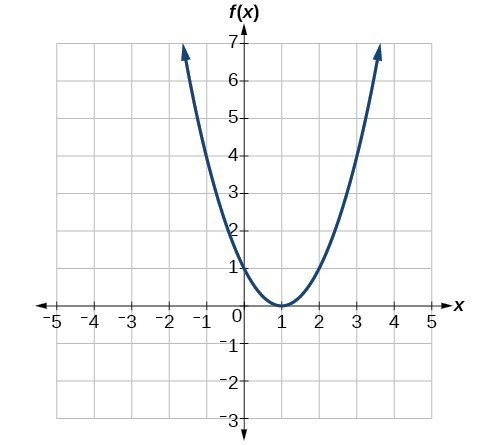
Figure 1

Show Solution

1. To evaluate [latex]f\left(2\right)[/latex], locate the point on the curve where [latex]x=2[/latex], then read the y-coordinate of that point. The point has coordinates [latex]\left(2,1\right)[/latex], so [latex]f\left(2\right)=1[/latex]. See Figure 2.
   

   

   Figure 2

2. To solve [latex]f\left(x\right)=4[/latex], we find the output value [latex]4[/latex] on the vertical axis. Moving horizontally along the line [latex]y=4[/latex], we locate two points of the curve with output value [latex]4:[/latex] [latex]\left(-1,4\right)[/latex] and [latex]\left(3,4\right)[/latex]. These points represent the two solutions to [latex]f\left(x\right)=4:[/latex] [latex]x=-1[/latex] or [latex]x=3[/latex]. This means [latex]f\left(-1\right)=4[/latex] and [latex]f\left(3\right)=4[/latex], or when the input is [latex]-1[/latex] or [latex]\text{3,}[/latex] the output is [latex]\text{4}\text{.}[/latex]See Figure 3.
   

   

   Figure 3

3. To find [latex]f\left(-0.5\right)[/latex], we need to go to -0.5 on the x-axis. Then we go up until we intersect the graph. From the graph, [latex]f\left(-0.5\right)\approx 2[/latex]. Therefore, we know that [latex]f\left(-0.5\right)[/latex] is positive.
4. The x-intercept is where the graph crosses the x-axis. We see that graph touches the x-axis only at one place, which is the point [latex](1,0)[/latex]. The y-intercept is where the graph crosses the y-axis. This occurs at the point [latex](0,1)[/latex].

Finding Domain and Range from Graphs

Next we will determine the domain and range of functions using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis. Keep in mind that if the graph continues beyond the portion of the graph we can see, the domain and range may be greater than the visible values. See Figure 4.

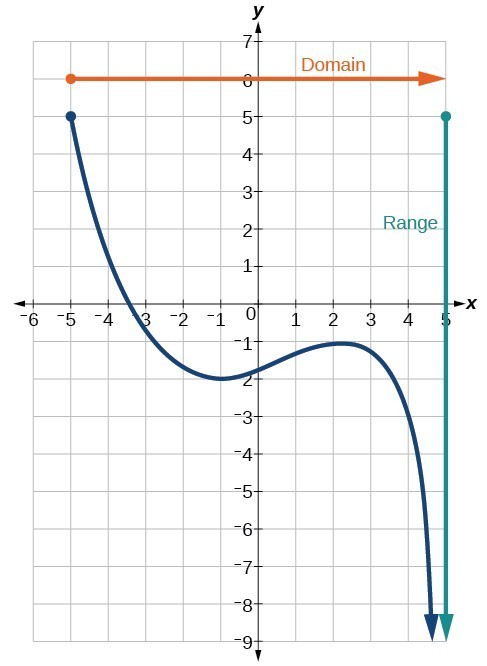
Figure 4

We can observe that the graph extends horizontally from [latex]-5[/latex] to the right without bound, so the domain is [latex]\left[-5,\infty \right)[/latex]. The vertical extent of the graph is all range values [latex]5[/latex] and below, so the range is [latex]\left(\mathrm{-\infty },5\right][/latex]. Note that the domain and range are always written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Example 2: Finding Domain and Range from a Graph

Find the domain and range of the function [latex]f[/latex] whose graph is shown in Figure 5.

Figure 5

 

Show Solution

We can observe that the horizontal extent of the graph is –3 to 1, so the domain of [latex]f[/latex] is [latex]\left(-3,1\right][/latex].

Figure 6

The vertical extent of the graph is 0 to –4, so the range is [latex]\left[-4,0\right)[/latex].

Try it

Key Concepts

• • • To evaluate a function on a graph, we determine the y-value for a corresponding x value.
    • To solve for a specific x-value on the graph, we determine the x values that yield the specific y values.
    • The domain of a graph includes all its x-values.
    • The range of a graph includes all its y-values.

Section 2.2 Homework Exercises

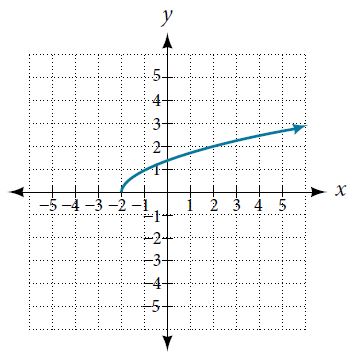
1. Given the following graph,
Evaluate [latex]f(−1)[/latex].
Solve for [latex]f(x)=3[/latex].
Find the domain.
Find the range.
Is [latex]f(-\frac{3}{2})[/latex] positive or negative?
What is the x-intercept?

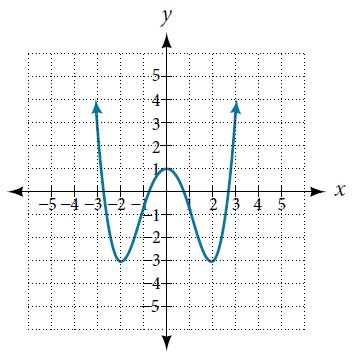
2. Given the following graph,
Evaluate [latex]f(0[/latex]).
Solve for [latex]f(x)=−3[/latex].
Find the domain.
Find the range.
Is [latex]f(-\frac{1}{2})[/latex] positive or negative?
Is [latex]f(1)[/latex] positive or negative?

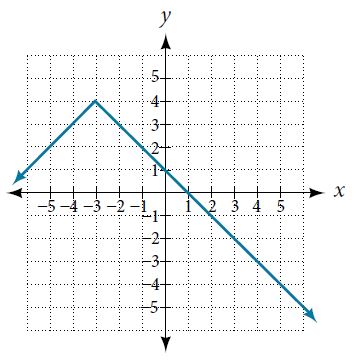
3. Given the following graph,
Evaluate [latex]f(4)[/latex].
Solve for [latex]f(x)=1[/latex].
Find the domain.
Find the range.
Is [latex]f(-2)[/latex] positive or negative?
Is [latex]f(3)[/latex] positive or negative?
What is the x-intercept?
What is the y-intercept?