Evaluating Compositions of the Form [latex]f^{−1}(g(x))[/latex]

Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form [latex]f^{−1}(g(x))[/latex]. For special values of x, we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is θ, making the other [latex]\frac{\pi}{2}−\theta[/latex]. Consider the sine and cosine of each angle of the right triangle in Figure 10.

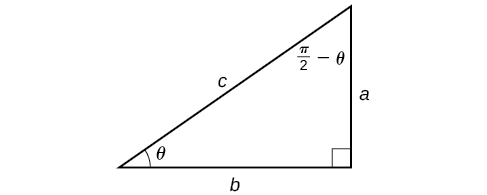
Figure 10. Right triangle illustrating the cofunction relationships

Because [latex]\cos\theta=\frac{b}{c}=\sin\left(\frac{\pi}{2}−\theta\right)[/latex], we have [latex]\sin^{−1}(\cos\theta)=\frac{\pi}{2}−\theta\text{ if }0\leq\theta\leq\pi[/latex]. If θ is not in this domain, then we need to find another angle that has the same cosine as θ and does belong to the restricted domain; we then subtract this angle from [latex]\frac{\pi}{2}[/latex]. Similarly, [latex]\sin\theta=\frac{a}{c}=\cos\left(\frac{\pi}{2}−\theta\right)[/latex], so [latex]\cos^{−1}(\sin\theta)=\frac{\pi}{2}−\theta\text{ if }−\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}[/latex]. These are just the function-cofunction relationships presented in another way.

Evaluating Compositions of the Form [latex]f(g^{−1}(x))[/latex]

To evaluate compositions of the form [latex]f(g^{−1}(x))[/latex], where f and g are any two of the functions sine, cosine, or tangent and x is any input in the domain of [latex]g−1[/latex], we have exact formulas, such as [latex]\sin\left({\cos}^{−1}x\right)=\sqrt{1−{x}^{2}}[/latex]. When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, [latex]\sin^{2}x+cos^{2}x=1[/latex], to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.

Example 8: Evaluating the Composition of a Sine with an Inverse Tangent

Find an exact value for [latex]\sin\left(\tan^{−1}\left(\frac{7}{4}\right)\right)[/latex].

Show Solution

While we could use a similar technique as in Example 6, we will demonstrate a different technique here. From the inside, we know there is an angle such that [latex]\tan\theta=\frac{7}{4}[/latex]. We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure 12.

Figure 12. A right triangle with two sides known

Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.

[latex]\begin{gathered}4^{2}+7^{2}=\text{hypotenuse}^{2} \\ \text{hypotenuse}=\sqrt{65} \end{gathered}[/latex]

Key Concepts

• In function composition, if the inside function is an inverse trigonometric function, then there are exact expressions; for example, [latex]\sin\left(\cos^{−1}\left(x\right)\right)=\sqrt{1−x^{2}}[/latex].
• If the inside function is a trigonometric function, then the only possible combinations are [latex]\sin^{−1}\left(\cos x\right)=\frac{\pi}{2}−x[/latex] if [latex]0\leq x\leq\pi[/latex] and [latex]\cos^{−1}\left(\sin x\right)=\frac{\pi}{2}−x[/latex] if [latex]−\frac{\pi}{2}\leq x \leq\frac{\pi}{2}[/latex].
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function.
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides.

Section 7.2 Homework Exercises

For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.

1. [latex]\cos^{−1}(\sin(\pi))[/latex]

2. [latex]\sin^{−1}(\cos(\pi))[/latex]

3. [latex]\tan^{−1}(\sin(\pi))[/latex]

4. [latex]\cos^{−1}\left(\sin\left(\frac{\pi}{3}\right)\right)[/latex]

5. [latex]\tan^{−1}\left(\sin\left(\frac{\pi}{3}\right)\right)[/latex]

6. [latex]\sin^{−1}\left(\cos\left(\frac{−\pi}{2}\right)\right)[/latex]

7. [latex]\tan^{−1}\left(\sin\left(\frac{4\pi}{3}\right)\right)[/latex]

8. [latex]\sin^{−1}\left(\sin\left(\frac{5\pi}{6}\right)\right)[/latex]

9. [latex]\tan^{−1}\left(\sin\left(\frac{−5\pi}{2}\right)\right)[/latex]

10. [latex]\cos\left(\sin^{−1}\left(\frac{4}{5}\right)\right)[/latex]

11. [latex]\sin\left(\cos^{−1}\left(\frac{3}{5}\right)\right)[/latex]

12. [latex]\sin\left(\tan^{−1}\left(\frac{4}{3}\right)\right)[/latex]

13. [latex]\cos\left(\tan^{−1}\left(\frac{12}{5}\right)\right)[/latex]

14. [latex]\cos\left(\sin^{−1}\left(\frac{1}{2}\right)\right)[/latex]

For the following exercises, use a right triangle to write the expression as an algebraic expression.  Assume that x is positive and in the domain of the given inverse trigonometric function.

15. [latex]\tan\left(\sin^{−1}\left(x\right)\right)[/latex]

16. [latex]\sin\left(\cos^{−1}\left(x\right)\right)[/latex]

17. [latex]\cos\left(\sin^{−1}\left(\frac{1}{x}\right)\right)[/latex]

18. [latex]\cos\left(\tan^{−1}\left(3x\right)\right)[/latex]

19. [latex]\sin\left(\tan^{−1}\left(2x\right)\right)[/latex]

20. [latex]\tan\left(\cos^{−1}\left(4x\right)\right)[/latex]