Learning Objectives
- (9.6.1) – Define imaginary and complex numbers
- Express roots of negative numbers in terms of [latex]i[/latex].
- Express imaginary numbers as [latex]bi[/latex] and complex numbers as [latex]a+bi[/latex].
- (9.6.2) – Algebraic operations on complex numbers
- Add and subtract complex numbers
- Multiply and divide complex numbers.
- Simplify powers of [latex]i[/latex]
(9.6.1) – Define imaginary and complex numbers
Up to now, you’ve known it was impossible to take a square root of a negative number. This is true, using only the real numbers. But here you will learn about a new kind of number that lets you work with square roots of negative numbers! Complex numbers are made from both real and imaginary numbers. Imaginary numbers are called imaginary because they are impossible and, therefore, exist only in the world of ideas and pure imagination. Imaginary numbers result from taking the square root of a negative number.
Here we will first define and perform algebraic operations on complex numbers, then we will provide examples of quadratic equations that have solutions that are complex numbers.
Express roots of negative numbers in terms of [latex]i[/latex]
You really need only one new number to start working with the square roots of negative numbers. That number is the square root of [latex]−1,\sqrt{-1}[/latex]. The real numbers are those that can be shown on a number line—they seem pretty real to us! When something’s not real, you often say it is imaginary. So let’s call this new number [latex]i[/latex] and use it to represent the square root of [latex]−1[/latex].
[latex]i=\sqrt{-1}[/latex]
Because [latex]\sqrt{x}\,\cdot \,\sqrt{x}=x[/latex], we can also see that [latex]\sqrt{-1}\,\cdot \,\sqrt{-1}=-1[/latex] or [latex]i\,\cdot \,i=-1[/latex]. We also know that [latex]i\,\cdot \,i={{i}^{2}}[/latex], so we can conclude that [latex]{{i}^{2}}=-1[/latex].
[latex]{{i}^{2}}=-1[/latex]
The number [latex]i[/latex] allows us to work with roots of all negative numbers, not just [latex]\sqrt{-1}[/latex]. There are two important rules to remember: [latex]\sqrt{-1}=i[/latex], and [latex]\sqrt{ab}=\sqrt{a}\sqrt{b}[/latex]. You will use these rules to rewrite the square root of a negative number as the square root of a positive number times [latex]\sqrt{-1}[/latex]. Next you will simplify the square root and rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex]. Let’s try an example.
Example
Simplify. [latex]\sqrt{-4}[/latex]
Example
Simplify. [latex]\sqrt{-18}[/latex]
Example
Simplify. [latex]-\sqrt{-72}[/latex]
You may have wanted to simplify [latex]-\sqrt{-72}[/latex] using different factors. Some may have thought of rewriting this radical as [latex]-\sqrt{-9}\sqrt{8}[/latex], or [latex]-\sqrt{-4}\sqrt{18}[/latex], or [latex]-\sqrt{-6}\sqrt{12}[/latex] for instance. Each of these radicals would have eventually yielded the same answer of [latex]-6i\sqrt{2}[/latex].
In the following video, we show more examples of how to use imaginary numbers to simplify a square root with a negative radicand.
Rewriting the Square Root of a Negative Number
- Find perfect squares within the radical.
- Rewrite the radical using the rule [latex]\sqrt{ab}=\sqrt{a}\cdot \sqrt{b}[/latex].
- Rewrite [latex]\sqrt{-1}[/latex] as [latex]i[/latex].
Example: [latex]\sqrt{-18}=\sqrt{9}\sqrt{-2}=\sqrt{9}\sqrt{2}\sqrt{-1}=3i\sqrt{2}[/latex]
Express imaginary numbers as [latex]bi[/latex] and complex numbers as [latex]a+bi[/latex]
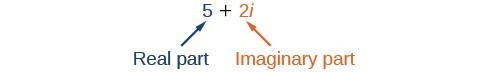
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written [latex]a+bi[/latex] where [latex]a[/latex] is the real part and [latex]bi[/latex] is the imaginary part. For example, [latex]5+2i[/latex] is a complex number. So, too, is [latex]3+4\sqrt{3}i[/latex].
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.
You can use the usual operations (addition, subtraction, multiplication, and so on) with imaginary numbers. You’ll see more of that, later. When you add a real number to an imaginary number, however, you get a complex number. A complex number is any number in the form [latex]a+bi[/latex], where [latex]a[/latex] is a real number and [latex]bi[/latex] is an imaginary number. The number [latex]a[/latex] is sometimes called the real part of the complex number, and [latex]bi[/latex] is sometimes called the imaginary part.
| Complex Number | Real part | Imaginary part |
|---|---|---|
| [latex]3+7i[/latex] | 3 | [latex]7i[/latex] |
| [latex]18–32i[/latex] | 18 | [latex]−32i[/latex] |
| [latex]\displaystyle -\frac{3}{5}+i\sqrt{2}[/latex] | [latex]\displaystyle -\frac{3}{5}[/latex] | [latex]i\sqrt{2}[/latex] |
| [latex]\displaystyle \frac{\sqrt{2}}{2}-\frac{1}{2}i[/latex] | [latex]\displaystyle \frac{\sqrt{2}}{2}[/latex] | [latex]\displaystyle -\frac{1}{2}i[/latex] |
In a number with a radical as part of [latex]b[/latex], such as [latex]\displaystyle -\frac{3}{5}+i\sqrt{2}[/latex] above, the imaginary [latex]i[/latex] should be written in front of the radical. Though writing this number as [latex]\displaystyle -\frac{3}{5}+\sqrt{2}i[/latex] is technically correct, it makes it much more difficult to tell whether [latex]i[/latex] is inside or outside of the radical. Putting it before the radical, as in [latex]\displaystyle -\frac{3}{5}+i\sqrt{2}[/latex], clears up any confusion. Look at these last two examples.
| Number | Number in complex form: [latex]a+bi[/latex] |
Real part | Imaginary part |
|---|---|---|---|
| 17 | [latex]17+0i[/latex] | 17 | [latex]0i[/latex] |
| [latex]−3i[/latex] | [latex]0–3i[/latex] | 0 | [latex]−3i[/latex] |
By making [latex]b=0[/latex], any real number can be expressed as a complex number. The real number [latex]a[/latex] is written [latex]a+0i[/latex] in complex form. Similarly, any imaginary number can be expressed as a complex number. By making [latex]a=0[/latex], any imaginary number [latex]bi[/latex] is written [latex]0+bi[/latex] in complex form.
Example
Write 83.6 as a complex number.
Example
Write [latex]−3i[/latex] as a complex number.
In the next video we show more examples of how to write numbers as complex numbers.
(9.6.2) – Algebraic Operations on Complex Numbers
Add and Subtract Complex Numbers
Any time new kinds of numbers are introduced, one of the first questions that needs to be addressed is, “How do you add them?” In this topic, you’ll learn how to add complex numbers and also how to subtract.
First, consider the following expression.
[latex](6x+8)+(4x+2)[/latex]
To simplify this expression, you combine the like terms, [latex]6x[/latex] and [latex]4x[/latex]. These are like terms because they have the same variable with the same exponents. Similarly, [latex]8[/latex] and [latex]2[/latex] are like terms because they are both constants, with no variables.
[latex](6x+8)+(4x+2)=10x+10[/latex]
In the same way, you can simplify expressions with radicals.
[latex](6\sqrt{3}+8)+(4\sqrt{3}+2)=10\sqrt{3}+10[/latex]
You can add [latex]6\sqrt{3}[/latex] to [latex]4\sqrt{3}[/latex] because the two terms have the same radical, [latex]\sqrt{3}[/latex], just as [latex]6x[/latex] and [latex]4x[/latex] have the same variable and exponent.
The number [latex]i[/latex] looks like a variable, but remember that it is equal to [latex]\sqrt{-1}[/latex]. The great thing is you have no new rules to worry about—whether you treat it as a variable or a radical, the exact same rules apply to adding and subtracting complex numbers. You combine the imaginary parts (the terms with [latex]i[/latex]), and you combine the real parts.
Example
Add. [latex](−3+3i)+(7–2i)[/latex]
Example
Subtract. [latex](−3+3i)–(7–2i)[/latex]
In the following video we show more examples of how to add and subtract complex numbers.
Multiply and Divide Complex Numbers
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Multiplying a Complex Number by a Real Number
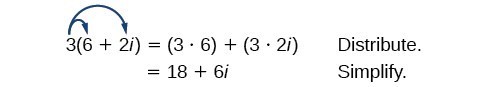
Let’s begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. So,for [latex]3(6+2i)[/latex], 3 is multiplied to both the real and imaginary parts. So we have [latex](3)(6)+(3)(2i) = 18 + 6i[/latex].
How To: Given a complex number and a real number, multiply to find the product.
- Use the distributive property.
- Simplify.
Example
Find the product [latex]4\left(2+5i\right)[/latex].
Multiplying Complex Numbers Together
Now, let’s multiply two complex numbers. We can use either the distributive property or the FOIL method. Recall that FOIL is an acronym for multiplying First, Outer, Inner, and Last terms together. Using either the distributive property or the FOIL method, we get
Because [latex]{i}^{2}=-1[/latex], we have
To simplify, we combine the real parts, and we combine the imaginary parts.
How To: Given two complex numbers, multiply to find the product.
- Use the distributive property or the FOIL method.
- Simplify.
Example
Multiply [latex]\left(4+3i\right)\left(2 - 5i\right)[/latex].
In the first video we show more examples of multiplying complex numbers.
Simplifying Powers of [latex]i[/latex]
The powers of [latex]i[/latex] are cyclic. Let’s look at what happens when we raise [latex]i[/latex] to increasing powers.
We can see that when we get to the fifth power of [latex]i[/latex], it is equal to the first power. As we continue to multiply [latex]i[/latex] by itself for increasing powers, we will see a cycle of 4. Let’s examine the next 4 powers of [latex]i[/latex].
Example
Evaluate [latex]{i}^{35}[/latex].
Q & A
Can we write [latex]{i}^{35}[/latex] in other helpful ways?
As we saw in Example 11, we reduced [latex]{i}^{35}[/latex] to [latex]{i}^{3}[/latex] by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of [latex]{i}^{35}[/latex] may be more useful. The table below shows some other possible factorizations.
| Factorization of [latex]{i}^{35}[/latex] | [latex]{i}^{34}\cdot i[/latex] | [latex]{i}^{33}\cdot {i}^{2}[/latex] | [latex]{i}^{31}\cdot {i}^{4}[/latex] | [latex]{i}^{19}\cdot {i}^{16}[/latex] |
| Reduced form | [latex]{\left({i}^{2}\right)}^{17}\cdot i[/latex] | [latex]{i}^{33}\cdot \left(-1\right)[/latex] | [latex]{i}^{31}\cdot 1[/latex] | [latex]{i}^{19}\cdot {\left({i}^{4}\right)}^{4}[/latex] |
| Simplified form | [latex]{\left(-1\right)}^{17}\cdot i[/latex] | [latex]-{i}^{33}[/latex] | [latex]{i}^{31}[/latex] | [latex]{i}^{19}[/latex] |
Each of these will eventually result in the answer we obtained above but may require several more steps than our earlier method.
In the following video you will see more examples of how to simplify powers of [latex]i[/latex].
Dividing Complex Numbers
Division of two complex numbers is more complicated than addition, subtraction, and multiplication because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator. This idea is similar to rationalizing the denominator of a fraction that contains a radical. To eliminate the complex or imaginary number in the denominator, you multiply by the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. In other words, the complex conjugate of [latex]a+bi[/latex] is [latex]a-bi[/latex].
Note that complex conjugates have a reciprocal relationship: The complex conjugate of [latex]a+bi[/latex] is [latex]a-bi[/latex], and the complex conjugate of [latex]a-bi[/latex] is [latex]a+bi[/latex]. Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another.
Suppose we want to divide [latex]c+di[/latex] by [latex]a+bi[/latex], where neither [latex]a[/latex] nor [latex]b[/latex] equals zero. We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.
Multiply the numerator and denominator by the complex conjugate of the denominator.
Apply the distributive property.
Simplify, remembering that [latex]{i}^{2}=-1[/latex].
A General Note: The Complex Conjugate
The complex conjugate of a complex number [latex]a+bi[/latex] is [latex]a-bi[/latex]. It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.
- When a complex number is multiplied by its complex conjugate, the result is a real number.
- When a complex number is added to its complex conjugate, the result is a real number.
Example
Find the complex conjugate of each number.
- [latex]2+i\sqrt{5}[/latex]
- [latex]-\frac{1}{2}i[/latex]
In the last video you will see more examples of dividing complex numbers.
How To: Given two complex numbers, divide one by the other.
- Write the division problem as a fraction.
- Determine the complex conjugate of the denominator.
- Multiply the numerator and denominator of the fraction by the complex conjugate of the denominator.
- Simplify.
Example
Divide [latex]\left(2+5i\right)[/latex] by [latex]\left(4-i\right)[/latex].
Candela Citations
- Write Number in the Form of Complex Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/mfoOYdDkuyY. License: CC BY: Attribution
- Simplify Square Roots to Imaginary Numbers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/LSp7yNP6Xxc. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 1: Adding and Subtracting Complex Numbers. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/SGhTjioGqqA. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download fro free at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
- Ex: Raising the imaginary unit i to powers. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/sfP6SmEYHRw. License: CC BY: Attribution
- Ex: Dividing Complex Numbers. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/XBJjbJAwM1c. License: CC BY: Attribution
Although we have seen that we can find the complex conjugate of an imaginary number, in practice we generally find the complex conjugates of only complex numbers with both a real and an imaginary component. To obtain a real number from an imaginary number, we can simply multiply by [latex]i[/latex].