Learning Objectives
- (1.5.1) – Set up a linear equation to solve an application
- Translate words into algebraic expressions and equations
- Solve an application using a formula
- (1.5.2) – Solve distance, rate, and time problems
- (1.5.3) – Solve area and perimeter problems
- (1.5.4) – Rearrange formulas to isolate specific variables
- (1.5.5) – Solve temperature conversion problems
Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus an additional charge if you exceed your data plan; a car rental company charges a daily fee plus an amount per mile driven; Chipotle offers a base price for your burrito plus additional charges for extra toppings, like guacamole and sour cream. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.
(1.5.1) – Set Up a Linear Equation to Solve an Application
To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let use an example of a car rental company. The company charges $0.10/mi in addition to a flat rate. In this case, a known cost, such as $0.10/mi, is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write [latex]0.10x[/latex]. This expression represents a variable cost because it changes according to the number of miles driven.
If a quantity is independent of a variable, we usually just add or subtract it, according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges $0.10/mi plus a daily fee of $50. We can use these quantities to model an equation that can be used to find the daily car rental cost [latex]C[/latex].
Translate words into algebraic expressions and equations
When dealing with real-world applications, there are certain expressions that we can translate directly into math. The table lists some common verbal expressions and their equivalent mathematical expressions.
| Verbal | Translation to Math Operations |
|---|---|
| One number exceeds another by a | [latex]x,\text{ }x+a[/latex] |
| Twice a number | [latex]2x[/latex] |
| One number is a more than another number | [latex]x,\text{ }x+a[/latex] |
| One number is a less than twice another number | [latex]x,2x-a[/latex] |
| The product of a number and a, decreased by b | [latex]ax-b[/latex] |
| The quotient of a number and the number plus a is three times the number | [latex]\frac{x}{x+a}=3x[/latex] |
| The product of three times a number and the number decreased by b is c | [latex]3x\left(x-b\right)=c[/latex] |
How To: Given a real-world problem, model a linear equation to fit it.
- Identify known quantities.
- Assign a variable to represent the unknown quantity.
- If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
- Write an equation interpreting the words as mathematical operations.
- Solve the equation. Be sure the solution can be explained in words, including the units of measure.
Example
Find a linear equation to solve for the following unknown quantities: One number exceeds another number by [latex]17[/latex] and their sum is [latex]31[/latex]. Find the two numbers.
In the following video, we show another example of how to translate an expression in english into a mathematical equation that can then be solved.
In the next example we will write equations that will help us compare cell phone plans.
Example
There are two cell phone companies that offer different packages. Company A charges a monthly service fee of $34 plus $.05/min talk-time. Company B charges a monthly service fee of $40 plus $.04/min talk-time.
- Write a linear equation that models the packages offered by both companies.
- If the average number of minutes used each month is 1,160, which company offers the better plan?
- If the average number of minutes used each month is 420, which company offers the better plan?
- How many minutes of talk-time would yield equal monthly statements from both companies?
The following video shows another example of writing two equations that will allow you to compare two different cell phone plans.
Solve an Application Using a Formula
Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region, [latex]A=LW[/latex]; the perimeter of a rectangle, [latex]P=2L+2W[/latex]; and the volume of a rectangular solid, [latex]V=LWH[/latex]. When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.
(1.5.2) – Solve distance, rate, and time problems
Example
It takes Andrew 30 min to drive to work in the morning. He drives home using the same route, but it takes 10 min longer, and he averages 10 mi/h less than in the morning. How far does Andrew drive to work?
(1.5.3) – Solve area and perimeter problems
In the next example, we will find the lengths of a rectangular field given it’s perimeter and a relationship between it’s side lengths.
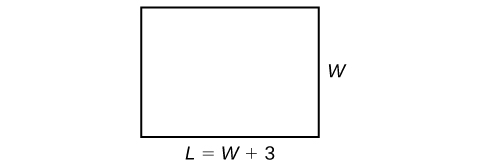
Example
The perimeter of a rectangular outdoor patio is [latex]54[/latex] ft. The length is [latex]3[/latex] ft greater than the width. What are the dimensions of the patio?
The following video shows an example of finding the dimensions of a rectangular field given it’s perimeter.
Example
The perimeter of a tablet of graph paper is 48 in. The length is [latex]6[/latex] in. more than the width. Find the area of the graph paper.
The following video shows another example of finding the area of a rectangle given it’s perimeter and the relationship between it’s side lengths.
(1.5.4) – Rearrange formulas to isolate specific variables
Sometimes, it is easier to isolate the variable you you are solving for when you are using a formula. This is especially helpful if you have to perform the same calculation repeatedly, or you are having a computer perform the calculation repeatedly. In the next examples, we will use algebraic properties to isolate a variable in a formula.
Example
Isolate the term containing the variable, w, from the formula for the perimeter of a rectangle:
[latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex].
Example
Use the multiplication and division properties of equality to isolate the variable b given [latex]A=\frac{1}{2}bh[/latex]
Use the multiplication and division properties of equality to isolate the variable h given [latex]A=\frac{1}{2}bh[/latex]
(1.5.5) – Solve temperature conversion problems
Let’s look at another formula that includes parentheses and fractions, the formula for converting from the Fahrenheit temperature scale to the Celsius scale.
[latex]C=\left(F--32\right)\cdot \frac{5}{9}[/latex]
Example
Given a temperature of [latex]12^{\circ}{C}[/latex], find the equivalent in [latex]{}^{\circ}{F}[/latex].
As with the other formulas we have worked with, we could have isolated the variable F first, then substituted in the given temperature in Celsius.
Example
Solve the formula shown below for converting from the Fahrenheit scale to the Celsius scale for F.
[latex]C=\left(F--32\right)\cdot \frac{5}{9}[/latex]
Candela Citations
- College Algebra. Authored by: Abramson, Jay, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution. License Terms: Download for free at : http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Write and Solve Linear Equation - Number Problem with Given Sum. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/CGC_SwHfwMk. License: CC BY: Attribution
- Write Linear Equations to Model and Compare Cell Phone Plans with Data Usage. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Provided by: https://youtu.be/Q5hlC_VPKGM. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Abramson, Jay, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution. License Terms: Download for free at : http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
- Ex: Find the Dimensions and Area of a Field Given the Perimeter. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/VyK-HQr02iQ. License: CC BY: Attribution
- Ex: Find the Area of a Rectangle Given the Perimeter. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/zUlU64Umnq4. License: CC BY: Attribution
- Find the Volume of a Right Circular Cylinder Formed from a Given Rectangle. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/KS1pGO_g3vM. License: CC BY: Attribution