Learning Objectives
- (6.4.1) – Define solutions to a linear inequality in two variables
- (6.4.2) – Graphing the solution set to a linear inequality in two variables
- (6.4.3) – Graph a system of linear inequalities and define the solutions region
- (6.4.4) – Determine whether a point is a solution to a system of inequalities
- (6.4.5) – Identify when a system of inequalities has no solution
- (6.4.6) – Applications of systems of linear inequalities
(6.4.1) – Define solutions to a linear inequality in two variables
Previously we learned to solve inequalities with only one variable. We will now learn about inequalities containing two variables. In particular we will look at linear inequalities in two variables which are very similar to linear equations in two variables.
Linear inequalities in two variables have many applications. If you ran a business, for example, you would want your revenue to be greater than your costs—so that your business made a profit.
Linear Inequality in Two Variables
A linear inequality in two variables is an inequality that can be written in one of the following forms:
[latex]Ax+By < 0[/latex] [latex]Ax+By>0[/latex] [latex]Ax+By \leq 0[/latex] [latex]Ax+By \geq 0[/latex]
where [latex]A[/latex] and [latex]B[/latex] are not both zero.
Recall that an inequality with one variable had many solutions. For example, the solution to the inequality [latex]x > 3[/latex] is any number greater than 3. We showed this on the number line by shading in the number line to the right of 3, and putting an open parenthesis at 3.
Similarly, linear inequalities in two variables have many solutions. Any ordered pair [latex](x,y)[/latex] that makes an inequality true when we substitute in the values is a solution to a linear inequality.
Solution to a linear inequality in two variables
An ordered pair [latex](x,y)[/latex] is a solution to a linear inequality if the inequality is true when we substitute the values of [latex]x[/latex] and [latex]y[/latex].
ExAMPLE
Determine whether each ordered pair is a solution to the inequality [latex]y>x+4[/latex].
a)[latex](0,0)[/latex]
b)[latex](1,6)[/latex]
Solution Sets of Inequalities
The graph below shows the region of values that makes the inequality [latex]3x+2y\leq6[/latex] true (shaded red), the boundary line [latex]3x+2y=6[/latex], as well as a handful of ordered pairs. The boundary line is solid because points on the boundary line [latex]3x+2y=6[/latex] will make the inequality [latex]3x+2y\leq6[/latex] true.
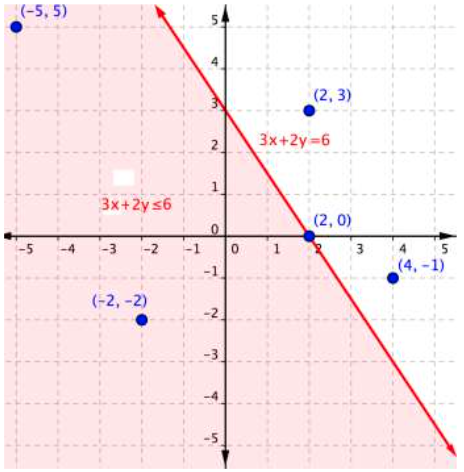
You can substitute the [latex]x[/latex]– and [latex]y[/latex]–values in each of the [latex](x,y)[/latex] ordered pairs into the inequality to find solutions. Sometimes making a table of values makes sense for more complicated inequalities.
| Ordered Pair | Makes the inequality
[latex]3x+2y\leq6[/latex] a true statement |
Makes the inequality
[latex]3x+2y\leq6[/latex] a false statement |
|---|---|---|
| [latex](−5, 5)[/latex] | [latex]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array}[/latex] | |
| [latex](−2,−2)[/latex] | [latex]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\–10\leq6\end{array}[/latex] | |
| [latex](2,3)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/latex] | |
| [latex](2,0)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/latex] | |
| [latex](4,−1)[/latex] | [latex]\begin{array}{r}3\left(4\right)+2\left(−1\right)\leq6\\12+\left(−2\right)\leq6\\10\leq6\end{array}[/latex] |
If substituting [latex](x,y)[/latex] into the inequality yields a true statement, then the ordered pair is a solution to the inequality, and the point will be plotted within the shaded region or the point will be part of a solid boundary line. A false statement means that the ordered pair is not a solution, and the point will graph outside the shaded region, or the point will be part of a dotted boundary line.
Example
Use the graph to determine which ordered pairs plotted below are solutions of the inequality [latex]x–y<3[/latex].
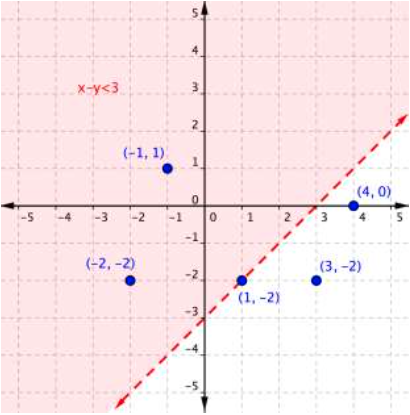
The following video show an example of determining whether an ordered pair is a solution to an inequality.
Example
Is [latex](2,−3)[/latex] a solution of the inequality [latex]y<−3x+1[/latex]?
The following video shows another example of determining whether an ordered pair is a solution to an inequality.
(6.4.2) – Graphing the solution set to a linear inequality in two variables
So how do you get from the algebraic form of an inequality, like [latex]y>3x+1[/latex], to a graph of that inequality? Plotting inequalities is fairly straightforward if you follow a couple steps.
Graphing Inequalities
To graph an inequality:
- Graph the related boundary line. Replace the <, >, ≤ or ≥ sign in the inequality with = to find the equation of the boundary line.
- Identify at least one ordered pair on either side of the boundary line and substitute those [latex](x,y)[/latex] values into the inequality. Shade the region that contains the ordered pairs that make the inequality a true statement.
- If points on the boundary line are solutions, then use a solid line for drawing the boundary line. This will happen for ≤ or ≥ inequalities.
- If points on the boundary line aren’t solutions, then use a dotted line for the boundary line. This will happen for < or > inequalities.
Let’s graph the inequality [latex]x+4y\leq4[/latex].
To graph the boundary line, find at least two values that lie on the line [latex]x+4y=4[/latex]. You can use the x– and y-intercepts for this equation by substituting 0 in for x first and finding the value of y; then substitute 0 in for y and find x.
| x | y |
| 0 | 1 |
| 4 | 0 |
Plot the points [latex](0,1)[/latex] and [latex](4,0)[/latex], and draw a line through these two points for the boundary line. The line is solid because ≤ means “less than or equal to,” so all ordered pairs along the line are included in the solution set.
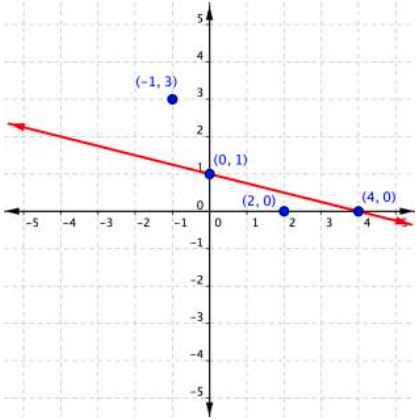
The next step is to find the region that contains the solutions. Is it above or below the boundary line? To identify the region where the inequality holds true, you can test a couple of ordered pairs, one on each side of the boundary line.
If you substitute [latex](−1,3)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}−1+4\left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]
This is a false statement, since 11 is not less than or equal to 4.
On the other hand, if you substitute [latex](2,0)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}2+4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{array}[/latex]
This is true! The region that includes [latex](2,0)[/latex] should be shaded, as this is the region of solutions.
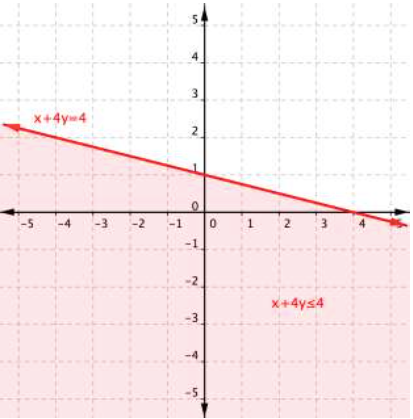
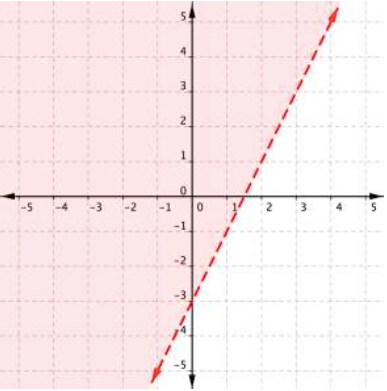
And there you have it—the graph of the set of solutions for [latex]x+4y\leq4[/latex].
Example
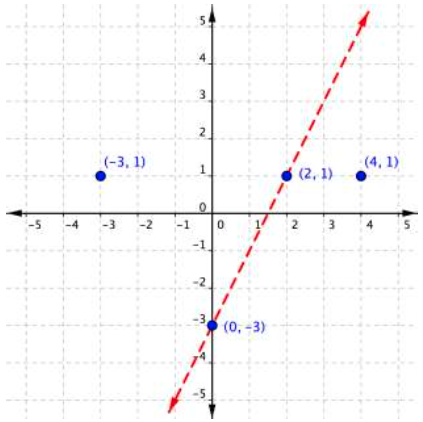
Graph the inequality [latex]2y>4x–6[/latex].
A quick note about the problem above—notice that you can use the points [latex](0,−3)[/latex] and [latex](2,1)[/latex] to graph the boundary line, but that these points are not included in the region of solutions, since the region does not include the boundary line!
(6.4.3) – Graph a system of linear inequalities and define the solutions region
Consider the graph of the inequality [latex]y<2x+5[/latex].
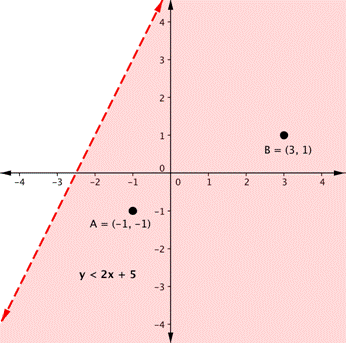
The dashed line is [latex]y=2x+5[/latex]. Every ordered pair in the shaded area below the line is a solution to [latex]y<2x+5[/latex], as all of the points below the line will make the inequality true. If you doubt that, try substituting the [latex]x[/latex] and [latex]y[/latex] coordinates of Points A and B into the inequality—you’ll see that they work. So, the shaded area shows all of the solutions for this inequality.
The boundary line divides the coordinate plane in half. In this case, it is shown as a dashed line as the points on the line don’t satisfy the inequality. If the inequality had been [latex]y\leq2x+5[/latex], then the boundary line would have been solid.
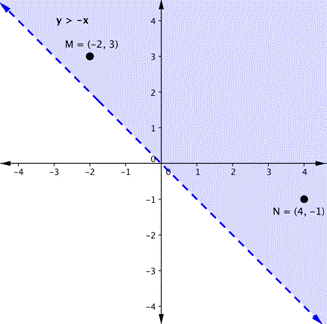
Let’s graph another inequality: [latex]y>−x[/latex]. You can check a couple of points to determine which side of the boundary line to shade. Checking points M and N yield true statements. So, we shade the area above the line. The line is dashed as points on the line are not true.
To create a system of inequalities, you need to graph two or more inequalities together. Let’s use [latex]y<2x+5[/latex] and [latex]y>−x[/latex] since we have already graphed each of them.
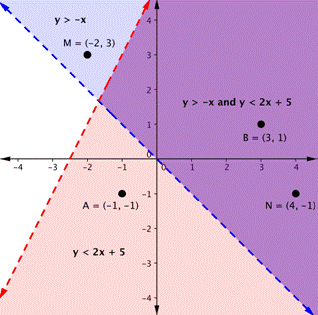
The purple area shows where the solutions of the two inequalities overlap. This area is the solution to the system of inequalities. Any point within this purple region will be true for both [latex]y>−x[/latex] and [latex]y<2x+5[/latex].
In the following video examples, we show how to graph a system of linear inequalities, and define the solution region.
In the next section, we will see that points can be solutions to systems of equations and inequalities. We will verify algebraically whether a point is a solution to a linear equation or inequality.
(6.4.4) – Determine whether a point is a solution to a system of inequalities
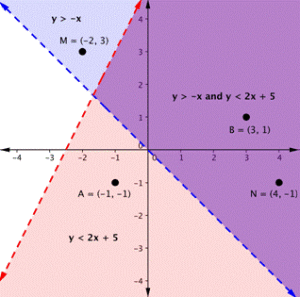
On the graph above, you can see that the points B and N are solutions for the system because their coordinates will make both inequalities true statements.
In contrast, points M and A both lie outside the solution region (purple). While point M is a solution for the inequality [latex]y>−x[/latex] and point A is a solution for the inequality [latex]y<2x+5[/latex], neither point is a solution for the system. The following example shows how to test a point to see whether it is a solution to a system of inequalities.
Example
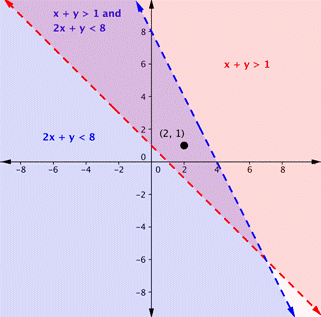
Is the point [latex](2,1)[/latex] a solution of the system [latex]x+y>1[/latex] and [latex]2x+y<8[/latex]?
Here is a graph of the system in the example above. Notice that [latex](2,1)[/latex] lies in the purple area, which is the overlapping area for the two inequalities.
Example
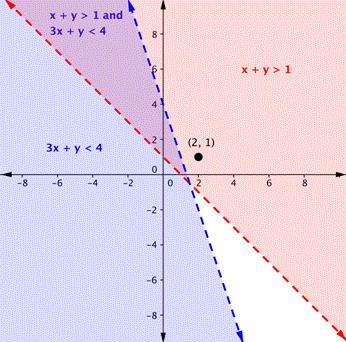
Is the point [latex](2,1)[/latex] a solution of the system [latex]x+y>1[/latex] and [latex]3x+y<4[/latex]?
Here is a graph of this system. Notice that [latex](2, 1)[/latex] is not in the purple area, which is the overlapping area; it is a solution for one inequality (the red region), but it is not a solution for the second inequality (the blue region).
In the following video we show another example of determining whether a point is in the solution of a system of linear inequalities.
As shown above, finding the solutions of a system of inequalities can be done by graphing each inequality and identifying the region they share. Below, you are given more examples that show the entire process of defining the region of solutions on a graph for a system of two linear inequalities. The general steps are outlined below:
- Graph each inequality as a line and determine whether it will be solid or dashed
- Determine which side of each boundary line represents solutions to the inequality by testing a point on each side
- Shade the region that represents solutions for both inequalities
(6.4.5) – Identify when a system of inequalities has no solution
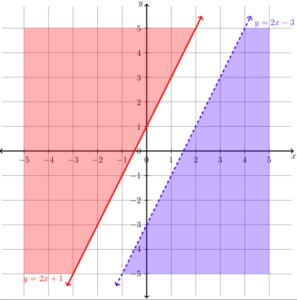
In the next example, we will show the solution to a system of two inequalities whose boundary lines are parallel to each other. When the graphs of a system of two linear equations are parallel to each other, we found that there was no solution to the system. We will get a similar result for the following system of linear inequalities.
Examples
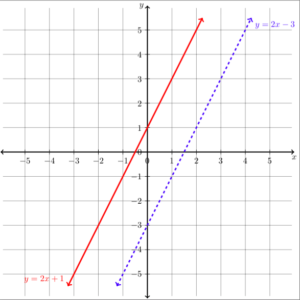
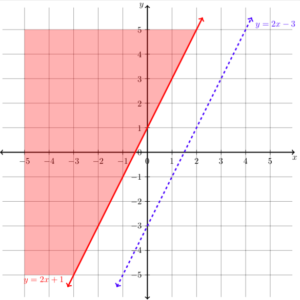
Graph the system [latex]\begin{array}{c}y\ge2x+1\\y\lt2x-3\end{array}[/latex]
In the following examples, we will continue to practice graphing the solution region for systems of linear inequalities. We will also graph the solutions to a system that includes a compound inequality.
Example
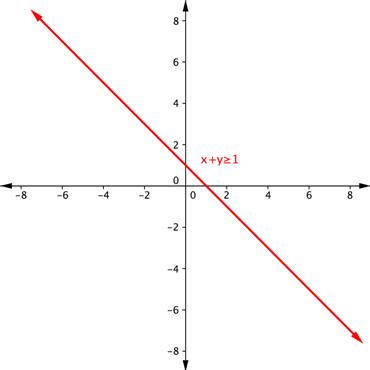
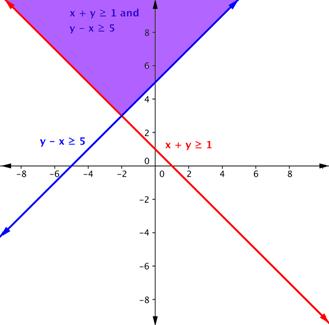
Shade the region of the graph that represents solutions for both inequalities. [latex]x+y\geq 1[/latex] and [latex]y -x\geq 5[/latex].
The videos that follow show more examples of graphing the solution set of a system of linear inequalities.
The system in our last example includes a compound inequality. We will see that you can treat a compound inequality like two lines when you are graphing them.
Example
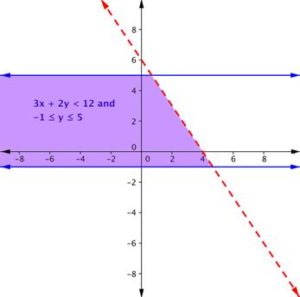
Find the solution to the system [latex]3x + 2y < 12[/latex] and [latex]−1\leq y \leq 5[/latex].
In the video that follows, we show how to solve another system of inequalities.
(6.4.6) – Applications of systems of linear inequalities
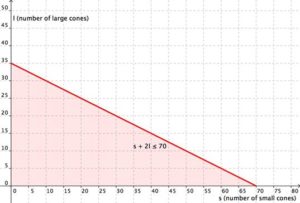
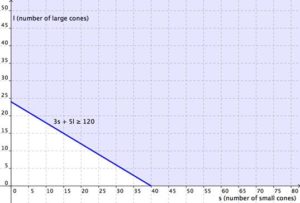
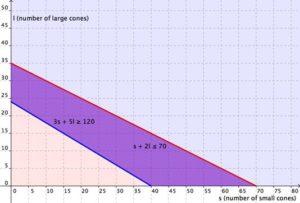
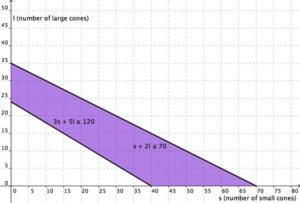
In our first example we will show how to write and graph a system of linear inequalities that models the amount of sales needed to obtain a specific amount of money.
Example
Cathy is selling ice cream cones at a school fundraiser. She is selling two sizes: small (which has 1 scoop) and large (which has 2 scoops). She knows that she can get a maximum of 70 scoops of ice cream out of her supply. She charges $3 for a small cone and $5 for a large cone.
Cathy wants to earn at least $120 to give back to the school. Write and graph a system of inequalities that models this situation.
In a previous example for finding a solution to a system of linear equations, we introduced a manufacturer’s cost and revenue equations:
Cost: [latex]y=0.85x+35,000[/latex]
Revenue: [latex]y=1.55x[/latex]
The cost equation is shown in blue in the graph below, and the revenue equation is graphed in orange.The point at which the two lines intersect is called the break-even point, we learned that this is the solution to the system of linear equations that in this case comprise the cost and revenue equations.
The shaded region to the right of the break-even point represents quantities for which the company makes a profit. The region to the left represents quantities for which the company suffers a loss.
In the next example, you will see how the information you learned about systems of linear inequalities can be applied to answering questions about cost and revenue.
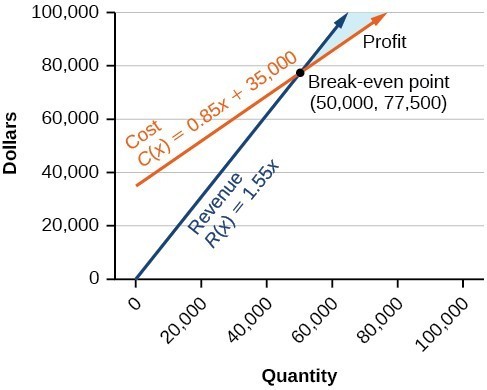
Note how the blue shaded region between the Cost and Revenue equations is labeled Profit. This is the “sweet spot” that the company wants to achieve where they produce enough bike frames at a minimal enough cost to make money. They don’t want more money going out than coming in!
Example
Define the profit region for the skateboard manufacturing business using inequalities, given the system of linear equations:
Cost: [latex]y=0.85x+35,000[/latex]
Revenue: [latex]y=1.55x[/latex]
In the following video you will see an example of how to find the break even point for a small sno-cone business.
And here is one more video example of solving an application using a sustem of linear inequalities.
We have seen that systems of linear equations and inequalities can help to define market behaviors that are very helpful to businesses. The intersection of cost and revenue equations gives the break even point, and also helps define the region for which a company will make a profit.