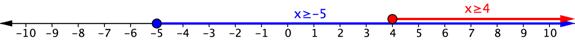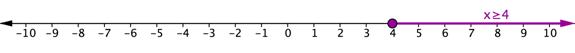(6.2.1) – Use interval notation to describe sets of numbers as intersections and unions

When two inequalities are joined by the word and, the solution of the simple compound inequality occurs when both inequalities are true at the same time. It is the overlap, or intersection, of the solutions for each inequality. When the two inequalities are joined by the word or, the solution of the compound inequality occurs when either of the inequalities is true. The solution is the combination, or union, of the two individual solutions.

In this section we will learn how to solve simple compound inequalities that are joined with the words AND and OR. First, it will help to see some examples of inequalities, intervals, and graphs of compound inequalities. This will help you describe the solutions to compound inequalities properly.

Venn diagrams use the concept of intersections and unions to show how much two or more things share in common. For example, this Venn diagram shows the intersection of people who are breaking your heart and those who are shaking your confidence daily. Apparently Cecilia has both of these qualities; therefore she is the intersection of the two.

In mathematical terms, consider the inequality [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. How would we interpret what numbers x can be, and what would the interval look like?

In words, x must be less than 6 and at the same time, it must be greater than 2, much like the Venn diagram above, where Cecilia is at once breaking your heart and shaking your confidence daily. Let’s look at a graph to see what numbers are possible with these constraints.

The numbers that are shared by both lines on the graph are called the intersection of the two inequalities [latex]x\lt6[/latex] and [latex]x\gt2[/latex]. This is called a bounded inequality and is written as [latex]2\lt{x}\lt6[/latex]. Think about that one for a minute. [latex]x[/latex] must be less than 6 and greater than two—the values for [latex]x[/latex] will fall between two numbers. In interval notation, this looks like [latex]\left(2,6\right)[/latex]. The graph would look like this:

On the other hand, if you need to represent two things that don’t share any common elements or traits, you can use a union. The following Venn diagram shows two things that share no similar traits or elements but are often considered in the same application, such as online shopping or banking.

In mathematical terms, for example, [latex]x>6[/latex] or [latex]x<2[/latex] is an inequality joined by the word or. Using interval notation, we can describe each of these inequalities separately:

[latex]x\gt6[/latex] is the same as [latex]\left(6, \infty\right)[/latex] and [latex]x<2[/latex] is the same as [latex]\left(\infty, 2\right)[/latex]. If we are describing solutions to inequalities, what effect does the or have?  We are saying that solutions are either real numbers less than two or real numbers greater than 6. Can you see why we need to write them as two separate intervals? Let’s look at a graph to get a clear picture of what is going on.

When you place both of these inequalities on a graph, we can see that they share no numbers in common. This is what we call a union, as mentioned above. The interval notation associated with a union is a big U, so instead of writing or, we join our intervals with a big U, like this:

[latex]\left(\infty, 2\right)\cup\left(6, \infty\right)[/latex]

It is common convention to construct intervals starting with the value that is furthest left on the number line as the left value, such as [latex]\left(2,6\right)[/latex], where 2 is less than 6. The number on the right should be greater than the number on the left.

Example

Draw the graph of the simple compound inequality [latex]x\gt3[/latex] or [latex]x\le4[/latex] and describe the set of x-values that will satisfy it with an interval.

Note, in interval notation, you are asked to find [latex](-\infty,4] \cup (3,\infty)[/latex].

Show Solution

The graph of [latex]x\gt3[/latex] has an open circle on 3 and a blue arrow drawn to the right to contain all the numbers greater than 3.

The graph of [latex]x\le4[/latex] has a closed circle at 4 and a red arrow to the left to contain all the numbers less than 4.

What do you notice about the graph that combines these two inequalities?

Since this compound inequality is an or statement, it includes all of the numbers in each of the solutions. In this case, the solution is all the numbers on the number line. (The region of the line greater than 3 and less than or equal to 4 is shown in purple because it lies on both of the original graphs.) The solution to the compound inequality [latex]x\gt3[/latex] or [latex]x\le4[/latex] is the set of all real numbers, and can be described in interval notation as [latex]\left(-\infty, \infty\right)[/latex].

As a result we have: [latex](-\infty,4] \cup (3,\infty)=(-\infty,\infty)[/latex].

In the following video you will see two examples of how to express inequalities involving OR graphically and as an interval.

Examples

Draw a graph of the simple compound inequality: [latex]x\lt5[/latex] and [latex]x\ge−1[/latex], and describe the set of [latex]x[/latex]-values that will satisfy it with an interval.

Note, in interval notation, you are asked to find [latex](-\infty,5) \cap [-1,\infty)[/latex].

Show Solution

The graph of each individual inequality is shown in color.

Since the word and joins the two inequalities, the solution is the overlap of the two solutions. This is where both of these statements are true at the same time.

The solution to this compound inequality is shown below.

Notice that this is a bounded inequality. You can rewrite [latex]x\ge−1\,\text{and }x\le5[/latex] as [latex]−1\le x\le 5[/latex] since the solution is between [latex]−1[/latex] and 5, including [latex]−1[/latex]. You read [latex]−1\le x\lt{5}[/latex] as “[latex]x[/latex] is greater than or equal to [latex]−1[/latex] and less than 5.” You can rewrite an and statement this way only if the answer is between two numbers. The set of solutions to this inequality can be written in interval notation like this: [latex]\left[{-1},{5}\right)[/latex]

As a result we have: [latex](-\infty,5)) \cap [-1,\infty)=[-1,5)[/latex].

Examples

Draw the graph of the simple compound inequality [latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex], and describe the set of [latex]x[/latex]-values that will satisfy it with an interval.

Note, in interval notation, you are asked to find [latex](-\infty,-3) \cap (3,\infty)[/latex].

Show Solution

First, draw a graph. We are looking for values for x that will satisfy both inequalities since they are joined with the word and.

In this case, there are no shared x-values, and therefore there is no intersection for these two inequalities. We can write “no solution,” or DNE.

As a result we have: [latex](-\infty,-3) \cap (3,\infty) = \varnothing[/latex] (DNE).

The following video presents two examples of how to draw inequalities involving AND, as well as write the corresponding intervals.

(6.2.2) – Solve compound inequalities—OR

As we saw in the last section, the solution of a simple compound inequality that consists of two inequalities joined with the word or is the union of the solutions of each inequality. Unions allow us to create a new set from two that may or may not have elements in common.

In this section you will see that some inequalities need to be simplified before their solution can be written or graphed.

In the following example, you will see an example of how to solve a one-step inequality in the OR form. Note how each inequality is treated independently until the end where the solution is described in terms of both inequalities. You will use the same properties to solve compound inequalities that you used to solve regular inequalities.

Example

Solve for [latex]x[/latex].  [latex]3x–1<8[/latex] or [latex]x–5>0[/latex]

Show Solution

Solve each inequality by isolating the variable.

[latex] \displaystyle \begin{array}{r}x-5>0\,\,\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,\,\,\,\,3x-1<8\\\underline{\,\,\,+5\,\,+5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,+1\,+1}\\x\,\,\,\,\,\,>5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{3x}\,\,\,<\underline{9}\\{3}\,\,\,\,\,\,\,\,\,\,\,\,\,{3}\\x<3\,\,\,\\x>5\,\,\,\,\text{or}\,\,\,\,x<3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Write both inequality solutions as a compound using or, using interval notation.

Answer

Inequality: [latex] \displaystyle x>5\,\,\,\,\text{or}\,\,\,\,x<3[/latex]

Interval: [latex]\left(-\infty, 3\right)\cup\left(5,\infty\right)[/latex]

The solution to this compound inequality can also be shown graphically. Sometimes it helps to draw the graph first before writing the solution using interval notation.

Remember to apply the properties of inequality when you are solving compound inequalities. The next example involves dividing by a negative to isolate a variable.

Example

Solve for [latex]y[/latex].  [latex]2y+7\lt13\text{ or }−3y–2\lt10[/latex]

Show Solution

Solve each inequality separately.

[latex] \displaystyle \begin{array}{l}2y+7<13\,\,\,\,\,\,\,\,\,\text{OR}\,\,\,\,\,\,\,-3y-2\le 10\\\underline{\,\,\,\,\,\,\,-7\,\,\,\,-7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,+2\,\,\,\,\,+2}\\\frac{2y}{2}\,\,\,\,\,\,\,\,<\,\,\,\frac{6}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{-3y}{-3}\,\,\,\,\,\,\,\,\ge \frac{12}{-3}\\\,\,\,\,\,\,\,\,\,\,y<3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y\ge -4\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,y<3\,\,\,\,\text{or}\,\,\,\,y\ge -4\end{array}[/latex]

The inequality sign is reversed with division by a negative number.

Since y could be less than 3 or greater than or equal to [latex]−4[/latex], y could be any number. Graphing the inequality helps with this interpretation.

Answer

Inequality: [latex]y<3\text{ or }y\ge -4[/latex]

Interval: [latex]\left(-\infty,\infty\right)[/latex]

Graph:

In the last example, the final answer included solutions whose intervals overlapped, causing the answer to include all the numbers on the number line. In words, we call this solution “all real numbers.”  Any real number will produce a true statement for either [latex]y<3\text{ or }y\ge -4[/latex], when it is substituted for x.

The following video contains an example of solving a compound inequality involving OR, and drawing the associated graph.

In the next section you will see examples of how to solve compound inequalities containing and.

(6.2.3) – Solve compound inequalities—AND

The solution of a compound inequality that consists of two inequalities joined with the word and is the intersection of the solutions of each inequality. In other words, both statements must be true at the same time. The solution to an and compound inequality are all the solutions that the two inequalities have in common. As we saw in the last sections, this is where the two graphs overlap.

In this section we will see more examples where we have to simplify the compound inequalities before we can express their solutions graphically or with an interval.

Example

Solve for x. [latex] \displaystyle 1-4x\le 21\,\,\,\,\text{and}\,\,\,\,5x+2\ge22[/latex]

Show Solution

Solve each inequality for x. Determine the intersection of the solutions.

[latex] \displaystyle \begin{array}{r}\,\,\,1-4x\le 21\,\,\,\,\,\,\,\,\text{AND}\,\,\,\,\,\,\,5x+2\ge 22\\\underline{-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-2\,\,\,\,-2}\\\,\,\,\,\,\underline{-4x}\leq \underline{20}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{5x}\,\,\,\,\,\,\,\ge \underline{20}\\\,\,\,\,\,{-4}\,\,\,\,\,\,\,{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{5}\,\,\\\,\,\,\,\,\,\,\,\,\,\,x\ge -5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\ge 4\,\,\,\,\\\\x\ge -5\,\text{and}\,\,x\ge 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

The number line below shows the graphs of the two inequalities in the problem. The solution to the compound inequality is [latex]x\geq4[/latex], since this is where the two graphs overlap.

Answer

Inequality: [latex] \displaystyle x\ge 4[/latex]

Interval: [latex]\left[4,\infty\right)[/latex]

Graph:

Compound inequalities in the form [latex]a<x<b[/latex]

Rather than splitting a compound inequality in the form of  [latex]a<x<b[/latex] into two inequalities [latex]x<b[/latex] and [latex]x>a[/latex], you can more quickly to solve the inequality by applying the properties of inequality to all three segments of the compound inequality.

Example

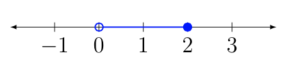
Solve for [latex]x[/latex]. [latex]3\lt2x+3\leq 7[/latex]

Show Solution

Isolate the variable by subtracting 3 from all 3 parts of the inequality, then dividing each part by 2.

[latex]\begin{array}{r}\,\,\,\,3\,\,\lt\,\,2x+3\,\,\leq \,\,\,\,7\\\underline{\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\underline{\,-3}\,\\\,\,\,\,\,\underline{\,0\,}\,\,\lt\,\,\,\,\underline{2x}\,\,\,\,\,\,\,\,\leq\,\,\,\underline{\,4\,}\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\\\,\,\,\,\,\,\,\,\,\,0\lt x\leq 2\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Answer

Inequality: [latex] \displaystyle 0\lt{x}\le 2[/latex]

Interval: [latex]\left(0,2\right][/latex]

Graph:

In the video below, you will see another example of how to solve an inequality in the form  [latex]a<x<b[/latex]

Solution

Lets try the first method. Write two inequalities:

[latex]\begin{array}{lll}3+x> 7x - 2\hfill & \text{and}\hfill & 7x - 2> 5x - 10\hfill \\ 3> 6x - 2\hfill & \hfill & 2x - 2> -10\hfill \\ 5> 6x\hfill & \hfill & 2x> -8\hfill \\ \frac{5}{6}> x\hfill & \hfill & x> -4\hfill \\ x< \frac{5}{6}\hfill & \hfill & -4< x\hfill \end{array}[/latex]

The solution set is [latex]-4<x<\frac{5}{6}[/latex] or in interval notation [latex]\left(-4,\frac{5}{6}\right)[/latex]. Notice that when we write the solution in interval notation, the smaller number comes first. We read intervals from left to right, as they appear on a number line.

Figure 3

To solve inequalities like [latex]a<x<b[/latex], use the addition and multiplication properties of inequality to solve the inequality for [latex]x[/latex]. Whatever operation you perform on the middle portion of the inequality, you must also perform to each of the outside sections as well. Pay particular attention to division or multiplication by a negative.

The solution to a compound inequality with and is always the overlap between the solution to each inequality. There are three possible outcomes for compound inequalities joined by the word and:

Case 1:
Description	The solution could be all the values between two endpoints
Inequalities	[latex]x\le{1}[/latex] and [latex]x\gt{-1}[/latex], or as a bounded inequality: [latex]{-1}\lt{x}\le{1}[/latex]
Interval	[latex](-\infty,1] \cap (-1,\infty) = \left(-1,1\right][/latex]
Graphs
Case 2:
Description	The solution could begin at a point on the number line and extend in one direction.
Inequalities	[latex]x\gt3[/latex] and [latex]x\ge4[/latex]
Interval	[latex](-3,\infty) \cap [4,\infty) = \left[4,\infty\right)[/latex]
Graphs
Case 3:
Description	In cases where there is no overlap between the two inequalities, there is no solution to the compound inequality
Inequalities	[latex]x\lt{-3}[/latex] and [latex]x\gt{3}[/latex]
Intervals	[latex]\left(-\infty,-3\right) \cap \left(3,\infty\right) = \varnothing[/latex] (DNE)
Graph

In the example below, there is no solution to the compound inequality because there is no overlap between the inequalities.

Example

Solve for [latex]x[/latex]. [latex]x+2>5[/latex] and [latex]x+4<5[/latex]

Show Solution

Solve each inequality separately.

[latex] \displaystyle \begin{array}{l}x+2>5\,\,\,\,\,\,\,\,\,\text{AND}\,\,\,\,\,\,\,x+4<5\,\,\,\,\\\underline{\,\,\,\,\,-2\,-2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-4\,-4}\\x\,\,\,\,\,\,\,\,>\,\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,<\,1\\\\\,\,\,\,\,\,\,\,\,\,\,\,\,x>3\,\,\,\,\text{and}\,\,\,\,x<1\end{array}[/latex]

Find the overlap between the solutions.

Answer

There is no overlap between [latex] \displaystyle x>3[/latex] and [latex]x<1[/latex], so there is no solution.