(8.1.1) – Recognize and define a rational expression

Rational expressions are fractions that have a polynomial in the numerator, denominator, or both. Although rational expressions can seem complicated because they contain variables, they can be simplified using the techniques used to simplify expressions such as [latex]\displaystyle \frac{4x^3}{12x^2}[/latex] combined with techniques for factoring polynomials. There are a couple ways to get yourself into trouble when working with rational expressions, equations and functions.  One of them is dividing by zero, and the other is trying to divide across addition or subtraction.

Determine the domain of a rational expression

One sure way you can break math is to divide by zero. Consider the following rational expression evaluated at x = 2:

Evaluate  [latex]\displaystyle \frac{x}{x-2}[/latex] for [latex]x=2[/latex]

Substitute [latex]x=2[/latex]

[latex]\large \begin{array}{l}\frac{2}{2-2}\\\text{}\\=\frac{2}{0}\end{array}[/latex]

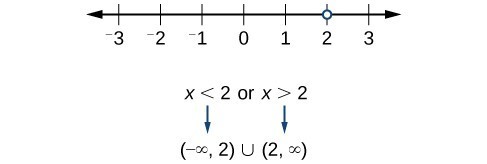
This means that for the expression [latex]\displaystyle \frac{x}{x-2}[/latex], [latex]x[/latex] cannot be 2 because it will result in an undefined ratio. In general, finding values for a variable that will not result in division by zero is called finding the domain. Finding the domain of a rational expression or function will help you not break math.

The reason you cannot divide any number [latex]c[/latex] by zero [latex]\displaystyle \left( \frac{c}{0}\,\,=\,\,? \right)\\[/latex] is that you would have to find a number that when you multiply it by 0 you would get back [latex]c \left( ?\,\,\cdot \,\,0\,\,=\,\,c \right)[/latex]. There are no numbers that can do this, so we say “division by zero is undefined”. In simplifying rational expressions you need to pay attention to what values of the variable(s) in the expression would make the denominator equal zero. These values cannot be included in the domain, so they’re called excluded values. Discard them right at the start, before you go any further.

(Note that although the denominator cannot be equivalent to 0, the numerator can—this is why you only look for excluded values in the denominator of a rational expression.)

For rational expressions, the domain will exclude values for which the value of the denominator is 0. The following example illustrates finding the domain of an expression. Note that this is exactly the same algebra used to find the domain of a function.

(8.1.2) – Simplify Rational Expressions

Before we dive in to simplifying rational expressions, let’s review the difference between a factor,  a term,  and an expression.  This will hopefully help you avoid another way to break math when you are simplifying rational expressions.

Factors are the building blocks of multiplication. They are the numbers that you can multiply together to produce another number: 2 and 10 are factors of 20, as are 4, 5, 1, 20.

Terms are single numbers, or variables and numbers connected by multiplication. [latex]-4[/latex], [latex]6x[/latex] and [latex]x^2[/latex] are all terms.

Expressions are groups of terms connected by addition and subtraction.  [latex]2x^2-5[/latex] is an expression.

This distinction is important when you are required to divide.  Let’s use an example to show why this is important.

Simplify: [latex]\displaystyle \large\frac{2x^2}{12x}[/latex]

The numerator and denominator of this fraction consist of factors. To simplify it, we can divide without being impeded by addition or subtraction.

[latex]\displaystyle \begin{array}{cc}\Large\frac{2x^2}{12x}\\=\Large\frac{2\cdot{x}\cdot{x}}{2\cdot3\cdot2\cdot{x}}\\=\Large\frac{\cancel{2}\cdot{\cancel{x}}\cdot{x}}{\cancel{2}\cdot3\cdot2\cdot{\cancel{x}}}\end{array}[/latex]

We can do this because [latex]\displaystyle \frac{2}{2}=1\text{ and }\frac{x}{x}=1[/latex], so our expression simplifies to [latex]\displaystyle \large\frac{x}{6}[/latex]

Compare that to the expression [latex]\displaystyle \large\frac{2x^2+x}{12-2x}[/latex], notice the denominator and numerator consist of two terms connected by addition and subtraction.  We have to tip-toe around the addition and subtraction.  When asked to simplify it is tempting to want to cancel out like terms as we did when we just had factors. But you can’t do that, it will break math!

Breaking Math

In the examples that follow, the numerator and the denominator are polynomials with more than one term, and we will show you how to properly simplify them by factoring – which turns expressions connected by addition and subtraction into terms connected by multiplication.

We will show one last example of simplifying a rational expression. See if you can recognize the special product in the numerator.

In the following video we present another example of finding the domain of a rational expression.

(8.1.3) – Defining Rational Functions

We started this section stating that a rational expression is an expression of the form [latex]\displaystyle \frac{p}{q} [/latex] where [latex]p[/latex] and  [latex]q[/latex] are polynomials and [latex]q(x) \neq 0.[/latex] Similarly, we define a rational function as a function of the form:

[latex]\displaystyle R(x) = \frac{p(x)}{q(x)}[/latex]

where [latex]p(x)[/latex] and [latex]q(x)[/latex] are polynomial functions and [latex]q(x)[/latex] is not zero.

The domain of a rational function is all real numbers except for those values that would cause division by zero. We must eliminate any values that make  [latex]q(x) = 0[/latex].

For example, [latex]\displaystyle f(x) = \frac{1}{x}[/latex] and [latex]\displaystyle f(x) = \frac{1}{x^2}[/latex] are examples of rational functions.

Finding the domain of rational functions

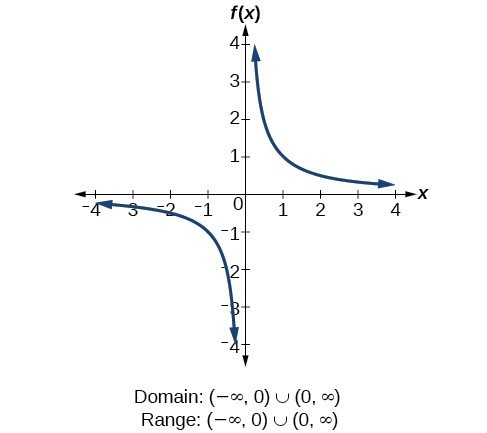
For the rational function [latex]\displaystyle f\left(x\right)=\frac{1}{x}[/latex] (also called the reciprocal function), we cannot divide by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. In set-builder notation, we could also write [latex]\left\{x|\text{ }x\ne 0\right\}[/latex], the set of all real numbers that are not zero.

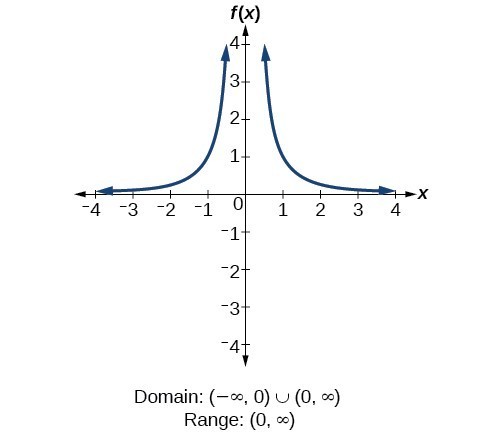
For the rational function [latex]\displaystyle f\left(x\right)=\frac{1}{{x}^{2}}[/latex], we cannot divide by [latex]0[/latex], so we must exclude [latex]0[/latex] from the domain. There is also no [latex]x[/latex] that can give an output of 0, so 0 is excluded from the range as well. Note that the output of this function is always positive due to the square in the denominator, so the range includes only positive numbers.

Example: Finding the Domain of a Rational Function

Find the domain of the function [latex]\displaystyle f\left(x\right)=\frac{x+1}{2-x}[/latex].

Solution

When there is a denominator, we want to include only values of the input that do not force the denominator to be zero. So, we will set the denominator equal to 0 and solve for [latex]x[/latex].

[latex]\begin{cases}2-x=0\hfill \\ -x=-2\hfill \\ x=2\hfill \end{cases}[/latex]

Now, we will exclude 2 from the domain. The answers are all real numbers where [latex]x<2[/latex] or [latex]x>2[/latex]. We can use a symbol known as the union, [latex]\cup [/latex], to combine the two sets. In interval notation, we write the solution: [latex]\left(\mathrm{-\infty },2\right)\cup \left(2,\infty \right)[/latex].

In interval form, the domain of [latex]f[/latex] is [latex]\left(-\infty ,2\right)\cup \left(2,\infty \right)[/latex].