Learning Outcomes
- Find the common difference for an arithmetic sequence
- Find terms of an arithmetic sequence
The values of the truck in the example on the previous page form an arithmetic sequence because they change by a constant amount each year. Each term increases or decreases by the same constant value called the common difference of the sequence. For this sequence the common difference is –3,400.

The sequence below is another example of an arithmetic sequence. In this case the constant difference is 3. You can choose any term of the sequence, and add 3 to find the subsequent term.

A General Note: Arithmetic Sequence
An arithmetic sequence is a sequence that has the property that the difference between any two consecutive terms is a constant. This constant is called the common difference. If [latex]{a}_{1}[/latex] is the first term of an arithmetic sequence and [latex]d[/latex] is the common difference, the sequence will be:
[latex]\left\{{a}_{n}\right\}=\left\{{a}_{1},{a}_{1}+d,{a}_{1}+2d,{a}_{1}+3d,...\right\}[/latex]
Example: Finding Common Differences
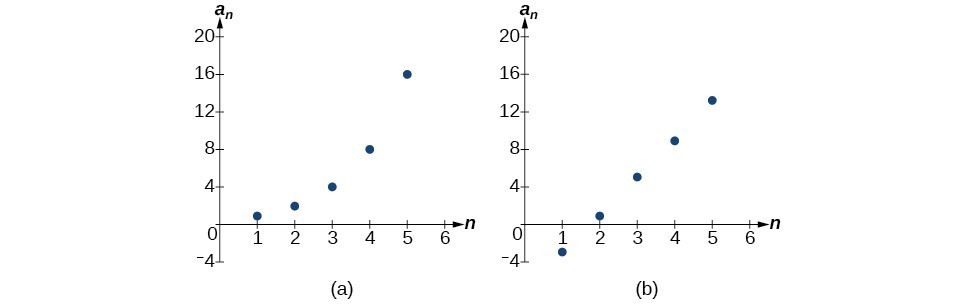
Is each sequence arithmetic? If so, find the common difference.
- [latex]\left\{1,2,4,8,16,...\right\}[/latex]
- [latex]\left\{-3,1,5,9,13,...\right\}[/latex]
Q & A
If we are told that a sequence is arithmetic, do we have to subtract every term from the following term to find the common difference?
No. If we know that the sequence is arithmetic, we can choose any one term in the sequence, and subtract it from the subsequent term to find the common difference.
Try It
Is the given sequence arithmetic? If so, find the common difference.
[latex]\left\{18,16,14,12,10,\dots \right\}[/latex]
Try It
Is the given sequence arithmetic? If so, find the common difference.
[latex]\left\{1,3,6,10,15,\dots \right\}[/latex]
Writing Terms of Arithmetic Sequences
Now that we can recognize an arithmetic sequence, we will find the terms if we are given the first term and the common difference. The terms can be found by beginning with the first term and adding the common difference repeatedly. In addition, any term can also be found by plugging in the values of [latex]n[/latex] and [latex]d[/latex] into formula below.
[latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex]
tip for success
The formula given above is a handy tool for calculating any term of an arithmetic sequence. As you work to memorize it, do work out the terms in the examples below individually as well to build you intuition for why the formula works.
How To: Given the first term and the common difference of an arithmetic sequence, find the first several terms.
- Add the common difference to the first term to find the second term.
- Add the common difference to the second term to find the third term.
- Continue until all of the desired terms are identified.
- Write the terms separated by commas within brackets.
Example: Writing Terms of Arithmetic Sequences
Write the first five terms of the arithmetic sequence with [latex]{a}_{1}=17[/latex] and [latex]d=-3[/latex].
Try It
List the first five terms of the arithmetic sequence with [latex]{a}_{1}=1[/latex] and [latex]d=5[/latex] .
How To: Given any the first term and any other term in an arithmetic sequence, find a given term.
- Substitute the values given for [latex]{a}_{1},{a}_{n},n[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex] to solve for [latex]d[/latex].
- Find a given term by substituting the appropriate values for [latex]{a}_{1},n[/latex], and [latex]d[/latex] into the formula [latex]{a}_{n}={a}_{1}+\left(n - 1\right)d[/latex].
Example: Writing Terms of Arithmetic Sequences
Given [latex]{a}_{1}=8[/latex] and [latex]{a}_{4}=14[/latex] , find [latex]{a}_{5}[/latex] .
Try It
Given [latex]{a}_{3}=7[/latex] and [latex]{a}_{5}=17[/latex] , find [latex]{a}_{2}[/latex] .
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 5847, 5832. Authored by: Web-Work Rochester. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 23735. Authored by: Roy Shahbazian. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL