Learning outcomes
- Recognize when a situation calls for testing a hypothesis about a population proportion.
- Conduct a hypothesis test for a population proportion. State a conclusion in context.
- Interpret the P-value as a conditional probability in the context of a hypothesis test about a population proportion.
- Distinguish statistical significance from practical importance.
- From a description of a study, evaluate whether the conclusion of a hypothesis test is reasonable.
Introduction
In a hypothesis test, we test claims about a population parameter or the difference between two population parameters.
In this section, we look at the hypothesis test for a single population proportion. When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test. We also have to distinguish between testing a claim about a population proportion and estimating a population proportion.
Try It
Once we know that we are dealing with a single population proportion, we can conduct the hypothesis test. Recall that the first step of a hypothesis test is to determine the hypotheses. In the previous section, our hypotheses were in words. In this section, we use symbols. Recall that the symbol for the population proportion is p.
Example
Health Insurance Coverage

According to the Government Accountability Office, 80% of all college students ages 18 to 23 had health insurance coverage in 2006. The Patient Protection and Affordable Care Act passed in 2010 allowed young people under age 26 to stay on their parents’ health insurance policy. Has the proportion of college students ages 18 to 23 who have health insurance increased since 2006? A survey of 800 randomly selected college students ages 18 to 23 indicated that 83% of them had health insurance coverage.
- H0: p = 0.80 (No change; the proportion of college students ages 18 to 23 who have health insurance is still 80%.)
- Ha: p > 0.80 (The proportion of college students ages 18 to 23 who have health insurance is now greater than 80%.)
The results of the survey do not affect our hypotheses. We use the results to determine whether to reject the null hypothesis in favor of the alternative hypothesis.
Example
Internet Access

According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this percentage has changed since then. They survey 500 randomly selected children ages 8 to 18 and find that 430 of them have Internet access at home. The research question helps us form our hypotheses:
- H0: p = 0.84 (No change; the proportion of children with Internet access at home is the same.)
- Ha: p ≠ 0.84 (The proportion of children with Internet access at home has changed since 2009.)
Again, the results of the survey do not affect our hypotheses.
Example
Jury Selection

Jefferson Parish is a suburb of New Orleans, Louisiana. Its population is about 23% African American. Is there evidence that African Americans are underrepresented on juries in murder trials in Jefferson Parish? According to a New York Times article (June 4, 2007), there were 18 murder trials in Jefferson Parish between 1986 and 2007 in which the ethnicity of the jurors was known. Ten of the juries had no black jurors, 7 juries had 1 black juror, and 1 jury had 2 black jurors. The research question helps us to form our hypotheses:
- H0: p = 0.23 (No difference; the proportion of African Americans on juries in murder trials is the same as the proportion of African Americans in the population.)
- Ha: p < 0.23 (The proportion of African Americans on juries in murder trials is less than the proportion of African Americans in the population.)
Summary of Hypotheses
As a reminder, the null hypothesis is always a statement of equality. The alternative hypothesis is always a statement of inequality, using <, >, or ≠. So hypotheses take the form:
- H0: p = p0
- Ha: p < p0 or p > p0 or p ≠ p0
We use p0 to represent the proportion from the null hypothesis.
Now let’s look at how to determine P-values.
As we learned earlier, the P-value for a hypothesis test for a population proportion comes from a normal model for the sampling distribution of sample proportions. The normal distribution is an appropriate model for this sampling distribution if the expected number of success and failures are both at least 10. Using the symbols for the population proportion and sample size, a normal curve is a reasonable model if the following conditions are met: np ≥ 10 and n(1 − p) ≥ 10.
Summary of Requirements:
- The sample is a simple random sample.
- The conditions for a binomial experiment are satisfied.
- The expected number of successes and failures are at least 10 (np and n(1-p) are both > 10). Notes: these are calculated using the hypothesized proportion, p; 1 – p is often represented by q; and many references use a criteria of > 5 instead of 10.
Example
Health Insurance Coverage
Recall this example from the previous page. According to the Government Accountability Office, 80% of all college students (ages 18 to 23) had health insurance in 2006. The Patient Protection and Affordable Care Act of 2010 allowed young people under age 26 to stay on their parents’ health insurance policy. Has the proportion of college students (ages 18 to 23) who have health insurance increased since 2006? A survey of 800 randomly selected college students (ages 18 to 23) indicated that 83% of them had health insurance. Use a 0.05 level of significance.
Step 1: Determine the hypotheses.
We did this previously. The hypotheses are:
- H0: p = 0.80
- Ha: p > 0.80
where p is the proportion of college students ages 18 to 23 who have health insurance now.
Step 2: Collect the data.
In this random sample of 800 college students, 83% have health insurance. If 80% of all college students have health insurance, is this 3% difference statistically significant or due to chance? We need to find a P-value to answer this question. We must determine if we can use this data in a hypothesis test.
First note that the data are from a random sample. That is essential. Now we need to determine if a normal model is a good fit for the sampling distribution. Since we assume that the null hypothesis is true, we build the sampling distribution with the assumption that 0.80 is the population proportion. We check the following conditions, using 0.80 for p:
[latex]np=(800)(0.80)=640\text{ }\mathrm{and}\text{ }n(1-p)=(800)(1-0.80)=160[/latex]
Because these are both more than 10, we can use the normal model to find the P-value.
Step 3: Assess the evidence.
Now that we know that the normal distribution is an appropriate model for the sampling distribution, our next goal is to determine the P-value. The first step is to determine the z-score for the observed sample proportion (the data).
The sample proportion is 0.83. The formula for the z-score of a sample proportion is as follows:
[latex]Z=\frac{\stackrel{ˆ}{p}-p}{\sqrt{\frac{p(1-p)}{n}}}[/latex]
For this example, we calculate:
[latex]Z=\frac{0.83-0.80}{\sqrt{\frac{0.80(1-0.80)}{800}}}\approx 2.12[/latex]
This z-score is called the test statistic. It tells us the sample proportion of 0.83 is about 2.12 standard errors above the population proportion given in the null hypothesis. We use this statistic to find the P-value. The P-value describes the strength of the evidence against the null hypothesis.
The P-value is a probability that describes the likelihood of the data if the null hypothesis is true. More specifically, the P-value is the probability that sample results are as extreme as or more extreme than the data if the null hypothesis is true. The phrase “as extreme as or more extreme than” means farther from the center of the sampling distribution in the direction of the alternative hypothesis.
In this situation, we want the area to the right of 0.83 because the alternative hypothesis is a “greater-than” statement. The P-value, in this case, is the probability of getting a sample proportion equal to or greater than 0.83. Since we are using the standard normal curve to find probabilities, the P-value is the area to the right of the Z = 2.12.

We can find this area with a simulation or other technology.
The P-value is approximately 0.0170. (In Excel, use =1-NORM.S.DIST(2.12,1) =0.0170). Thus, the probability that a random sample proportion is at least as large as 0.83 is about 0.017 (if the population proportion is actually 0.80). If the null hypothesis is true, we observe sample proportions this high or higher only about 1.7% of the time.
The P-value is our evidence of statistical significance. It is a measure of whether random chance can explain the deviation of the data from the null hypothesis.
Step 4: State a conclusion.
To determine our conclusion, we compare the P-value to the level of significance, α = 0.05. If our data are predicted to occur by chance less than 5% of the time, we have reason to reject the null hypothesis and accept the alternative. Since our P-value of 0.017 is less than 0.05, we reject the null hypothesis. We state our conclusion in terms of the alternative hypothesis. We also state it in context.
The data from this study provides strong evidence that the proportion of all college students who have health insurance is now greater than 0.80 (P-value = 0.017). The 0.03 increase in the proportion who have health insurance since 2008 is statistically significant at the 0.05 level.
Alternatively, we can give the conclusion using the percentage rather than the decimal:
The data from this study provides strong evidence that the percentage of all college students who have health insurance is now greater than 80% (P-value = 0.017). The 3% increase in the percentage who have health insurance since 2008 is statistically significant at the 5% level.
Important Note
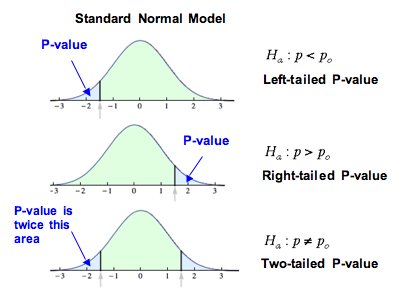
A hypothesis test can be one-tailed or two-tailed. The previous example was a one-tailed hypothesis test. The P-value was the area of the right tail. If the inequality in the alternative hypothesis is < or >, the test is one-tailed. If the inequality is ≠, the test is two-tailed.
Example
Internet Access
Recall the following example from the previous page. According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this percentage has changed since then. They survey 500 randomly selected children (ages 8 to 18) and find that 430 of them have Internet access at home.
Use a level of significance of α = 0.05 for this hypothesis test.
Step 1: Determine the hypotheses.
- H0: p = 0.84
- Ha: p ≠ 0.84
where p is the proportion of children ages 8 to 18 with Internet access at home now.
Step 2: Collect the data.
Our sample is random, so there is no problem there. Again, we want to determine whether the normal model is a good fit for the sampling distribution of sample proportions. Based on the null hypothesis, we will use 0.84 as our population proportion to check the conditions.
[latex]np=(500)(0.84)=420\text{ }\mathrm{and}\text{ }n(1-p)=(500)(1-0.84)=80[/latex]
Because these are both more than 10, we can use the normal model to find the P-value.
Step 3: Assess the evidence.
Since we can use the normal model, we need to calculate the z-test statistic for the sample proportion. We first calculate the sample proportion.
[latex]\stackrel{ˆ}{p}=\frac{x}{n}=\frac{430}{500}=0.86[/latex]
Next, we calculate our Z-score, the test statistic:
[latex]Z=\frac{\stackrel{ˆ}{p}-p}{\sqrt{\frac{p(1-p)}{n}}}=\frac{0.86-0.84}{\sqrt{\frac{0.84(1-0.84)}{500}}}\approx 1.22[/latex]
The sample proportion of 0.86 is about 1.22 standard errors above the population proportion given in the null hypothesis. Now we calculate the P-value. This is where the two-tailed nature of the test is important. The P-value is the probability of seeing a sample proportion at least as extreme as the one observed from the data if the null hypothesis is true.
In the previous example, only sample proportions higher than the null proportion were evidence in favor of the alternative hypothesis. In this example, any sample proportion that differs from 0.84 is evidence in favor of the alternative. Statistically significant differences are at least as extreme as the difference we see in the data. We want to determine the probability that the difference in either direction (above or below 0.84) is at least as large as the difference seen in the data, so we include sample proportions at or above 0.86 and sample proportions at or below 0.82. For this reason, we look at the area in both tails. Our simulation shows one tail, so we have to double this area.

The area above the test statistic of 1.22 is about 0.11. On this two-tailed test, we double this area to include the area in the left tail, below Z = −1.22. This gives us a P-value of approximately 0.22. (In Excel, use =2*(1-NORM.S.DIST(1.22,1)) = 0.22).
Our sample proportion was 0.02 above the population proportion from the null hypothesis. In a sample of size 500, we would observe a sample proportion 0.02 or more away from 0.84 about 22% of the time by chance alone.
Step 4: State a conclusion.
Again we compare the P-value to the level of significance, α = 0.05. In this case, the P-value of 0.22 is greater than 0.05, which means we do not have enough evidence to reject the null hypothesis. A sample result that could occur 22% of the time by chance alone is not statistically significant. Now we can state the conclusion in terms of the alternative hypothesis.
The data from this study does not provide evidence that is strong enough to conclude that the proportion of all children ages 8 to 18 who have Internet access at home has changed since 2009 (P-value = 0.22). The 2% change observed in the data is not statistically significant. These results can be explained by predictable variation in random samples.
Note about the Conclusion
In the conclusion above, we did not have enough evidence to reject the null hypothesis. As we noted in “Hypothesis Testing,” failing to reject the null hypothesis does not mean the null hypothesis is true.
In the case of the previous example, it is possible that the proportion of children who have Internet access at home has changed. But the data we gathered did not provide the evidence to detect that the proportion had changed significantly.
Researchers often note improvements that could be made in their research and suggest follow-up research that might be done. In our example, a second sample with a larger sample size might provide the evidence needed to reject the null hypothesis.
The important thing to keep in mind is that at the end of a hypothesis test, we never say that the null hypothesis is true.
Try It
California College Students Who Drink
According to the Centers for Disease Control and Prevention, 60% of all American adults ages 18 to 24 currently drink alcohol. Is the proportion of California college students who currently drink alcohol different from the proportion nationwide? A survey of 450 California college students indicates that 66% currently drink alcohol. The hypotheses were:
- H0: p = 0.60
- Ha: p ≠ 0.60
Click here to open the simulation
Try It
Coin Flips
Recall the scenario from the previous page. A psychic claims to be able to predict the outcome of coin flips before they happen. Someone who guesses randomly will predict about half of coin flips correctly. In 100 flips, the psychic correctly predicts 57 flips. Do the results of this test indicate that the psychic does better than random guessing? The hypotheses are
- H0: p = 0.50
- Ha: p > 0.50
where p is the proportion of correct coin flip predictions by the psychic.
Click here to open the simulation
Try It
More about the P-Value
The P-value is a probability that describes the likelihood of the data if the null hypothesis is true. More specifically, the P-value is the probability that sample results are as extreme as or more extreme than the data if the null hypothesis is true. The phrase “as extreme as or more extreme than” means farther from the center of the sampling distribution in the direction of the alternative hypothesis.
More generally, we view the P-value a description of the strength of the evidence against the null hypothesis and in support of the alternative hypothesis. But the P-value is a probability about sample results, not about the null or alternative hypothesis.
One More Note about P-Values and the Significance Level
You may wonder why 5% is often selected as the significance level in hypothesis testing and why 1% is also a commonly used level. It is largely due to just convenience and tradition. When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly, these are arbitrary levels.
The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics. But it’s important to remember that there is really a continuous range of increasing confidence toward the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between the P-values 0.049 and 0.051, and it would be foolish to declare one case definitely a “real” effect and the other case definitely a “random” effect. In either case, the study results are roughly 5% likely by chance if there’s no actual effect.
Whether such a P-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision and the extent to which the hypothesized effect might contradict our prior experience or previous studies.
Example
Sample Size and Hypothesis Testing
Consider our earlier example about teenagers and Internet access. According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this number has changed since then. The hypotheses we tested were:
- H0: p = 0.84
- Ha: p ≠ 0.84
The original sample consisted of 500 children, and 86% of them had Internet access at home. The P-value was about 0.22, which was not strong enough to reject the null hypothesis. There was not enough evidence to show that the proportion of all U.S. children ages 8 to 18 have Internet access at home.
Suppose we sampled 2,000 children and the sample proportion was still 86%. Our test statistic would be Z ≈ 2.44, and our P-value would be about 0.015. The larger sample size would allow us to reject the null hypothesis even though the sample proportion was the same.

Why does this happen? Larger samples vary less, so a sample proportion of 0.86 is more unusual with larger samples than with smaller samples if the population proportion is really 0.84. This means that if the alternative hypothesis is true, a larger sample size will make it more likely that we reject the null. Therefore, we generally prefer a larger sample as we have seen previously.
Drawing Conclusions from Hypothesis Tests
It is tempting to get involved in the details of a hypothesis test without thinking about how the data was collected. Whether we are calculating a confidence interval or performing a hypothesis test, the results are meaningless without a properly designed study. Consider the following exercises about how data collection can affect the results of a study.
Try It
Let’s Summarize
In this section, we looked at the four steps of a hypothesis test as they relate to a claim about a population proportion.
Step 1: Determine the hypotheses.
- The hypotheses are claims about the population proportion, p.
- The null hypothesis is a hypothesis that the proportion equals a specific value, p0.
- The alternative hypothesis is the competing claim that the parameter is less than, greater than, or not equal to p0.
Step 2: Collect the data.
Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n(1 − p) ≥ 10.
Step 3: Assess the evidence.
- Determine the test statistic which is the z-score for the sample proportion. The formula is: [latex]Z=\frac{\stackrel{ˆ}{p}-{p}_{0}}{\sqrt{\frac{{p}_{0}(1-{p}_{0})}{n}}}[/latex]
- Use the test statistic, together with the alternative hypothesis to determine the P-value. You can use a standard normal table (or Z-table) or technology (such as the simulations on the second page of this topic) to find the P-value.
- If the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.
Step 4: Give the conclusion.
- A small P-value says the data is unlikely to occur if the null is true. If the P-value is less than or equal to the significance level, we reject the null hypothesis and accept the alternative hypothesis instead.
- If the P-value is greater than the significance level, we say we “fail to reject” the null hypothesis. We never say that we “accept” the null hypothesis. We just say that we don’t have enough evidence to reject it. This is equivalent to saying we don’t have enough evidence to support the alternative hypothesis.
- We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept Ha or fail to accept Ha) and should include the P-value.
Other Hypothesis Testing Notes
Remember that the P-value is the probability of seeing a sample proportion as extreme as the one observed from the data if the null hypothesis is true. The probability is about the random sample, not about the null or alternative hypothesis.
A larger sample size makes it more likely that we will reject the null hypothesis if the alternative is true. Another way of thinking about this is that increasing the sample size will decrease the likelihood of a type II error. Recall that a type II error is failing to reject the null hypothesis when the alternative is true.
Increasing the sample size can have the unintended effect of making the test sensitive to differences so small they don’t matter. A statistically significant difference is one large enough that it is unlikely to be due to sampling variability alone. Even a difference so small that it is not important can be statistically significant if the sample size is big enough.
Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless. No statistical methods can create useful information if our data comes from convenience or voluntary response samples. Additionally, the results of a hypothesis test apply only to the population from whom the sample was chosen.