$x$-intercepts of a Function and Solutions of an Equation

How can we find the $x$-intercepts (or real zeros) of a function $y=f(x)$? First, we need to set $y=0$ because all $x$-intercepts are on the $x$-axis and any points on the $x$-axis have zero for its $y$-coordinate. Then, we need to solve the equation $f(x)=0$. For example, to find the $x$-intercepts (or real zeros) of a function $f(x)=\frac{1}{7}x(x+3)(x-5)$, we need to solve the equation $\frac{1}{7}x(x+3)(x-5)=0$. From this equation, we can find $x=-3, 0, 5$ as its solutions and can write them as $(-3, 0)$, $(0, 0)$, and $(5, 0)$ because those solutions are the $x$ values when its $y$ value is zero. So, we can conclude that the solutions of the equation $\frac{1}{7}x(x+3)(x-5)=0$ is actually the $x$-intercepts (or real zeros) of the function $f(x)=\frac{1}{7}x(x+3)(x-5)$. We can confirm this relation from the graph of the function $f(x)=\frac{1}{7}x(x+3)(x-5)$ as well.

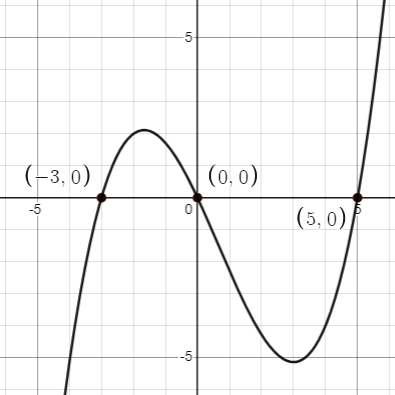
Figure 2. Graph of $f(x)=\frac{1}{7}x(x+3)(x-5)$

In Figure 2, we can find the solutions of the equation $\frac{1}{7}x(x+3)(x-5)=0$ by locating the $x$-intercepts of the graph of the function $f(x)=\frac{1}{7}x(x+3)(x-5)$.

Distinct Parts of a Graph of a Function

Now let’s consider more points on the graph. As we can see in Figure 2, some parts of the graph are above the $x$-axis, some parts of the graph are on the $x$-axis, and some parts of the graph are below the $x$-axis. Try the following DESMOS activity to explore the relationship between those distinct parts of the function and the sign of its $y$ values:

From the DESMOS activity above, we can conclude the followings: