Learning OUTCOMES
- Recognize symmetry of a function.
- Determine even and odd functions.
- Determine symmetry of an equation (with two variables) graphically.
- Determine symmetry of an equation (with two variables) algebraically.
Symmetry of a Function
The graphs of certain functions have symmetrical properties that help us understand the function and the shape of its graph. For example, consider the function [latex]f(x)=x^4-2x^2-3[/latex] shown in Figure 2(a). If we take the part of the curve that lies to the right of the [latex]y[/latex]-axis and flip it over the [latex]y[/latex]-axis, it lays exactly on top of the curve to the left of the [latex]y[/latex]-axis. In this case, we say the function has symmetry about the [latex]y[/latex]-axis. On the other hand, consider the function [latex]f(x)=x^3-4x[/latex] shown in Figure 2(b). If we take the graph and rotate it 180° about the origin, the new graph will look exactly same. In this case, we say the function is symmetric about the origin.
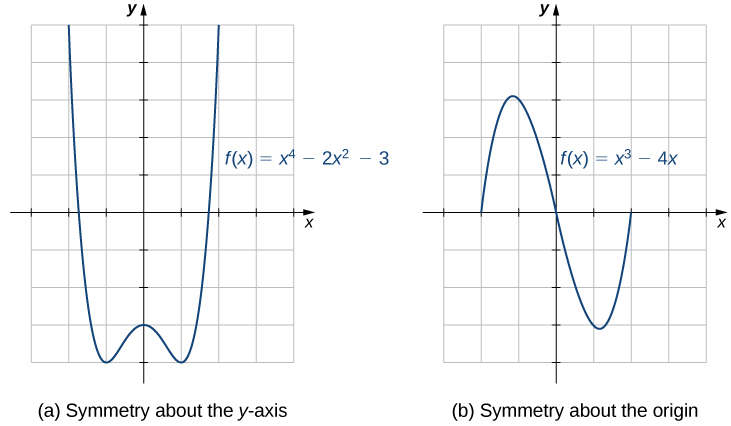
In other words, if we reflect the graph (a) about the [latex]y[/latex]-axis, we can see that the new graph looks exactly same as the original graph. Also, if we reflect the graph (b) about the origin (or about the [latex]x[/latex]-axis and the [latex]y[/latex]-axis), the new graph looks exactly same as the original graph. To make it happen, [latex](-x, y)[/latex] should be on the graph (a) whenever [latex](x, y)[/latex] is on the graph (a) and [latex](-x, -y)[/latex] should be on the graph (b) whenever [latex](x, y)[/latex] is on the graph (b). What does this mean?
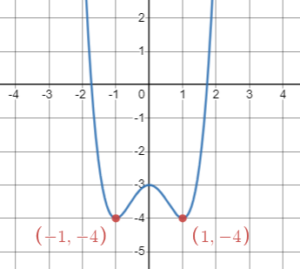
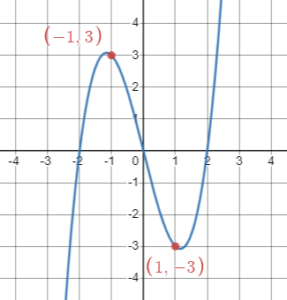
For example, if [latex](1, -4)[/latex] is on the graph (a), [latex](-1, -4)[/latex] should be on the graph (a) because it is symmetric about the [latex]y[/latex]-axis. Also, if [latex](1, -3)[/latex] is on the graph (b), [latex](-1, 3)[/latex] should be on the graph (b) because it is symmetric about the origin.
 |
 |
A GENERAL NOTE: SYmmetry of a Function
- A function is symmetric about the y-axis if [latex](-x, y)[/latex] is on the graph of the function whenever [latex](x, y)[/latex] is on the graph.
- A function is symmetric about the origin if [latex](-x, -y)[/latex] is on the graph of the function whenever [latex](x, y)[/latex] is on the graph.
Even and Odd Functions
If we are given the graph of a function, it is easy to see whether the graph has one of these symmetry properties. But without a graph, how can we determine algebraically whether a function [latex]f[/latex] has symmetry? Looking at Figure 2(a) again, we see that since [latex]f[/latex] is symmetric about the [latex]y[/latex]-axis, if the point [latex](x, y)[/latex] is on the graph, the point [latex](-x, y)[/latex] is on the graph. In other words, [latex]f(-x)=f(x)[/latex]. If a function [latex]f[/latex] has this property, we say [latex]f[/latex] is an even function, which has symmetry about the [latex]y[/latex]-axis. For example, [latex]f(x)=x^2[/latex] is even because
[latex]f(-x)=(-x)^2=x^2=f(x)[/latex].
In contrast, looking at Figure 2(b) again, if a function [latex]f[/latex] is symmetric about the origin, then whenever the point [latex](x, y)[/latex] is on the graph, the point [latex](-x, -y)[/latex] is also on the graph. In other words, [latex]f(-x)=-f(x)[/latex]. If [latex]f[/latex] has this property, we say [latex]f[/latex] is an odd function, which has symmetry about the origin. For example, [latex]f(x)=x^3[/latex] is odd because
[latex]f(-x)=(-x)^3=-x^3=-f(x)[/latex].
A GENERAL NOTE: Even and Odd Functions
- If [latex]f(-x)=f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex], then [latex]f[/latex] is an even function. An even function is symmetric about the [latex]y[/latex]-axis.
- If [latex]f(-x)=-f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex], then [latex]f[/latex] is an odd function. An odd function is symmetric about the origin.
EXAMPLE: EVEN AND ODD FUNCTIONS
Determine whether each of the following functions is even, odd, or neither.
-
- [latex]f(x)=-5x^4+7x^2-2[/latex]
- [latex]g(x)=2x^5-4x+5[/latex]
- [latex]h(x)=\frac{3x}{x^2+1}[/latex]
Try It
Determine whether [latex]f(x)=4x^3-5x[/latex] is even, odd, or neither.
Determine Symmetry of an Equation (with two variables) Graphically
How to: Determine Symmetry of an Equation (with two variables) Graphically
- An equation with two variables is symmetric about the x-axis if we reflect its graph about the [latex]x[/latex]-axis and the new graph looks exactly same as its original graph.
- An equation with two variables is symmetric about the y-axis if we reflect the graph about the [latex]y[/latex]-axis and the new graph looks exactly same as its original graph.
- An equation is symmetric about the origin if we rotate the graph 180° about the origin (or reflect the graph about the [latex]x[/latex]-axis and [latex]y[/latex]-axis) and the new graph looks exactly same as its original graph.
Example: Determine Symmetry of an Equation (with two variables) Graphically
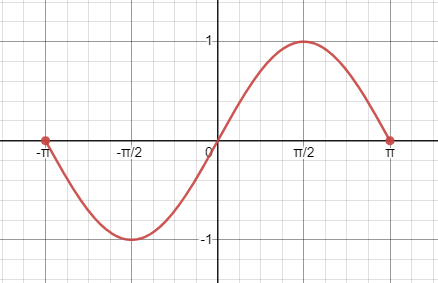
Using the given graph of an equation, determine whether the graph is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.
|
1.
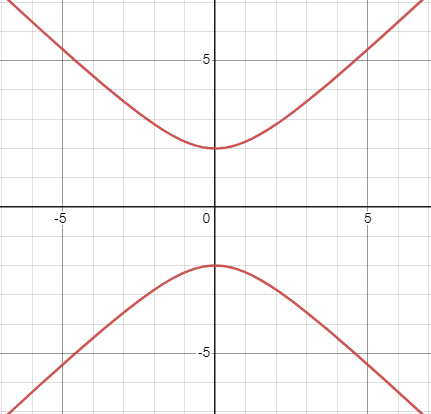 |
2.
 |
|
3.
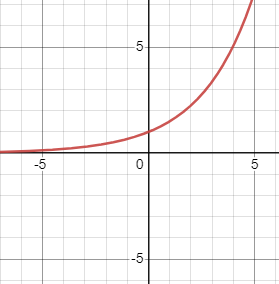 |
4.
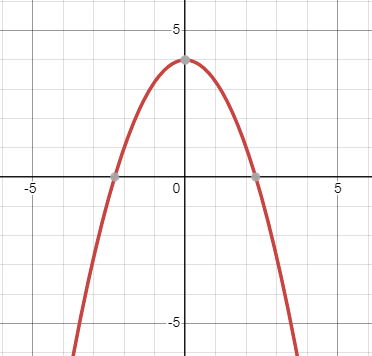 |
|
5.
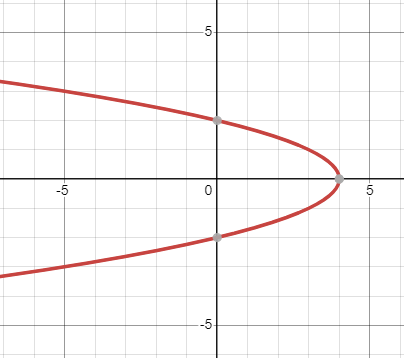 |
6.
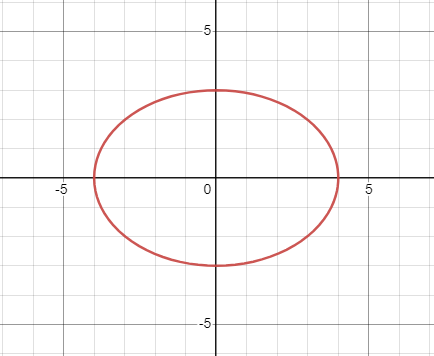 |
Determine Symmetry of an Equation (with two variables) Algebraically
How to: Determine Symmetry of an Equation (with two variables) Algebraically
- Substitute [latex]-y[/latex] for all the [latex]y[/latex]‘s in the equation.
- Simplify the equation.
- If the simplified equation is exactly same as the original equation, the equation is symmetric about the [latex]x[/latex]-axis.
- Substitute [latex]-x[/latex] for all the [latex]x[/latex]‘s in the equation.
- Simplify the equation.
- If the simplified equation is exactly same as the original equation, the equation is symmetric about the [latex]y[/latex]-axis.
- Substitute [latex]-x[/latex] for all the [latex]x[/latex]‘s and [latex]-y[/latex] for all the [latex]y[/latex]‘s in the equation.
- Simplify the equation.
- If the simplified equation is exactly same as the original equation, the equation is symmetric about the origin.
Example: Determine Symmetry of a Function Algebraically
Determine whether each equation is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.
- [latex]x^2+y^2=9[/latex]
- [latex]y=x^2-5[/latex]
Try It
Determine whether each equation is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.
- [latex]y=x^3+1[/latex]
- [latex]y^2+4x-8=0[/latex]
- [latex]4x^2+9y^2=36[/latex]
- [latex]y=\sqrt[3]{x}[/latex]
- [latex]y=x^6-7x^2+3[/latex]
- [latex]y=\frac{x}{x^2-1}[/latex]
Candela Citations
- Symmetry of a Function. Authored by: Michelle Eunhee Chung. Provided by: Georgia State University. License: CC BY: Attribution
