Solving Equations with One Variable using One Function

As we have seen, we can solve an equation [latex]f(x)=0[/latex] by finding the [latex]x[/latex]-intercepts of its function [latex]y=f(x)[/latex], and the graph of [latex]y=f(x)[/latex] makes the process much easier. For example, we can easily locate the [latex]x[/latex]-intercept of [latex]f(x)=-\frac{3}{4}x+3[/latex] from its graph, and we can conclude that the solution of [latex]-\frac{3}{4}x+3=0[/latex] is [latex]x=4[/latex].

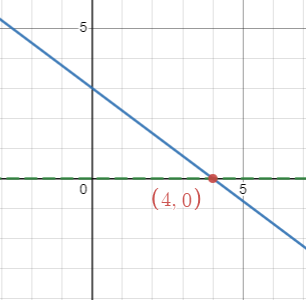
Figure 3. Graph of [latex]f(x)=-\frac{3}{4}x+3[/latex]

Moreover, this method helps us to solve more complex equations as well. For example, to solve [latex]x+\frac{3}{x}-4=0[/latex], we should consider the graph of [latex]f(x)=x+\frac{3}{x}-4[/latex] and find the [latex]x[/latex]-intercepts. As we can read on the graph, the [latex]x[/latex]-intercepts of this function are [latex](1, 0)[/latex] and [latex](3, 0)[/latex]. So, the solutions of the equation are [latex]x=1, 3[/latex].

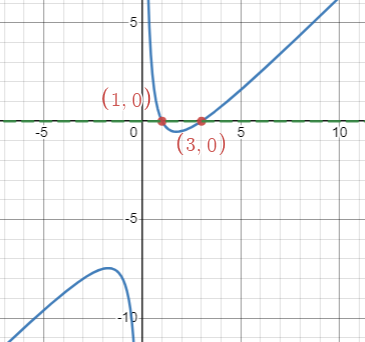
Figure 4. Graph of [latex]f(x)=x+\frac{3}{x}-4[/latex]

Example: Solving [latex]f(x)=0[/latex] Graphically

Solve the equation graphically. Use a graphing tool.

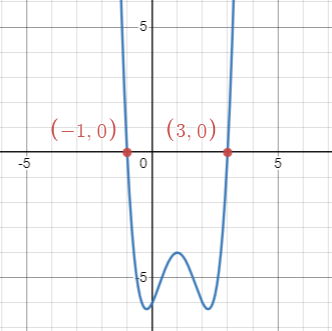
[latex]x^3-x-4x^2+4=0[/latex]

 

Show Graph

Show Answer

Let [latex]f(x)=x^3-x-4x^2+4[/latex]. Then [latex]x=-1, 1, 4[/latex]. 

Try It

Solve the equation graphically. Use a graphing tool.

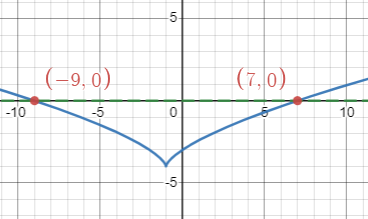
[latex](x-1)^4-3(x-1)^2-4=0[/latex]

 

Show Graph

Show Answer

Let [latex]f(x)=(x-1)^4-3(x-1)^2-4[/latex]. Then, [latex] x=-1, 3[/latex].

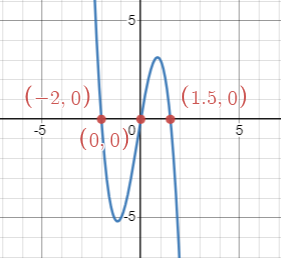
Example: Solving [latex]f(x)=0[/latex] Graphically

Solve the equation graphically. Use a graphing tool.

[latex]\sqrt[3]{(x+1)^2}-4=0[/latex]

 

Show Graph

Show Answer

Let [latex]f(x)=\sqrt[3]{(x+1)^2}-4[/latex]. Then, [latex]x=-9, 7[/latex]

Try It

Solve the equation graphically. Use a graphing tool.

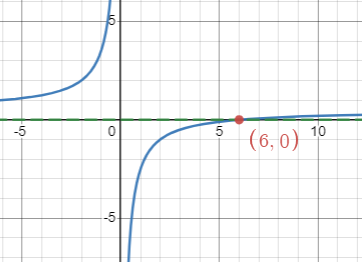
[latex]\frac{x-3}{x}-\frac{1}{2}=0[/latex]

 

Show Graph

Show Answer

Let [latex]f(x)=\frac{x-3}{x}-\frac{1}{2}[/latex]. Then, [latex]x=6[/latex]

Solving Equations with One Variable using Multiple Functions

Now we know how to solve equations graphically. But what if the given equation is not in “[latex]f(x)=0[/latex]” form? How can we apply the method we used in the previous examples? There are two different ways to solve this equation:

1. Move all terms to the left and make it in “[latex]f(x)=0[/latex]” form. Then, graph and find the [latex]x[/latex]-intercepts.
2. Let “[latex]f(x)=[/latex](lefthand side)” and “[latex]g(x)=[/latex](righthand side).” Then, graph and find the intersecting points of [latex]f(x)[/latex] and [latex]g(x)[/latex]. The [latex]x[/latex]-coordinates are the solutions of the equation.

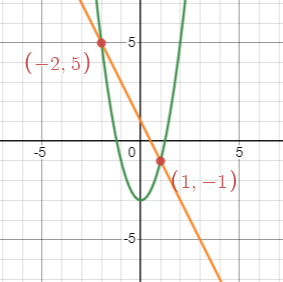
Example: Solving [latex]f(x)=g(x)[/latex] Graphically

Solve the equation graphically. Use a graphing tool.

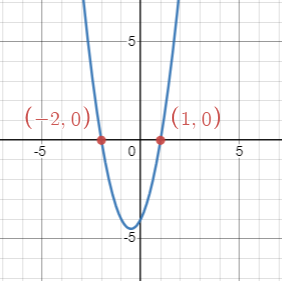
[latex]2x^2-3=-2x+1[/latex]

Show Answer

Method 1

Move all terms to the left: [latex]2x^2-3+2x-1=0[/latex]*

[latex]2x^2+2x-4=0[/latex]

Let [latex]f(x)=2x^2+2x-4[/latex].

* If you are using a graphing tool, you don’t need to simplify the equation. Just let [latex]f(x)=2x^2-3-(-2x+1)[/latex] or  [latex]f(x)=2x^2-3+2x-1[/latex].

Since the [latex]x[/latex]-intercepts are [latex](-2, 0), (1, 0)[/latex], the solutions of [latex]2x^2-3=-2x+1[/latex] are [latex]x=-2, 1[/latex].

Method 2

Let [latex]f(x)=2x^2-3[/latex] and [latex]g(x)=-2x+1[/latex].

Since the intersecting points are [latex](-2, 5), (1, -1)[/latex], the solutions of [latex]2x^2-3=-2x+1[/latex] are [latex]x=-2, 1[/latex].

Try It

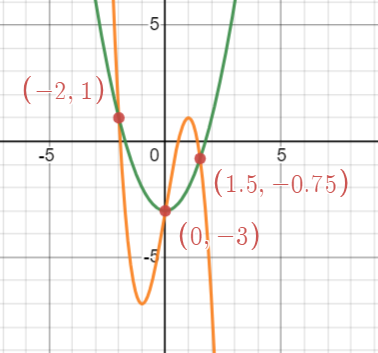
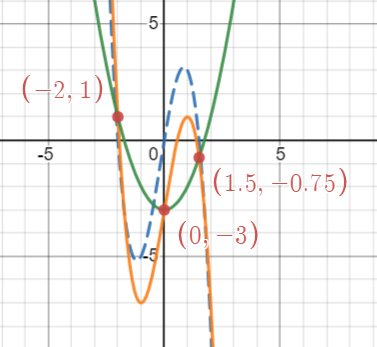
Solve the equation graphically. Use a graphing tool.

[latex]-2x^3+6x-3=x^2-3[/latex]

Show Answer

Move all terms to the lefthand side: [latex]-2x^3+6x-3-x^2+3=0[/latex]. Then let [latex]f(x)=-2x^3-x^2+6x[/latex]. Since the [latex]x[/latex]-intercepts are [latex](-2, 0), (\frac{3}{2}, 0)[/latex], the solutions are [latex]x=-2, \frac{3}{2}[/latex].

OR

Let [latex]g(x)=-2x^3+6x-3[/latex] and [latex]h(x)=x^2-3[/latex]. Since the intersecting points of [latex]g(x)[/latex] and [latex]h(x)[/latex] are [latex](-2, 1)[/latex] and [latex](\frac{3}{2}, -\frac{3}{4})[/latex], the solutions are [latex]x=-2, \frac{3}{2}[/latex].