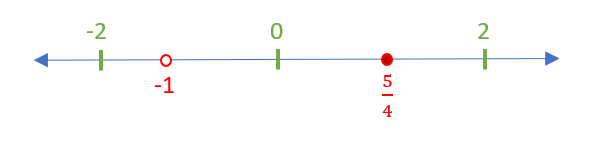Learning Outcomes
- Solve rational inequalities using boundary value method.
Solving Rational Inequalities using Boundary Value Method
Any inequality that can be put into one of the following forms
[latex]f(x)>0, f(x) \geq 0, f(x)<0, or f(x) \leq 0[/latex], where [latex]f[/latex] is a rational function
is called rational inequality.
How To: Solve Rational Inequalities
- Find restriction(s) of the given rational expression(s) in the inequality. The restriction(s) is(are) the boundary point(s).
- Rewrite the given rational inequality as an equation by replacing the inequality symbol with the equal sign.
- Solve the rational equation. The real solution(s) of the equation is(are) the boundary point(s).
- Plot the boundary point(s) from Step 1 & 3 on a number line.
[latex]\Rightarrow[/latex] Use an open circle ALL restrictions.
[latex]\Rightarrow[/latex] Use an open circle when the given inequality has [latex]<[/latex] or [latex]>[/latex]
[latex]\Rightarrow[/latex] Use a closed circle when the given inequality has [latex]\leq[/latex] or [latex]\geq[/latex]. - Choose one number, which is called a test value, from each interval and test the intervals by evaluating the given inequality at that number.
[latex]\Rightarrow[/latex] If the inequality is TRUE, then the interval is a solution of the inequality.
[latex]\Rightarrow[/latex] If the inequality is FALSE, then the interval is not a solution of the inequality. - Write the solution set (usually in interval notation), selecting the interval(s) from Step 5.
Example: Solving Rational Inequality using Boundary Value Method
Solve the rational inequality using boundary value method. Graph the solution set and write the solution in interval notation.
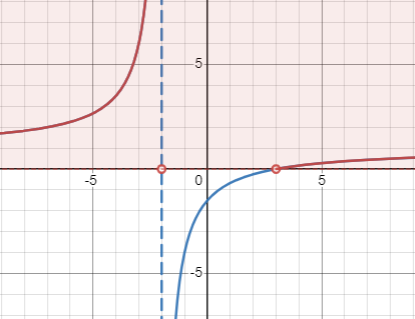
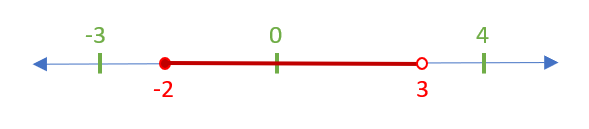
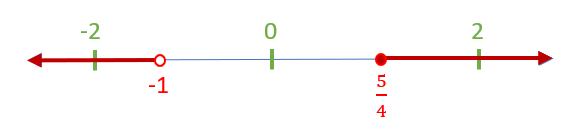
[latex]\frac{2x-1}{x+2} > 1[/latex]
Show Answer
Try It
Solve the rational inequality using boundary value method. Graph the solution set and write the solution in interval notation.
[latex]\frac{5x}{x-3} \leq 2[/latex]
Show Answer
Try It
Solve the rational inequality using boundary value method. Graph the solution set and write the solution in interval notation.
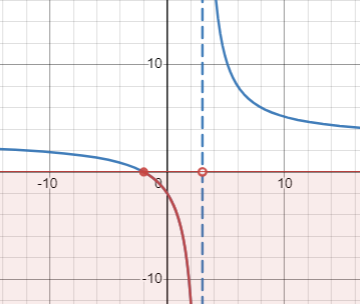
[latex]\frac{4x-5}{x+1} \geq 0[/latex]
Show Answer
Candela Citations
CC licensed content, Original
- Solving Rational Inequalities. Authored by: Michelle Eunhee Chung. Provided by: Georgia State University. License: CC BY: Attribution