▪ Symmetry of a Function

Learning OUTCOMES

  • Recognize symmetry of a function.
  • Determine even and odd functions.
  • Determine symmetry of an equation (with two variables) graphically.
  • Determine symmetry of an equation (with two variables) algebraically.

Symmetry of a Function

The graphs of certain functions have symmetrical properties that help us understand the function and the shape of its graph. For example, consider the function [latex]f(x)=x^4-2x^2-3[/latex] shown in Figure 2(a). If we take the part of the curve that lies to the right of the [latex]y[/latex]-axis and flip it over the [latex]y[/latex]-axis, it lays exactly on top of the curve to the left of the [latex]y[/latex]-axis. In this case, we say the function has symmetry about the [latex]y[/latex]-axis. On the other hand, consider the function [latex]f(x)=x^3-4x[/latex] shown in Figure 2(b). If we take the graph and rotate it 180° about the origin, the new graph will look exactly same. In this case, we say the function is symmetric about the origin.

Figure 2. (a) A graph that is symmetric about the y-axis.   (b) A graph that is symmetric about the origin.

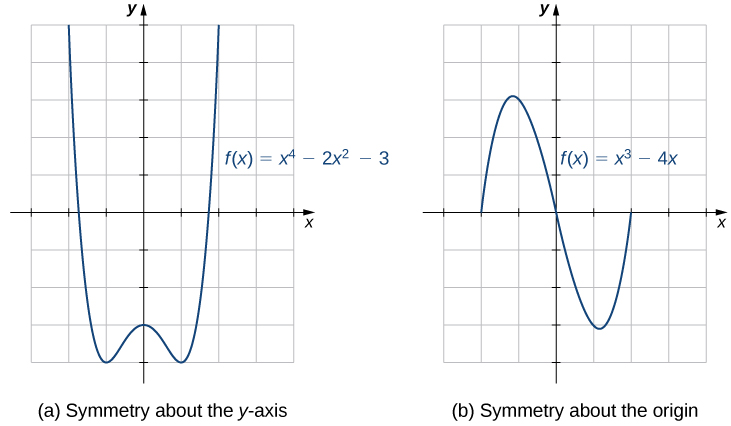
In other words, if we reflect the graph (a) about the [latex]y[/latex]-axis, we can see that the new graph looks exactly same as the original graph. Also, if we reflect the graph (b) about the origin (or about the [latex]x[/latex]-axis and the [latex]y[/latex]-axis), the new graph looks exactly same as the original graph. To make it happen, [latex](-x, y)[/latex] should be on the graph (a) whenever [latex](x, y)[/latex] is on the graph (a) and [latex](-x, -y)[/latex] should be on the graph (b) whenever [latex](x, y)[/latex] is on the graph (b). What does this mean?

For example, if [latex](1, -4)[/latex] is on the graph (a), [latex](-1, -4)[/latex] should be on the graph (a) because it is symmetric about the [latex]y[/latex]-axis. Also, if [latex](1, -3)[/latex] is on the graph (b), [latex](-1, 3)[/latex] should be on the graph (b) because it is symmetric about the origin.

A GENERAL NOTE: SYmmetry of a Function

  • A function is symmetric about the y-axis if [latex](-x, y)[/latex] is on the graph of the function whenever [latex](x, y)[/latex] is on the graph.
  • A function is symmetric about the origin if [latex](-x, -y)[/latex] is on the graph of the function whenever [latex](x, y)[/latex] is on the graph.

Even and Odd Functions

If we are given the graph of a function, it is easy to see whether the graph has one of these symmetry properties. But without a graph, how can we determine algebraically whether a function [latex]f[/latex] has symmetry? Looking at Figure 2(a) again, we see that since [latex]f[/latex] is symmetric about the [latex]y[/latex]-axis, if the point [latex](x, y)[/latex] is on the graph, the point [latex](-x, y)[/latex] is on the graph. In other words, [latex]f(-x)=f(x)[/latex]. If a function [latex]f[/latex] has this property, we say [latex]f[/latex] is an even function, which has symmetry about the [latex]y[/latex]-axis. For example, [latex]f(x)=x^2[/latex] is even because

[latex]f(-x)=(-x)^2=x^2=f(x)[/latex].

In contrast, looking at Figure 2(b) again, if a function [latex]f[/latex] is symmetric about the origin, then whenever the point [latex](x, y)[/latex] is on the graph, the point [latex](-x, -y)[/latex] is also on the graph. In other words, [latex]f(-x)=-f(x)[/latex]. If [latex]f[/latex] has this property, we say [latex]f[/latex] is an odd function, which has symmetry about the origin. For example, [latex]f(x)=x^3[/latex] is odd because

[latex]f(-x)=(-x)^3=-x^3=-f(x)[/latex].

A GENERAL NOTE: Even and Odd Functions

  • If [latex]f(-x)=f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex], then [latex]f[/latex] is an even function. An even function is symmetric about the [latex]y[/latex]-axis.
  • If [latex]f(-x)=-f(x)[/latex] for all [latex]x[/latex] in the domain of [latex]f[/latex], then [latex]f[/latex] is an odd function. An odd function is symmetric about the origin.

EXAMPLE: EVEN AND ODD FUNCTIONS

Determine whether each of the following functions is even, odd, or neither.

    1. [latex]f(x)=-5x^4+7x^2-2[/latex]
    2. [latex]g(x)=2x^5-4x+5[/latex]
    3. [latex]h(x)=\frac{3x}{x^2+1}[/latex]

Try It

Determine whether [latex]f(x)=4x^3-5x[/latex] is even, odd, or neither.

Determine Symmetry of an Equation (with two variables) Graphically

How to: Determine Symmetry of an Equation (with two variables) Graphically

  • An equation with two variables is symmetric about the x-axis if we reflect its graph about the [latex]x[/latex]-axis and the new graph looks exactly same as its original graph.
  • An equation with two variables is symmetric about the y-axis if we reflect the graph about the [latex]y[/latex]-axis and the new graph looks exactly same as its original graph.
  • An equation is symmetric about the origin if we rotate the graph 180° about the origin (or reflect the graph about the [latex]x[/latex]-axis and [latex]y[/latex]-axis) and the new graph looks exactly same as its original graph.

Example: Determine Symmetry of an Equation (with two variables) Graphically

Using the given graph of an equation, determine whether the graph is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.

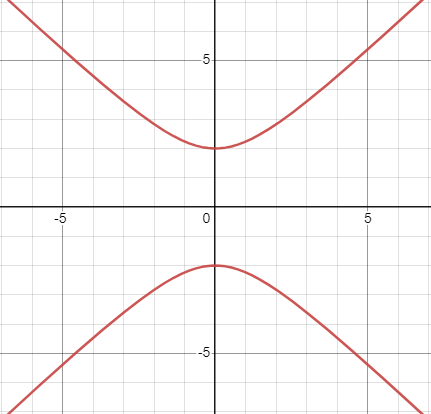1. A graph of hyperbola
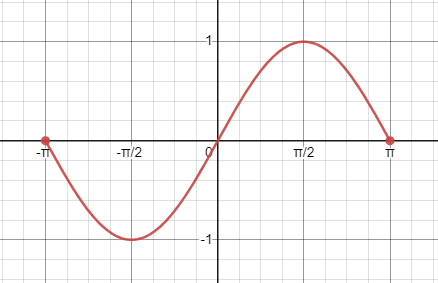2. A graph of sine function
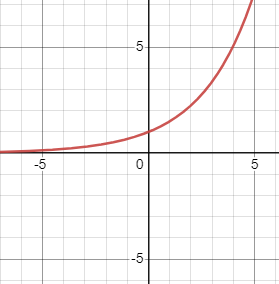3. A graph of exponential function
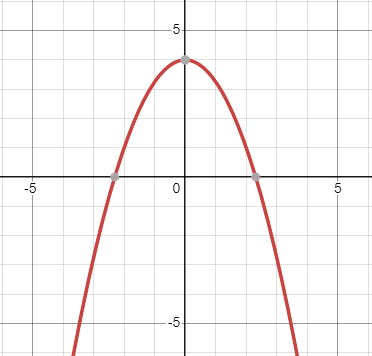4. A graph of quadratic function
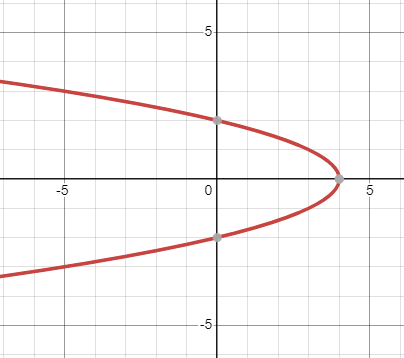5. A graph of x+y^2=4
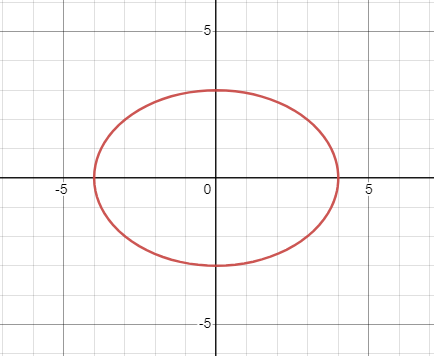6. A graph of ellipse

Determine Symmetry of an Equation (with two variables) Algebraically

How to: Determine Symmetry of an Equation (with two variables) Algebraically

Symmetry about the x-axis
  1. Substitute [latex]-y[/latex] for all the [latex]y[/latex]‘s in the equation.
  2. Simplify the equation.
  3. If the simplified equation is exactly same as the original equation, the equation is symmetric about the [latex]x[/latex]-axis.

 

Symmetry about the y-axis
  1. Substitute [latex]-x[/latex] for all the [latex]x[/latex]‘s in the equation.
  2. Simplify the equation.
  3. If the simplified equation is exactly same as the original equation, the equation is symmetric about the [latex]y[/latex]-axis.

 

Symmetry about the origin
  1. Substitute [latex]-x[/latex] for all the [latex]x[/latex]‘s and [latex]-y[/latex] for all the [latex]y[/latex]‘s in the equation.
  2. Simplify the equation.
  3. If the simplified equation is exactly same as the original equation, the equation is symmetric about the origin.

Example: Determine Symmetry of a Function Algebraically

Determine whether each equation is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.

  1. [latex]x^2+y^2=9[/latex]
  2. [latex]y=x^2-5[/latex]

Try It

Determine whether each equation is symmetric about [latex]x[/latex]-axis, [latex]y[/latex]-axis, and/or the origin.

  1. [latex]y=x^3+1[/latex]
  2. [latex]y^2+4x-8=0[/latex]
  3. [latex]4x^2+9y^2=36[/latex]
  4. [latex]y=\sqrt[3]{x}[/latex]
  5. [latex]y=x^6-7x^2+3[/latex]
  6. [latex]y=\frac{x}{x^2-1}[/latex]