▪ Symmetry of a Point

Learning OUTCOMES

  • Find points that are symmetric to a point about the x-axis, the y-axis, and the origin.

Symmetry of a Point

Let’s consider a point [latex](2, 5)[/latex] on a coordinate plane. What will happen if reflect the point across the [latex]x[/latex]-axis, the [latex]y[/latex]-axis, and the origin?

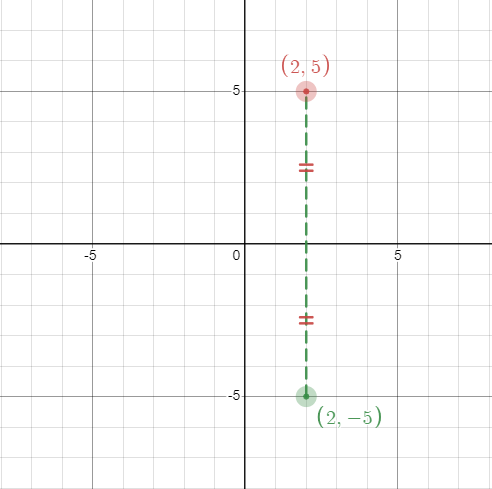(a) When (2, 5) is reflected across the x-axis, it becomes (2, -5). Those two points have the same distance from the x-axis.
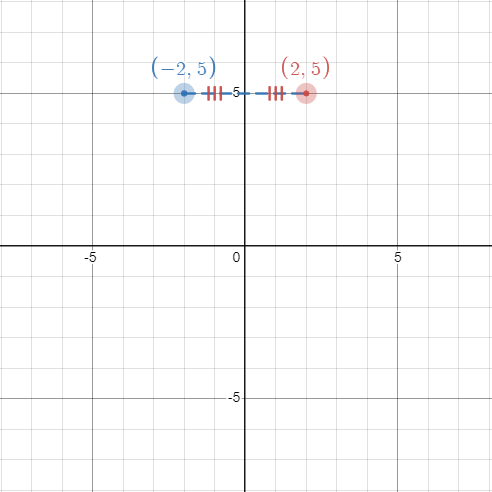(b) When (2, 5) is reflected across the y-axis, it becomes (-2, 5). Those two points have the same distance from the y-axis.
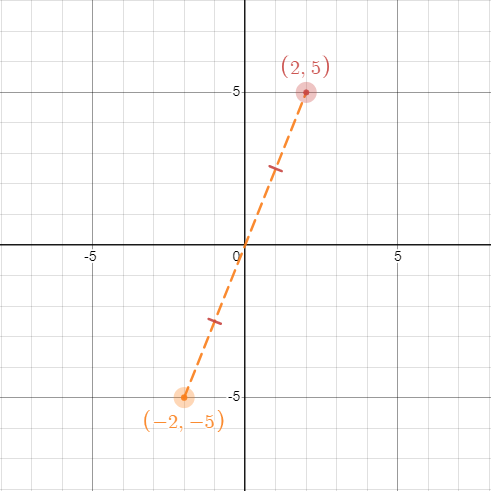(a, b) becomes (-a, -b) when a point reflected across the origin(c) When (2, 5) is reflected across the origin, which is reflected across the x-axis and the y-axis, it becomes (-2, -5). Those two points have the same distance from the origin.
Figure 1. (a) The point that is symmetric to [latex](2, 5)[/latex] about the [latex]x[/latex]-axis.   (b) The point that is symmetric to [latex](2, 5)[/latex] about the [latex]y[/latex]-axis.   (c) The point that is symmetric to [latex](2, 5)[/latex] about the origin.

Use the following DESMOS exercise to investigate more: [DESMOS] Symmetry of a Point or [DESMOS Classroom] Symmetry of a Point

General Note: Symmetry of a Point

(a) When we reflect a point across the x-axis, its y-coordinate will become its opposite number while its x-coordinate stays as is. So, the point that is symmetric to (a, b) about the x-axis is (a, -b).

(b) When we reflect a point across the y-axis, its x-coordinate will become its opposite number while its y-coordinate stays as is. So, the point that is symmetric to (a, b) about the y-axis is (-a, b).

(c) When we reflect a point across the origin, both x- and y-coordinates will become its opposite number, respectively. So, the point that is symmetric to (a, b) about the origin is (-a, -b).

EXAMPLE: Symmetry of a Point

Find the points that are symmetric to it about (a) the [latex]x[/latex]-axis, (b) the [latex]y[/latex]-axis, and (c) the origin.

  1. [latex](-7, 9)[/latex]
  2. [latex](3, -1)[/latex]
  3. [latex](-11, -8)[/latex]
  4. [latex](6, 0)[/latex]
  5. [latex](0, -5)[/latex]
  6. [latex](0, 0)[/latex]