Learning Outcome
- Identify and follow steps for graphing a linear inequality with two variables
So how do you get from the algebraic form of an inequality, like [latex]y>3x+1[/latex], to a graph of that inequality? Plotting inequalities is fairly straightforward if you follow a couple steps.
To graph an inequality:
- Graph the related boundary line. Replace the <, >, ≤ or ≥ sign in the inequality with = to find the equation of the boundary line.
- Identify at least one ordered pair on either side of the boundary line and substitute those [latex](x,y)[/latex] values into the inequality. Shade the region that contains the ordered pairs that make the inequality a true statement.
- If points on the boundary line are solutions, then use a solid line for drawing the boundary line. This will happen for ≤ or ≥ inequalities.
- If points on the boundary line are not solutions, then use a dotted line for the boundary line. This will happen for < or > inequalities.
Graph the inequality [latex]x+4y\leq4[/latex].
To graph the boundary line, find at least two values that lie on the line [latex]x+4y=4[/latex]. You can use the x and y-intercepts for this equation by substituting [latex]0[/latex] in for x first and finding the value of y; then substitute [latex]0[/latex] in for y and find x.
| x | y |
| [latex]0[/latex] | [latex]1[/latex] |
| [latex]4[/latex] | [latex]0[/latex] |
Plot the points [latex](0,1)[/latex] and [latex](4,0)[/latex], and draw a line through these two points for the boundary line. The line is solid because ≤ means “less than or equal to,” so all ordered pairs along the line are included in the solution set.
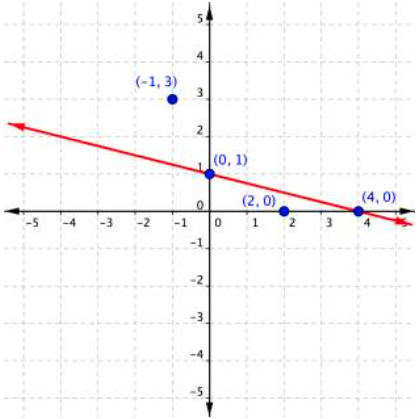
The next step is to find the region that contains the solutions. Is it above or below the boundary line? To identify the region where the inequality holds true, you can test a couple of ordered pairs, one on each side of the boundary line.
If you substitute [latex](−1,3)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}−1+4\left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]
This is a false statement since [latex]11[/latex] is not less than or equal to [latex]4[/latex].
On the other hand, if you substitute [latex](2,0)[/latex] into [latex]x+4y\leq4[/latex]:
[latex]\begin{array}{r}2+4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{array}[/latex]
This is true! The region that includes [latex](2,0)[/latex] should be shaded, as this is the region of solutions for the inequality.
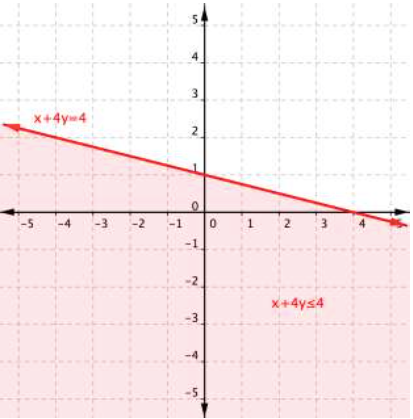
And there you have it, the graph of the set of solutions for [latex]x+4y\leq4[/latex].
Below is a video about how to graph inequalities with two variables.
Example
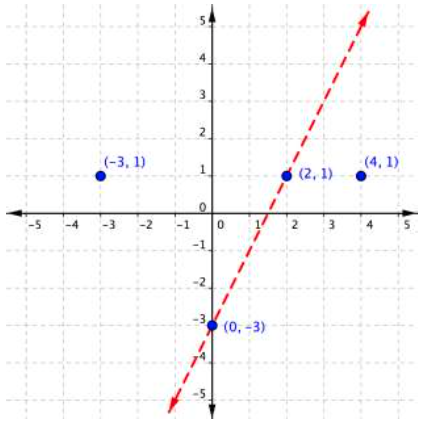
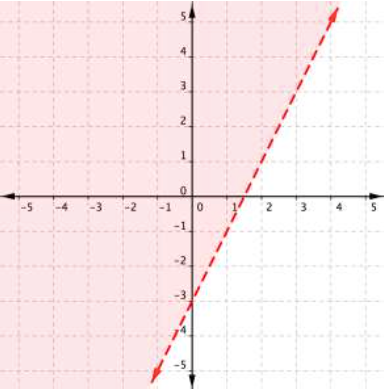
Graph the inequality [latex]2y>4x–6[/latex].
A quick note about the problem above: notice that you can use the points [latex](0,−3)[/latex] and [latex](2,1)[/latex] to graph the boundary line, but these points are not included in the region of solutions since the region does not include the boundary line!
Below is a video about how to graph inequalities with two variables when the equation is in what is known as slope-intercept form.
Summary
When inequalities are graphed on a coordinate plane, the solutions are located in a region of the coordinate plane which is represented as a shaded area on the plane. The boundary line for the inequality is drawn as a solid line if the points on the line itself do satisfy the inequality, as in the cases of ≤ and ≥. It is drawn as a dashed line if the points on the line do not satisfy the inequality, as in the cases of < and >. You can tell which region to shade by testing some points in the inequality. Using a coordinate plane is especially helpful for visualizing the region of solutions for inequalities with two variables.