We have seen two outcomes for solutions to quadratic equations; either there was one or two real number solutions. We have also learned that it is possible to take the square root of a negative number by using imaginary numbers. Having this new knowledge allows us to explore one more possible outcome when we solve quadratic equations. Consider this equation:

[latex]2x^2+3x+6=0[/latex]

Using the Quadratic Formula to solve this equation, we first identify a, b, and c.

[latex]a = 2,b = 3,c = 6[/latex]

We can place a, b and c into the quadratic formula and simplify to get the following result:

[latex]x=-\frac{3}{4}+\frac{\sqrt{-39}}{4}, x=-\frac{3}{4}-\frac{\sqrt{-39}}{4}[/latex]

Up to this point, we would have said that [latex]\sqrt{-39}[/latex] is not defined for real numbers and determine that this equation has no solutions.  But, now that we have defined the square root of a negative number, we can also define a solution to this equation as follows.

[latex]x=-\frac{3}{4}+i\frac{\sqrt{39}}{4}, x=-\frac{3}{4}-i\frac{\sqrt{39}}{4}[/latex]

In this section we will practice simplifying and writing solutions to quadratic equations that are complex.  We will then present a technique for classifying whether the solution(s) to a quadratic equation will be complex, and how many solutions there will be.

In our first example, we will work through the process of solving a quadratic equation with complex solutions. Take note that we will be simplifying complex numbers, so if you need a review of how to rewrite the square root of a negative number as an imaginary number, now is a good time.

We can check these solutions in the original equation. Be careful when you expand the squares, and replace [latex]i^{2}[/latex] with [latex]-1[/latex].

Now that we have had a little practice solving quadratic equations whose solutions are complex, we can explore a related feature of quadratic functions. Consider the following function: [latex]f(x)=x^2+2x+3[/latex].  Recall that the x-intercepts of a function are found by setting the function equal to zero:

[latex]x^2+2x+3=0[/latex]

The function now looks like the type of quadratic equations we have been solving. In the next example, we will solve this equation, then graph the original function and see that it has no x-intercepts.

Example

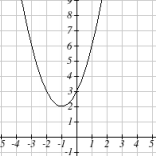
Find the x-intercepts of the quadratic function. [latex]f(x)=x^2+2x+3[/latex]

Show Solution

The x-intercepts of the function [latex]f(x)=x^2+2x+3[/latex] are found by setting it equal to zero and solving for x since the y values of the x-intercepts are zero.

First, identify a, b, c.

[latex]\begin{array}{l}x^2+2x+3=0\\a=1,b=2,c=3\end{array}[/latex]

Substitute these values into the quadratic formula.

[latex]\begin{array}{ll}x & =\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a} \\ & =\frac{-2\pm \sqrt{{2}^{2}-4(1)(3)}}{2(1)} \\ & =\frac{-2\pm \sqrt{4-12}}{2} \\ & =\frac{-2\pm \sqrt{-8}}{2} \\ & =\frac{-2\pm 2i\sqrt{2}}{2} \\ & =-1\pm i\sqrt{2} \\ &=-1+i\sqrt{2},-1-i\sqrt{2}\end{array}[/latex]

The solutions to this equations are complex, therefore there are no x-intercepts for the function [latex]f(x)=x^2+2x+3[/latex] in the set of real numbers that can be plotted on the Cartesian Coordinate plane. The graph of the function is plotted on the Cartesian Coordinate plane below:

Graph of quadratic function with no x-intercepts in the real numbers.

Note how the graph does not cross the x-axis; therefore, there are no real x-intercepts for this function.

The following video gives another example of how to use the quadratic formula to find solutions to a quadratic equation that has complex solutions.

Summary

Quadratic equations can have complex solutions. Quadratic functions whose graphs do not cross the x-axis will have complex solutions for [latex]f(x)=0[/latex].