Graphing a Linear Function Using Transformations

Another option for graphing linear functions is to use transformations of the identity function [latex]f\left(x\right)=x[/latex] . A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.

Vertical Stretch or Compression

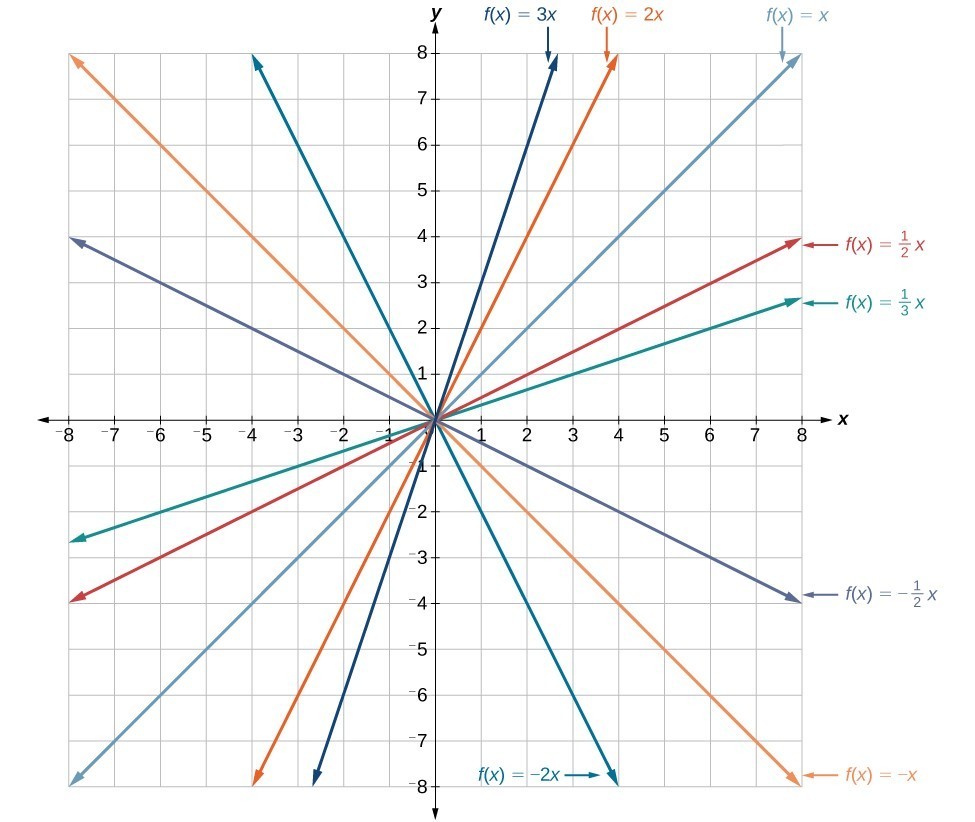
In the equation [latex]f\left(x\right)=mx[/latex], the m is acting as the vertical stretch or compression of the identity function. When m is negative, there is also a vertical reflection of the graph. Notice in the figure below that multiplying the equation of [latex]f\left(x\right)=x[/latex] by m vertically stretches the graph of f by a factor of m units if [latex]m>1[/latex] and vertically compresses the graph of f by a factor of m units if [latex]0<m<1[/latex]. This means the larger the absolute value of m, the steeper the slope. Below you can see a variety of vertical stretches, compressions, and/or reflections on the function [latex]f\left(x\right)=x[/latex].

Vertical Shift

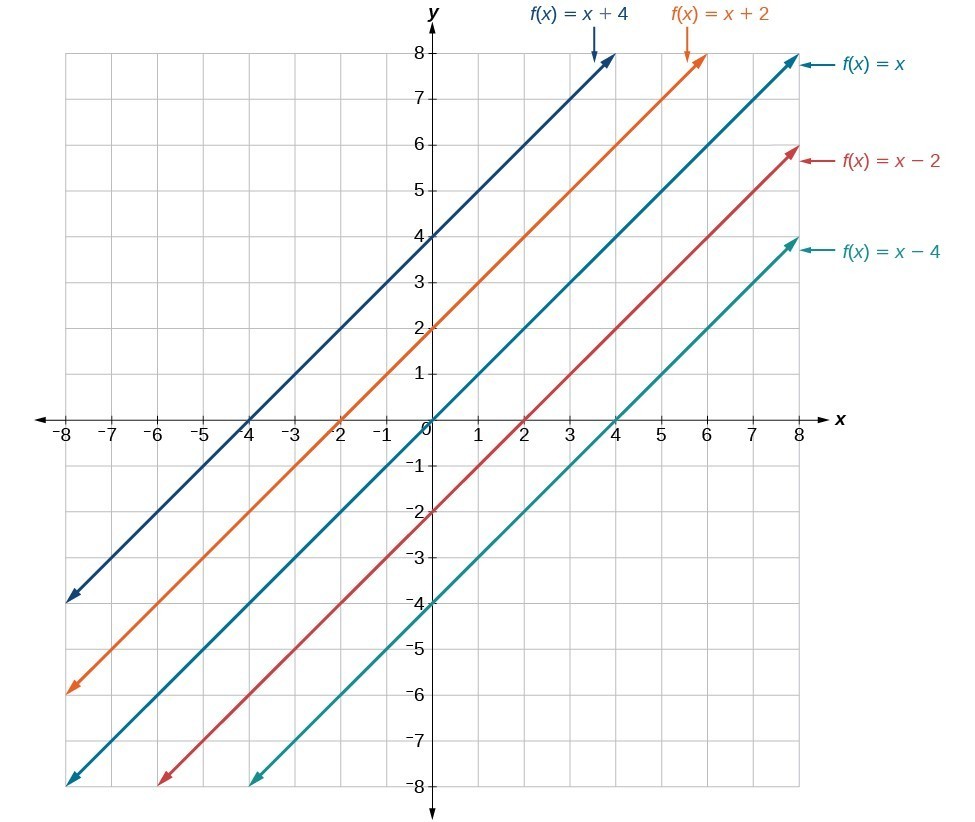
In [latex]f\left(x\right)=mx+b[/latex], the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice in the figure below that adding a value of b to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of f a total of b units up if b is positive and [latex]|b|[/latex] units down if b is negative. The graph below illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].

Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.

In the first example, we will see how a vertical compression changes the graph of the identity function.

Example

Describe the transformations to the function [latex]f(x)=\dfrac{2}{3}x[/latex] and draw a graph.

Show Solution

In this case, [latex]m=\dfrac{2}{3}[/latex], so this is a vertical compression since [latex]0<m<1[/latex].

The graph of [latex]f(x)=\dfrac{2}{3}x[/latex] is plotted below with the identity:

Note how the identity is compressed because the rate of change is “slowed” due to the vertical compression of [latex]\dfrac{2}{3}[/latex]

In the next example we will vertically stretch the identity by a factor of [latex]2[/latex].

Example

Describe the transformations to the function [latex]f(x)=2x[/latex] and draw a graph.

Show Solution

In this case, [latex]m=2[/latex], so this is a vertical stretch since [latex]m>1[/latex].

The graph of [latex]f(x)=2x[/latex] is plotted below with the identity:

y=2x and y=x

Note how the identity is more steep because the rate of change is “faster” due to the vertical stretch of [latex]2[/latex]

Our next example shows how making the slope negative reflects the identity across the y-axis.

Example

Describe the transformations to the function [latex]f(x)=-2x[/latex] and draw a graph.

Show Solution

In this case, [latex]m=-2[/latex], so this is a vertical stretch since [latex]|m|>1[/latex]. The negative sign reflects the graph across the y-axis.

The graph of [latex]f(x)=-2x[/latex] is plotted below with the identity:

y = x and y = -2x

Note how the steepness of the graph of  [latex]f(x)=-2x[/latex] is similar to[latex]f(x)=2x[/latex] but it points in the opposite direction because of the negative.

In our last example, we will combine a vertical compression and a vertical shift to transform [latex]f(x)=x[/latex] into [latex]f\left(x\right)=\dfrac{1}{2}x - 3[/latex] and draw the graph.

Example

Graph [latex]f\left(x\right)=\dfrac{1}{2}x - 3[/latex] using transformations.

Show Solution

The equation for the function shows that [latex]m=\dfrac{1}{2}[/latex], so the identity function is vertically compressed by [latex]\dfrac{1}{2}[/latex]. The equation for the function also shows that [latex]b=–3[/latex], so the identity function is vertically shifted down [latex]3[/latex] units. First, graph the identity function and show the vertical compression. Below is the function [latex]y=x[/latex], compressed by a factor of [latex]\dfrac{1}{2}[/latex].

Now show the vertical shift. The function [latex]y=\dfrac{1}{2}x[/latex] shifted down [latex]3[/latex] units is shown below.

The following video example describes another linear transformation of the identity and its corresponding graph.

Summary

• Vertical compressions of the identity happen when the slope is between [latex]0[/latex] and [latex]1[/latex].
• Vertical stretches of the identity happen when the slope is greater than [latex]1[/latex].
• Reflections happen when the slope is negative.
• Vertical shifts happen when the intercept is not equal to [latex]0[/latex].
• Multiple transformations can be made to a function.