Point-Slope Form

We have seen that we can define the slope of a line given two points on the line and use that information along with the y-intercept to graph the line.  If you do not know the y-intercept or the equation for the line, you can use two points to define the equation of the line using point-slope form.

[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]

This is an important formula, as it will be used in other algebra courses and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.

In our first example, we will start with the slope. Then, we will show how to find the equation of a line when the slope is not given.

In our next example, we will start with two points and find the equation of the line that passes through them.

The following video shows how to write the equation for a line given its slope and a point on the line.

Standard Form of a Line

Another way that we can represent the equation of a line is in standard form. Standard form is given as

[latex]Ax+By=C[/latex]

where [latex]A[/latex], [latex]B[/latex], and [latex]C[/latex] are integers. The x and y terms are on one side of the equal sign, and the constant term is on the other side.

Vertical and Horizontal Lines

The equations of vertical and horizontal lines do not require any of the preceding formulas although we can use the formulas to prove that the equations are correct. The equation of a vertical line is given as

[latex]x=c[/latex]

where c is a constant. The slope of a vertical line is undefined, and regardless of the y-value of any point on the line, the x-coordinate of the point will be c.

Suppose that we want to find the equation of a line containing the following points: [latex]\left(-3,-5\right),\left(-3,1\right),\left(-3,3\right)[/latex], and [latex]\left(-3,5\right)[/latex]. First, we will find the slope.

[latex]m=\dfrac{5 - 3}{-3-\left(-3\right)}=\dfrac{2}{0}[/latex]

Zero in the denominator means that the slope is undefined which makes using point-slope form impossible. However, we can plot the points. Notice that all of the x-coordinates are the same and we find a vertical line through [latex]x=-3[/latex].

The equation of a horizontal line is given as

[latex]y=c[/latex]

where c is a constant. The slope of a horizontal line is zero, and for any x-value of a point on the line, the corresponding y-coordinate will be c.

Suppose we want to find the equation of a line that contains the following set of points: [latex]\left(-2,-2\right),\left(0,-2\right),\left(3,-2\right)[/latex], and [latex]\left(5,-2\right)[/latex]. We can use point-slope form. First, we find the slope using any two points on the line.

[latex]\begin{array}{l}m & =\dfrac{-2-\left(-2\right)}{0-\left(-2\right)}\hfill \\ & =\dfrac{0}{2}\hfill \\ & =0\hfill \end{array}[/latex]

Use any point for [latex]\left({x}_{1},{y}_{1}\right)[/latex] in point-slope form.

[latex]\begin{array}{l}y-\left(-2\right)=0\left(x - 3\right)\hfill \\ y+2=0\hfill \\ y=-2\hfill \end{array}[/latex]

The graph is a horizontal line through [latex]y=-2[/latex]. Notice that all of the y-coordinates are the same.

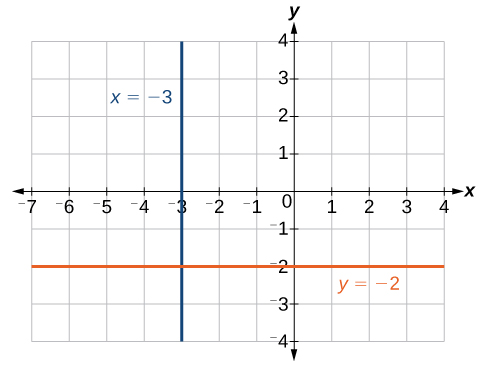
The line [latex]x=−3[/latex] is a vertical line. The line [latex]y=−2[/latex] is a horizontal line.

Our last video shows another example of writing the equation of a line given two points on the line.

Summary

• The slope of a line indicates the direction which it slants as well as its steepness. Slope is defined algebraically as:[latex]m=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
• Given the slope and one point on a line, we can find the equation of the line using point-slope form. [latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
• Standard form of a line is given as [latex]Ax+By=C[/latex]
• The equation of a vertical line is given as [latex]x=c[/latex]
• The equation of a horizontal line is given as [latex]y=c[/latex]