Learning Outcomes
- Define a one-to-one function
- Use the horizontal line test to determine whether a function is one-to-one
Remember that in a function, the input value must have one and only one value for the output. There is a name for the set of input values and another name for the set of output values for a function. The set of input values is called the domain of the function. The set of output values is called the range of the function.
In the first example, we remind you how to define domain and range using a table of values.
Example
Find the domain and range for the function.
| x | y |
|---|---|
| [latex]−5[/latex] | [latex]−6[/latex] |
| [latex]−2[/latex] | [latex]−1[/latex] |
| [latex]−1[/latex] | [latex]0[/latex] |
| [latex]0[/latex] | [latex]3[/latex] |
| [latex]5[/latex] | [latex]15[/latex] |
In the following video, we show another example of finding domain and range from tabular data.
Some functions have a given output value that corresponds to two or more input values. For example, in the following stock chart the stock price was [latex]$1000[/latex] on five different dates, meaning that there were five different input values that all resulted in the same output value of [latex]$1000[/latex].

However, some functions have only one input value for each output value as well as having only one output value for each input value. We call these functions one-to-one functions. As an example, consider a school that uses only letter grades and decimal equivalents as listed below.
| Letter grade | Grade point average |
|---|---|
| A | [latex]4.0[/latex] |
| B | [latex]3.0[/latex] |
| C | [latex]2.0[/latex] |
| D | [latex]1.0[/latex] |
This grading system represents a one-to-one function, because each letter input yields one particular grade point average output and each grade point average corresponds to one input letter.
To visualize this concept, let us look again at the two simple functions sketched in (a) and (b) below. Note that (c) is not a function since the input q produces two outputs, y and z.
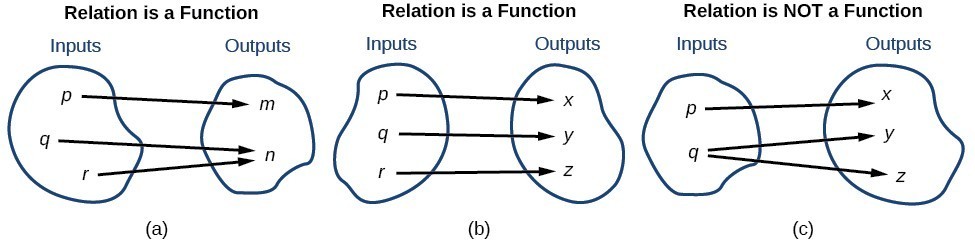
The function in part (a) shows a relationship that is not a one-to-one function because inputs [latex]q[/latex] and [latex]r[/latex] both give output [latex]n[/latex]. The function in part (b) shows a relationship that is a one-to-one function because each input is associated with a single output.
A General Note: One-to-One Function
A one-to-one function is a function in which each output value corresponds to exactly one input value.
Example
Determine whether each of the following tables represents a one-to-one function.
a)
| Input | Output |
| [latex]1[/latex] | [latex]5[/latex] |
| [latex]12[/latex] | [latex]2[/latex] |
| [latex]0[/latex] | [latex]-1[/latex] |
| [latex]4[/latex] | [latex]2[/latex] |
| [latex]-5[/latex] | [latex]0[/latex] |
b)
| Input | Output |
| [latex]4[/latex] | [latex]8[/latex] |
| [latex]8[/latex] | [latex]16[/latex] |
| [latex]16[/latex] | [latex]32[/latex] |
| [latex]32[/latex] | [latex]64[/latex] |
| [latex]64[/latex] | [latex]128[/latex] |
In the following video, we show an example of using tables of values to determine whether a function is one-to-one.
Using the Horizontal Line Test
An easy way to determine whether a function is a one-to-one function is to use the horizontal line test on the graph of the function. To do this, draw horizontal lines through the graph. If any horizontal line intersects the graph more than once, then the graph does not represent a one-to-one function.
How To: Given a graph of a function, use the horizontal line test to determine if the graph represents a one-to-one function
- Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
- If there is any such line, determine that the function is not one-to-one.
EXAMPLE
For the following graphs, determine which represent one-to-one functions.

The following video provides another example of using the horizontal line test to determine whether a graph represents a one-to-one function.
Summary
In real life and in algebra, different variables are often linked. When a change in value of one variable causes a change in the value of another variable, their interaction is called a relation. A relation has an input value which corresponds to an output value. When each input value has one and only one output value, the relation is a function. When each output value has one and only one input value, the function is one-to-one. Functions can be written as ordered pairs, tables, or graphs. The set of input values is called the domain, and the set of output values is called the range.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Determine if a Relation Given as a Table is a One-to-One Function. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/QFOJmevha_Y. License: CC BY: Attribution
- Ex 1: Use the Vertical Line Test to Determine if a Graph Represents a Function. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/5Z8DaZPJLKY. License: CC BY: Attribution
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution



