Tree and Venn Diagrams

Learning Outcomes

  • Construct and interpret Tree Diagrams
  • Construct and interpret Venn Diagrams

Sometimes, when the probability problems are complex, it can be helpful to graph the situation. Tree diagrams and Venn diagrams are two tools that can be used to visualize and solve conditional probabilities.

Tree Diagrams

A tree diagram is a special type of graph used to determine the outcomes of an experiment. It consists of “branches” that are labeled with either frequencies or probabilities. Tree diagrams can make some probability problems easier to visualize and solve. The following example illustrates how to use a tree diagram.

Example

In an urn, there are [latex]11[/latex] balls. Three balls are red ([latex]R[/latex]) and eight balls are blue ([latex]B[/latex]). Draw two balls, one at a time, with replacement. “With replacement” means that you put the first ball back in the urn before you select the second ball. The tree diagram using frequencies that show all the possible outcomes follows.

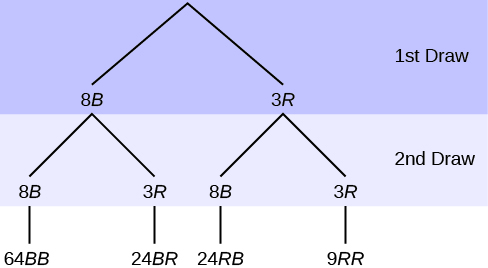
This is a tree diagram with branches showing frequencies of each draw. The first branch shows two lines: 8B and 3R. The second branch has a set of two lines (8B and 3R) for each line of the first branch. Multiply along each line to find 64BB, 24BR, 24RB, and 9RR.
Total = [latex]64 + 24 + 24 + 9 = 121[/latex]

The first set of branches represents the first draw. The second set of branches represents the second draw. Each of the outcomes is distinct. In fact, we can list each red ball as [latex]R1[/latex], [latex]R2[/latex], and [latex]R3[/latex] and each blue ball as [latex]B1[/latex], [latex]B2[/latex], [latex]B3[/latex], [latex]B4[/latex], [latex]B5[/latex], [latex]B6[/latex], [latex]B7[/latex], and [latex]B8[/latex]. Then the nine [latex]RR[/latex] outcomes can be written as:
[latex]R1R1;\,\, R1R2;\,\, R1R3;\,\, R2R1;\,\, R2R2;\,\, R2R3;\,\, R3R1;\,\, R3R2;\,\, R3R3[/latex]
The other outcomes are similar.

There are a total of [latex]11[/latex] balls in the urn. Draw two balls, one at a time, with replacement. There are [latex]11(11) = 121[/latex] outcomes, the size of the sample space.

  1. List the [latex]24[/latex] [latex]BR[/latex] outcomes: [latex]B1R1[/latex], [latex]B1R2[/latex], [latex]B1R3[/latex], …
  2. Using the tree diagram, calculate [latex]P(RR)[/latex].
  3. Using the tree diagram, calculate [latex]P(RB \text{ OR } BR)[/latex].
  4. Using the tree diagram, calculate [latex]P(R \text{ on 1st draw AND } B \text { on 2nd draw })[/latex].
  5. Using the tree diagram, calculate [latex]P(R \text{ on 2nd draw GIVEN } B \text { on 1st draw })[/latex].
  6. Using the tree diagram, calculate [latex]P(BB)[/latex].
  7. Using the tree diagram, calculate [latex]P(B \text{ on the 2nd draw given } R \text { on the first draw })[/latex].

Example

An urn has three red marbles and eight blue marbles in it. Draw two marbles, one at a time, this time without replacement, from the urn. “Without replacement” means that you do not put the first ball back before you select the second marble. Following is a tree diagram for this situation. The branches are labeled with probabilities instead of frequencies. The numbers at the ends of the branches are calculated by multiplying the numbers on the two corresponding branches, for example, [latex](\frac{3}{11})(\frac{2}{10})=(\frac{6}{110})[/latex].

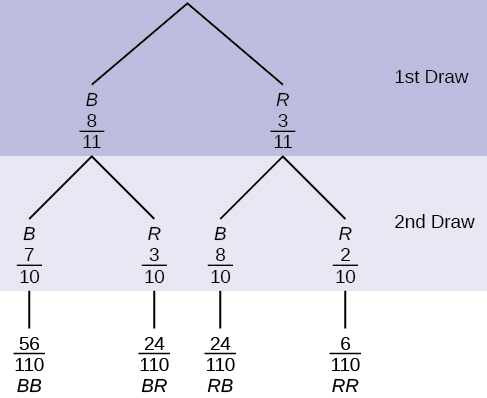
This is a tree diagram with branches showing probabilities of each draw. The first branch shows 2 lines: B 8/11 and R 3/11. The second branch has a set of 2 lines for each first branch line. Below B 8/11 are B 7/10 and R 3/10. Below R 3/11 are B 8/10 and R 2/10. Multiply along each line to find BB 56/110, BR 24/110, RB 24/110, and RR 6/110.
Total = [latex]\displaystyle\frac{{56+24+24+6}}{{110}}=\frac{{110}}{{110}}=1[/latex]

Note

If you draw a red on the first draw from the three red possibilities, there are two red marbles left to draw on the second draw. You do not put back or replace the first marble after you have drawn it. You draw without replacement, so that on the second draw there are ten marbles left in the urn.

Calculate the following probabilities using the tree diagram.

a. [latex]P(RR)[/latex] = ________

b. Fill in the blanks:
[latex]P(RB \text{ OR } BR = (\frac{3}{11})(\frac{8}{10}) + (\rule{1cm}{0.15mm})(\rule{1cm}{0.15mm}) = \frac{48}{110}[/latex]

c. [latex]P(R \text{ on 2nd|}B \text{ on 1st}) =[/latex]

 d. Fill in the blanks.

[latex]P(R \text{ on 1st AND } B \text{ on 2nd }) = P(RB) = (\rule{1cm}{0.15mm})(\rule{1cm}{0.15mm})= \frac{24}{110}[/latex]

e. Find [latex]P(BB)[/latex].

f. Find [latex]P(B \text{ on 2nd|}R \text{ on 1st})[/latex].

a. [latex]P(RR) = (\frac{3}{11})(\frac{2}{10}) = \frac{6}{110}[/latex]

b. [latex]P(RB \text{ OR } BR = (\frac{3}{11})(\frac{8}{10}) + (\frac{8}{11})(\frac{3}{10}) = \frac{48}{110}[/latex]

c. [latex]P(R \text{ on 2nd|}B \text{ on 1st }) =\frac{3}{10}[/latex]

d. [latex]P(R \text{ on 1st AND } B \text{ on 2nd }) = P(RB) = (\frac{3}{11})(\frac{8}{10})= \frac{24}{110}[/latex]

e. [latex]P(BB) = (\frac{8}{11})(\frac{7}{10})[/latex]

f. Using the tree diagram, [latex]P(B \text{ on 2nd|}R \text{ on 1st }) = P(R|B) = (\frac{8}{10})[/latex]

If we are using probabilities, we can label the tree in the following general way.

This is a tree diagram for a two-step experiment. The first branch shows first outcome: P(B) and P(R). The second branch has a set of 2 lines for each line of the first branch: the probability of B given B = P(BB), the probability of R given B = P(RB), the probability of B given R = P(BR), and the probability of R given R = P(RR).

  • [latex]P(RR)[/latex] here means [latex]P(R \text{ on 2nd|}R \text{ on 1st})[/latex]
  • [latex]P(BR)[/latex] here means [latex]P(B \text{ on 2nd|}R \text{ on 1st})[/latex]
  • [latex]P(RB)[/latex] here means [latex]P(R \text{ on 2nd|}B \text{ on 1st})[/latex]
  • [latex]P(BB)[/latex] here means [latex]P(B \text{ on 2nd|}B \text{ on 1st})[/latex]

Venn Diagram

A Venn diagram is a picture that represents the outcomes of an experiment. It generally consists of a box that represents the sample space S together with circles or ovals. The circles or ovals represent events.

Example

Suppose an experiment has the outcomes [latex]1, 2, 3, ... , 12[/latex] where each outcome has an equal chance of occurring. Let event [latex]A = \{1, 2, 3, 4, 5, 6\}[/latex] and event [latex]B = \{6, 7, 8, 9\}[/latex]. Then [latex]A \text{ AND } B = \{6\}[/latex] and [latex]A \text{ OR }B = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}[/latex]. The Venn diagram is as follows:

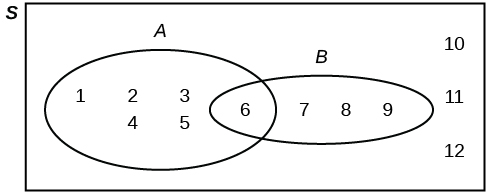
A Venn diagram. An oval representing set A contains the values 1, 2, 3, 4, 5, and 6. An oval representing set B also contains the 6, along with 7, 8, and 9. The values 10, 11, and 12 are present but not contained in either set.

 

Example

Flip two fair coins. Let [latex]A[/latex] = tails on the first coin. Let [latex]B[/latex] = tails on the second coin. Then [latex]A = \{TT, TH\}[/latex] and [latex]B = \{TT, HT\}[/latex]. Therefore,[latex]A \text{ AND } B = \{TT\}[/latex]. [latex]A \text{ OR } B = \{TH, TT, HT\}[/latex].

The sample space when you flip two fair coins is [latex]X = \{HH, HT, TH, TT\}[/latex]. The outcome [latex]HH[/latex] is in NEITHER [latex]A[/latex] NOR [latex]B[/latex]. The Venn diagram is as follows:

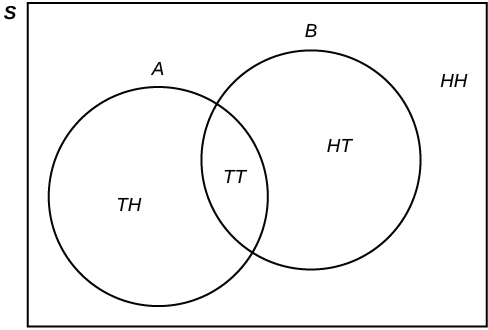
This is a venn diagram. An oval representing set A contains Tails + Heads and Tails + Tails. An oval representing set B also contains Tails + Tails, along with Heads + Tails. The universe S contains Heads + Heads, but this value is not contained in either set A or B.

 

Glossary

Tree Diagram
the useful visual representation of a sample space and events in the form of a “tree” with branches marked by possible outcomes together with associated probabilities (frequencies, relative frequencies)
Venn Diagram
the visual representation of a sample space and events in the form of circles or ovals showing their intersections
Solutions to Try These 1:
a.
B1R1 B1R2 B1R3 B2R1 B2R2 B2R3 B3R1 B3R2 B3R3 B4R1 B4R2 B4R3 B5R1 B5R2 B5R3 B6R1 B6R2 B6R3 B7R1B7R2 B7R3 B8R1 B8R2 B8R3
b. P(RR) = (311)(311) = 9121
c. P(RB OR BR) = (311)(811) + (811)(311) = 48121
d. P(R on 1st draw AND B on 2nd draw) = P(RB) = (311)(811) = 24121

e. P(R on 2nd draw GIVEN B on 1st draw) = P(R on 2nd|B on 1st) = 2488 = 311

This problem is a conditional one. The sample space has been reduced to those outcomes that already have a blue on the first draw. There are 24 + 64 = 88 possible outcomes (24 BR and 64 BB). Twenty-four of the 88 possible outcomes are BR. 2488 = 311.

f. P(BB) = 64121

g. P(B on 2nd draw|R on 1st draw) = 811

There are 9 + 24 outcomes that have R on the first draw (9 RR and 24 RB). The sample space is then 9 + 24 = 33. 24 of the 33 outcomes have B on the second draw. The probability is then 2433.

Solutions to Try These 2:

a. P(RR) = (311)(210)=6110
b. P(RB OR BR) = (311)(810) + (811)(310) = 48110
c. P(R on 2nd|B on 1st) = 310
d. P(R on 1st AND B on 2nd) = P(RB) = (311)(810) = 24100
e. P(BB) = (811)(710)
f. Using the tree diagram, P(B on 2nd|R on 1st) = P(R|B) = 810.