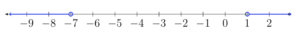Absolute Value Equations and Inequalities

Learning Objectives

Evaluate expressions that contain absolute value
Solve absolute value equations
Solve absolute value inequalities

We saw that numbers such as $5$ and $-5$ are opposites because they are the same distance from $0$ on the number line. They are both five units from $0$ . The distance between $0$ and any number on the number line is called the absolute value of that number.

Because distance is never negative, the absolute value of any number is never negative.

The symbol for absolute value is two vertical lines on either side of a number. So the absolute value of $5$ is written as $|5|$ , and the absolute value of $-5$ is written as $|-5|$ as shown below.

This figure is a number line. The points negative 5 and 5 are labeled. Above the number line the distance from negative 5 to 0 is labeled as 5 units. Also above the number line the distance from 0 to 5 is labeled as 5 units.

Absolute Value

The absolute value of a number is its distance from $0$ on the number line.
The absolute value of a number $n$ is written as $|n|$ .

$|n|\ge 0$ for all numbers

Simplify:

$|3|$
$|-44|$
$|0|$

Show Answer

1.
	$\|3\|$
$3$ is $3$ units from zero.	$3$

2.
	$\|-44\|$
$−44$ is $44$ units from zero.	$44$

3.
	$\|0\|$
$0$ is already at zero.	$0$

In the video below we show another example of how to find the absolute value of an integer.

Solve Equations Containing Absolute Value

When solving absolute value equations, we are asking about when the distance of an expression from $0$ is a particular value. Because both positive and negative values have a positive absolute value, solving absolute value equations means finding the solution for both the positive and the negative values.

Consider the equation $|x|=5$ . This equation asks you to find all numbers whose distance is $5$ units from $0$ . Its solutions are $5$ and $-5$ .

Solving Equations of the Form $|x|=a$

For any positive number $a$ , the solution of $\left|x\right|=a$ is

$x=a$ or $x=−a$

$x$ can be a single variable or any algebraic expression.

You can solve a more complex absolute value problem in a similar fashion.

Example

Solve $\displaystyle \left| x+5\right|=15$ .

Show Solution

This equation asks you to find what number plus $5$ has an absolute value of $15$ . Since $15$ and $−15$ both have an absolute value of $15$ , the absolute value equation is true when the quantity $x + 5$ is $15$ or $x + 5$ is $−15$ , since $|15|=15$ and $|−15|=15$ . So, you need to find out what value for $x$ will make this expression equal to $15$ , as well as what value for $x$ will make the expression equal to $−15$ . Solving the two equations you get

$\displaystyle \begin{array}{l}x+5=15\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,{x+5=-15}\\\underline{\,\,\,\,\,-5\,\,\,\,-5}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-5\,\,\,\,\,\,\,\,\,-5}\\x\,\,\,\,\,\,\,\,\,=\,\,10\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,=-20\end{array}$

You can check these two solutions in the absolute value equation to see if $x=10$ and $x = −20$ are correct.

$\displaystyle \begin{array}{r}\,\,\left| x+5 \right|=15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+5 \right|=15\\\left| 10+5 \right|=15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -20+5 \right|=15\\\,\,\,\,\,\,\,\left| 15 \right|=15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -15 \right|=15\\\,\,\,\,\,\,\,\,\,15=15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,15=15\end{array}$

The following video provides worked examples of solving linear equations with absolute value terms.

Now we will see how to solve equations with absolute value that include multiplication.

Example

Solve $\displaystyle \left| 2x\right|=6$ .

Show Solution

This equation asks you to find what number times $2$ has an absolute value of $6$ .

Since $6$ and $−6$ both have an absolute value of $6$ , the absolute value equation is true when the quantity $2x$ is $6$ or $2x$ is $−6$ , since $|6|=6$ and $|−6|=6$ .

So, you need to find out what value for $x$ will make this expression equal to $6$ , as well as what value for $x$ will make the expression equal to $−6$ .

Solving the two equations you get

$2x=6\text { or } 2x=-6$

$\frac{2x}{2}=\frac{6}{2}\text { or } \frac{2x}{2}=\frac{-6}{2}$

$x=3\text { or } x=-3$

You can check these two solutions in the absolute value equation to see if $x=3$ and $x=−3$ are correct.

$\displaystyle \begin{array}{r}\,\,\left|3\cdot2 \right|=6\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -3\cdot2 \right|=6\\\left| 6 \right|=6\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| -6 \right|=6\\\end{array}$

In the following video, you will see two examples of how to solve an absolute value equation, one with integers and one with fractions.

Sometimes an absolute value equation has no solution. For example, $|x| = -2$ has no solution since the absolute value of a number is never negative.

Solve Inequalities Containing Absolute Value

Let us apply what you know about solving equations that contain absolute value and what you know about inequalities to solve inequalities that contain absolute value. Let us start with a simple inequality.

$\left|x\right|\leq 4$

This inequality is read, “the absolute value of x is less than or equal to $4$ .” If you are asked to solve for x, you want to find out what values of x are $4$ units or less away from $0$ on a number line. You could start by thinking about the number line and what values of x would satisfy this equation.

$4$ and $−4$ are both four units away from $0$ , so they are solutions. $3$ and $−3$ are also solutions because each of these values is less than $4$ units away from $0$ . So are $1$ and $−1$ , $0.5$ and $−0.5$ , and so on—there are an infinite number of values for x that will satisfy this inequality.

The graph of this inequality will have two closed circles, at $4$ and $−4$ . The distance between these two values on the number line is colored in blue because all of these values satisfy the inequality.

Number line. Closed blue circles on negative 4 and 4. Blue line between closed blue circles.

The solution can be written this way:

Inequality notation: $-4\leq x\leq4$

Interval notation: $\left[-4,4\right]$

The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.” Consider the simple inequality $\left|x\right|>3$ . Again, you could think of the number line and what values of x are greater than $3$ units away from zero. This time, $3$ and $−3$ are not included in the solution, so there are open circles on both of these values. $2$ and $−2$ would not be solutions because they are not more than $3$ units away from $0$ . But $5$ and $−5$ would work, and so would all of the values extending to the left of $−3$ and to the right of $3$ . The graph would look like the one below.

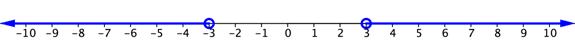
Number line. Open blue circles on negative three and three. Blue arrow through all numbers less than negative 3. Blue arrow through all numbers greater than 3.

The solution to this inequality can be written this way:

Inequality notation: $x<−3$ or $x>3$ .

Interval notation: $\left(-\infty, -3\right)\cup\left(3,\infty\right)$

For any positive value of a and x, a single variable, or any algebraic expression:

Absolute Value Inequality	Equivalent Inequality	Interval Notation
$\left\|{ x }\right\|\le{ a}$	${ -a}\le{x}\le{ a}$	$\left[-a, a\right]$
$\left\| x \right\|\lt{a}$	${ -a}\lt{x}\lt{ a}$	$\left(-a, a\right)$
$\left\| x \right\|\ge{ a}$	${x}\le\text{−a}$ or ${x}\ge{ a}$	$\left(-\infty,-a\right]\cup\left[a,\infty\right)$
$\left\| x \right\|\gt\text{a}$	$\displaystyle{x}\lt\text{−a}$ or ${x}\gt{ a}$	$\left(-\infty,-a\right)\cup\left(a,\infty\right)$

Let’s look at another example.

Example

Solve for $x$ : $\left|x+3\right|\gt4$

Show Solution

Since this is a “greater than” inequality, the solution can be rewritten according to the “greater than” rule.

$\displaystyle x+3<-4\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,\,x+3>4$

Solve each inequality.

$\begin{array}{r}x+3<-4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x+3>4\\\underline{\,\,\,\,-3\,\,\,\,\,-3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\,\,\,\,\,\,-3\,\,-3}\\x\,\,\,\,\,\,\,\,\,<-7\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x\,\,\,\,\,\,\,\,\,>1\\\\x<-7\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\,x>1\,\,\,\,\,\,\,\end{array}$

Check the solutions in the original equation to be sure they work. Check the end point of the first related equation, $−7$ and the end point of the second related equation, 1.

$\displaystyle \begin{array}{r}\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -7+3 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 1+3 \right|=4\\\,\,\,\,\,\,\,\left| -4 \right|=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 4 \right|=4\\\,\,\,\,\,\,\,\,\,\,\,\,4=4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4=4\end{array}$

Try $−10$ , a value less than $−7$ , and 5, a value greater than 1, to check the inequality.

$\displaystyle \begin{array}{r}\,\,\,\,\,\left| x+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| x+3 \right|>4\\\left| -10+3 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 5+3 \right|>4\\\,\,\,\,\,\,\,\,\,\,\left| -7 \right|>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| 8 \right|>4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,7>4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,8>4\end{array}$

Both solutions check!

Inequality notation: $\displaystyle x<-7\,\,\,\,\,\text{or}\,\,\,\,\,x>1$

Interval notation: $\left(-\infty, -7\right)\cup\left(1,\infty\right)$

Graph:

x is less than negative 7 or x is greater than 1 on a number line. An arrow begins with an open dot on negative 7 and extends to the left. An arrow begins with an open dot on 1 and extends to the right.

Caution: One difference between solving an equation and solving an inequality, is that if we multiply or divide both sides by a negative number, the sense of the inequality is reversed. For example, $-1 < 3$ . Suppose we multiply each of these numbers by $-2$ . $(-2)(-1)=2$ , and $(-2)(3)=-6$ . Now we have $2 > -6$ .

Module 6: Normal Distribution

Learning Objectives

Absolute Value

Solve Equations Containing Absolute Value

Solving Equations of the Form $|x|=a$

Example

Example

Solve Inequalities Containing Absolute Value

Example

Candela Citations

Module 6: Normal Distribution