Answers to Selected Exercises

Two Population Means with Unknown Standard Deviations – Practice

1. two proportions

3. matched or paired samples

5. single. mean

7. independent group means, population standard deviations and/or variances unknown

9. two proportions

11. independent group means, population standard deviations and/or variances unknown

13. independent group means, population standard deviations and/or variances unknown

15. two proportions

17. The random variable is the difference between the mean amounts of sugar in the two soft drinks.

19. means

21. two-tailed

23. the difference between the mean life spans of Whites and non-Whites

25. This is a comparison of two population means with unknown population standard deviations.

27. Check student’s solution

29.

Reject the null hypothesis
p-value < 0.05
There is not enough evidence at the 5% level of significance to support the claim that life expectancy in the 1900s is different between Whites and non-Whites.

Two Population Means with Known Standard Deviations – Practice

31. The difference in mean speeds of the fastball pitches of the two pitchers

33. –2.46

45. At the 1% significance level, we can reject the null hypothesis. There is sufficient data to conclude that the mean speed of Rodriguez’s fastball is faster than Wesley’s.

37. Subscripts: 1 = Food, 2 = No Food

H₀: μ₁ ≤ μ₂
H_a: μ₁ > μ₂

39.

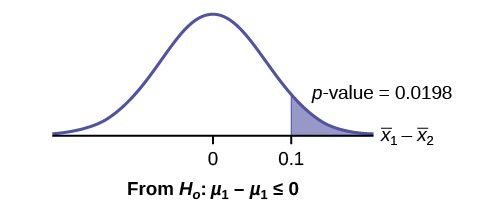
This is a normal distribution curve with mean equal to zero. The values 0 and 0.1 are labeled on the horiztonal axis. A vertical line extends from 0.1 to the curve. The region under the curve to the right of the line is shaded to represent p-value = 0.0198.

41. Subscripts: 1 = Gamma, 2 = Zeta

H₀: μ₁ = μ₂
H_a: μ₁ ≠ μ₂

43. 0.0062

45. There is sufficient evidence to reject the null hypothesis. The data support that the melting point for Alloy Zeta is different from the melting point of Alloy Gamma.

Comparing Two Independent Population Proportions – Practice

47. P′_OS1 – P′_OS2 = difference in the proportions of phones that had system failures within the first eight hours of operation with OS₁ and OS₂.

49. 0.1018

51. proportions

53. right-tailed

55. The random variable is the difference in proportions (percents) of the populations that are of two or more races in Nevada and North Dakota.

57. Our sample sizes are much greater than five each, so we use the normal for two proportions distribution for this hypothesis test.

59. Check student’s solution

61.

Reject the null hypothesis.
p-value < alpha
At the 5% significance level, there is sufficient evidence to conclude that the proportion (percent) of the population that is of two or more races in Nevada is statistically higher than that in North Dakota.

Matched or Paired Samples – Practice

63. the mean difference of the system failures

65. 0.0067

67. With a p-value of 0.0067, we can reject the null hypothesis. There is enough evidence to support that the software patch is effective in reducing the number of system failures.

69. 0.0021

71.

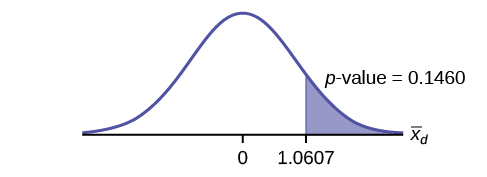
This is a normal distribution curve with mean equal to zero. The values 0 and 1.67 are labeled on the horiztonal axis. A vertical line extends from 1.67 to the curve. The region under the curve to the right of the line is shaded to represent p-value = 0.0021.

73.

H₀: μ_d ≥ 0
H_a: μ_d < 0

75. 0.0699

77. We decline to reject the null hypothesis. There is not sufficient evidence to support that the medication is effective.

Two Population Means with Unknown Standard Deviations – Homework

79. Subscripts: 1: two-year colleges; 2: four-year colleges

H₀: μ₁ ≥ μ₂
H_a: μ₁ < μ₂
[latex]\overline{X}_{1}–\overline{X}_{2}[/latex]is the difference between the mean enrollments of the two-year colleges and the four-year colleges.
Student’s t
test statistic: -0.2480
p-value: 0.4019
Check student’s solution.
1. Alpha: 0.05
2. Decision: Do not reject
3. Reason for Decision: p-value > alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean enrollment at four-year colleges is higher than at two-year colleges.

81. Subscripts: 1: mechanical engineering; 2: electrical engineering

H₀: µ₁ ≥ µ₂
H_a: µ₁ < µ₂
[latex]\overline{X}_{1}–\overline{X}_{2}[/latex] is the difference between the mean entry-level salaries of mechanical engineers and electrical engineers.
t₁₀₈
test statistic: t = –0.82
p-value: 0.2061
Check student’s solution.
1. Alpha: 0.05
2. Decision: Do not reject the null hypothesis.
3. Reason for Decision: p-value > alpha
4. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the mean entry-level salaries of mechanical engineers is lower than that of electrical engineers.

83.

H₀: µ₁ = µ₂
H_a: µ₁ ≠ µ₂
[latex]\overline{X}_{1}–\overline{X}_{2}[/latex] is the difference between the mean times for completing a lap in races and in practices.
t_20.32
test statistic: –4.70
p-value: 0.0001
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for Decision: p-value < alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean time for completing a lap in races is different from that in practices.

85.

H₀: µ₁ = µ₂
H_a: µ₁ ≠ µ₂
[latex]\overline{X}_{1}–\overline{X}_{2}[/latex] is the difference between the mean times for completing a lap in races and in practices.
t_40.94
test statistic: –5.08
p-value: zero
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for Decision: p-value < alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean time for completing a lap in races is different from that in practices.

88. There is insufficient evidence to conclude that the W teams score fewer goals, on average, than the E teams score.

90. Test: two independent sample means, population standard deviations unknown. [latex]\mu_1 =[/latex] the mean price of a sociology text on the selected site. [latex]\mu_2 =[/latex] the mean price of a math/science text on the selected site. Random variable: [latex]\overline{X_1} - \overline{X_1} =[/latex] the difference in the sample mean textbook price between sociology texts and math/science texts. Hypotheses: [latex]H_o : \mu_1 - \mu_2 = 0, H_a : \mu_2 < \mu_2 [/latex] which can be expressed as HOs: [latex]\mu 1 - \mu 2 , Ha \mu 1 < \mu 2[/latex]. Distribution for the test: Use [latex]t_{df}[/latex]; because each sample has more than 30 observations, [latex]df = n_1 + n_2 - 2 = 33+33-2=64[/latex]. Estimate the critical value on the $t$ -table using the nearest available degrees of freedom, 60. The critical value, 2.660, is found in the .0005 column.
Calculate the test statistic: [latex]t_c = \frac{(\overline{X_1} - \overline{X_2})-0}{\sqrt{\frac{s_1 ^2}{n_2} + \frac{s_2 ^2}{n_2}}} = \frac{(74.64-111.56)-0}{\sqrt{\frac{49.36^2}{33} + \frac{66.90^2}{33}}} = -2.55. Using a calculator with [latex]t_c = -2.555[/latex] and [latex]df=64[/latex], the left-tailed $p$ -value: Decision: Reject [latex]H_o[/latex]. Conclusion: At the 1% level of significance, from the sample data, there is sufficient evidence to conclude that the mean price of sociology textbooks is less than the mean price of textbooks for math/science.

92. μ_day ≠ μ_night

Two Population Means with Known Standard Deviations – Homework

94.

Subscripts: 1 = boys, 2 = girls

H₀: µ₁ ≤ µ₂
H_a: µ₁ > µ₂
The random variable is the difference in the mean auto insurance costs for boys and girls.
normal
test statistic: z = 2.50
p-value: 0.0062
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for Decision: p-value < alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean cost of auto insurance for teenage boys is greater than that for girls.

96.

Subscripts: 1 = non-hybrid sedans, 2 = hybrid sedans

H₀: µ₁ ≥ µ₂
H_a: µ₁ < µ₂
The random variable is the difference in the mean miles per gallon of non-hybrid sedans and hybrid sedans.
normal
test statistic: 6.36
p-value: 0
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for decision: p-value < alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the mean miles per gallon of non-hybrid sedans is less than that of hybrid sedans.

98.

H₀: µ_d = 0
H_a: µ_d < 0
The random variable X_d is the average difference between husband’s and wife’s satisfaction level.
t₉
test statistic: t = –1.86
p-value: 0.0479
Check student’s solution
1. Alpha: 0.05
2. Decision: Reject the null hypothesis, but run another test.
3. Reason for Decision: p-value < alpha
4. Conclusion: This is a weak test because alpha and the p-value are close. However, there is insufficient evidence to conclude that the mean difference is negative.

Comparing Two Independent Population Proportions – Homework

100.

H₀: P_W = P_BH_a: P_W ≠ P_BThe random variable is the difference in the proportions of White and Black suicide victims, aged 15 to 24. Normal for two proportions test statistic: –0.1944p-value: 0.8458 Check student’s solution.

Alpha: 0.05
Decision: Reject the null hypothesis.
Reason for decision: p-value > alpha
Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportions of White and Black female suicide victims, aged 15 to 24, are different.

102.

Subscripts: 1 = Cabrillo College, 2 = Lake Tahoe College

H₀: p₁ = p₂
H_a: p₁ ≠ p₂
The random variable is the difference between the proportions of Hispanic students at Cabrillo College and Lake Tahoe College.
normal for two proportions
test statistic: 4.29
p-value: 0.00002
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for decision: p-value < alpha
4. Conclusion: There is sufficient evidence to conclude that the proportions of Hispanic students at Cabrillo College and Lake Tahoe College are different.

104. p₂₀₁₁ ≤ p₂₀₁₀

106. Test: two independent sample proportions. Random variable: p′₁ – p′₂

Distribution:

H₀: p₁ = p₂
H_a: p₁ ≠ p₂

The proportion of eReader users is different for the 16- to 29-year-old users from that of the 30 and older users. Graph: two-tailed

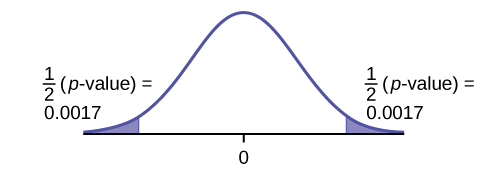
This is a normal distribution curve with mean equal to zero. Both the right and left tails of the curve are shaded. Each tail represents 1/2(p-value) = 0.0017.

p-value : 0.0033 Decision: Reject the null hypothesis. Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that the proportion of eReader users 16 to 29 years old is different from the proportion of eReader users 30 and older.

108. Test: two independent sample proportions Random variable: p′₁ − p′₂

Distribution:

H₀: p₁ = p₂
H_a: p₁ > p₂

A higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.

Graph: right-tailed

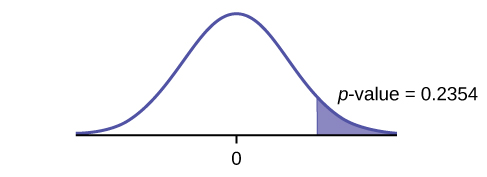
This is a normal distribution curve with mean equal to zero. A vertical line near the tail of the curve to the right of zero extends from the axis to the curve. The region under the curve to the right of the line is shaded representing p-value = 0.2354.

p-value: 0.2354 Decision: Do not reject the H₀. Conclusion: At the 1% level of significance, from the sample data, there is not sufficient evidence to conclude that a higher proportion of tablet owners are aged 16 to 29 years old than are 30 years old and older.

110. Subscripts: 1: men; 2: women

H₀: p₁ ≤ p₂
H_a: p₁ > p₂
P′1−P′2 is the difference between the proportions of men and women who enjoy shopping for electronic equipment.
normal for two proportions
test statistic: 0.22
p-value: 0.4133
Check student’s solution.
1. Alpha: 0.05
2. Decision: Do not reject the null hypothesis.
3. Reason for Decision: p-value > alpha
4. Conclusion: At the 5% significance level, there is insufficient evidence to conclude that the proportion of men who enjoy shopping for electronic equipment is more than the proportion of women.

112.

H₀: p₁ = p₂
H_a: p₁ ≠ p₂
P′1−P′2 is the difference between the proportions of men and women that have at least one pierced ear.
normal for two proportions
test statistic: –4.82
p-value: zero
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for Decision: p-value < alpha
4. Conclusion: At the 5% significance level, there is sufficient evidence to conclude that the proportion of males and females with at least one pierced ear is different.

114.

H₀: µ_d = 0
H_a: µ_d > 0
The random variable X_d is the mean difference in work times on days when eating breakfast and on days when not eating breakfast.
t₉
test statistic: 4.8963
p-value: 0.0004
Check student’s solution.
1. Alpha: 0.05
2. Decision: Reject the null hypothesis.
3. Reason for Decision: p-value < alpha
4. Conclusion: At the 5% level of significance, there is sufficient evidence to conclude that the mean difference in work times on days when eating breakfast and on days when not eating breakfast has increased.

Matched or Paired Samples – Homework

115. p-value = 0.1494 At the 5% significance level, there is insufficient evidence to conclude that the medication lowered cholesterol levels after 12 weeks.

117. There is sufficient evidence to conclude that the method reduces the proportion of HIV-positive patients who develop AIDS after four years.119. 0.0155; There is sufficient evidence to conclude that the blood pressure decreased after the training.121. Test: two matched pairs or paired samples (t-test) Random variable: [latex]\overline{X}_{d}[/latex] Distribution: t₁₂H₀: μ_d = 0 H_a: μ_d > 0 The mean of the differences of new female breast cancer cases in the south between 2013 and 2012 is greater than zero. The estimate for new female breast cancer cases in the south is higher in 2013 than in 2012.

Graph: right-tailed

p-value: 0.0004

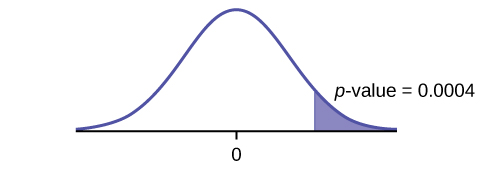
Decision: Reject H₀Conclusion: At the 5% level of significance, from the sample data, there is sufficient evidence to conclude that there was a higher estimate of new female breast cancer cases in 2013 than in 2012.

123. Test: matched or paired samples (t-test) Difference data: {–0.9, –3.7, –3.2, –0.5, 0.6, –1.9, –0.5, 0.2, 0.6, 0.4, 1.7, –2.4, 1.8} Random Variable:[latex]\overline{X}_{d}[/latex] Distribution: H₀: μ_d = 0 H_a: μ_d < 0 The mean of the differences of the rate of underemployment in the northeastern states between 2012 and 2011 is less than zero. The underemployment rate went down from 2011 to 2012.

Graph: left-tailed.

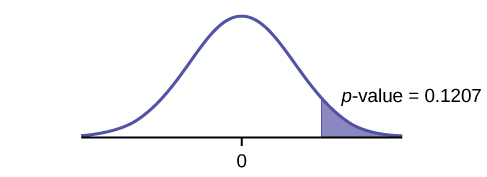
p-value: 0.1207 Decision: Do not reject H₀. Conclusion: At the 5% level of significance, from the sample data, there is not sufficient evidence to conclude that there was a decrease in the underemployment rates of the northeastern states from 2011 to 2012.

Bringing It Together: Homework

125. two proportions

127. single mean

129. single proportion

131. two proportions

133. single proportion

135. a test of two independent means.

Module 10: Hypothesis Testing With Two Samples