Graphing Linear Equations Using Ordered Pairs

Learning Outcomes

  • Complete a table of solutions for a linear equation
  • Graph linear equations using ordered pairs

By graphing ordered pairs, we can interpret mathematical relationships. You can use a coordinate plane to plot points and map various relationships, such as the relationship between an object’s distance and the elapsed time. Many mathematical relationships are linear relationships.

Plotting points to graph linear relationships

A linear relationship is a relationship between variables such that when plotted on a coordinate plane, the points lie on a line. Let’s start by looking at a series of points in Quadrant I on the coordinate plane.

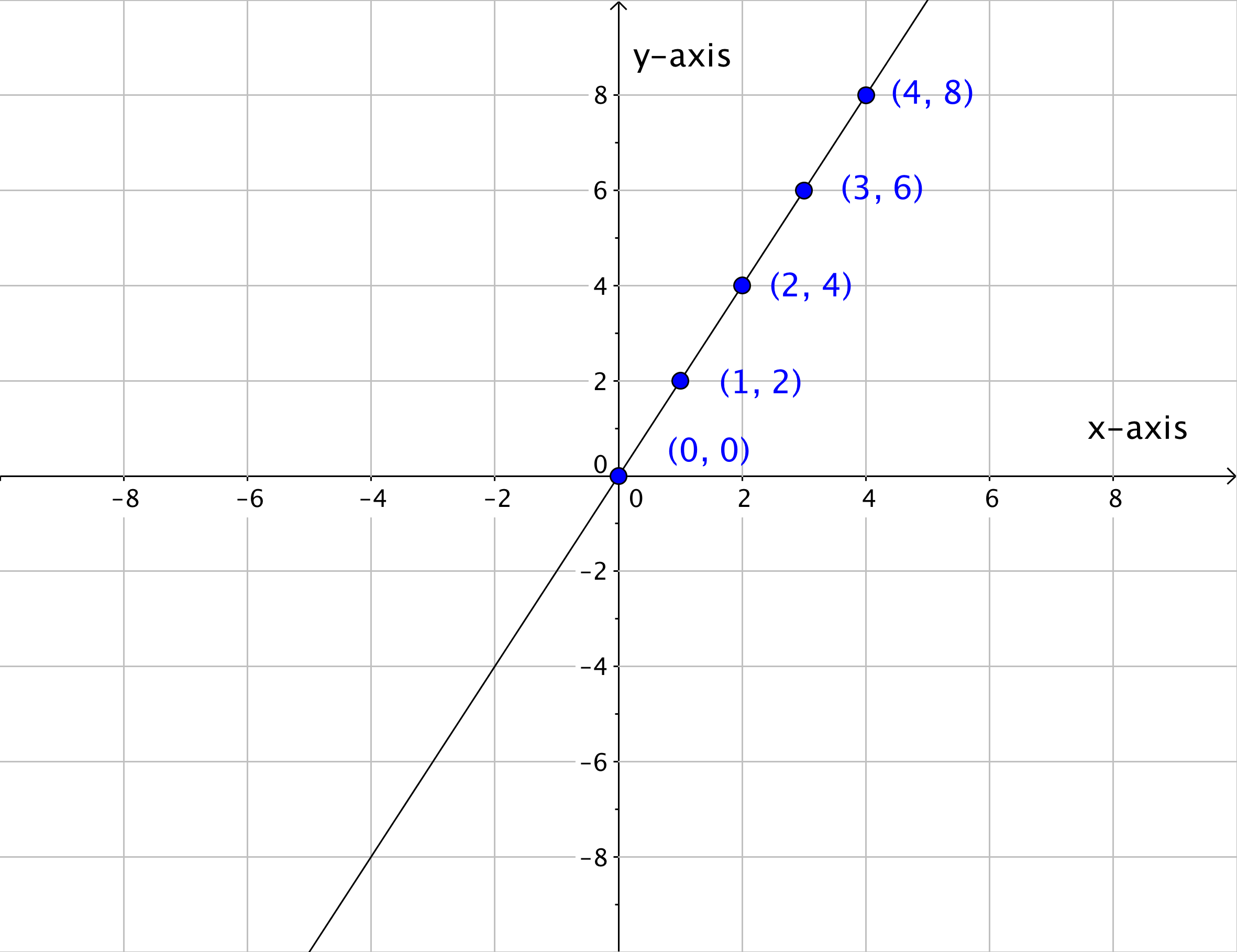
Look at the five ordered pairs (and their x– and y-coordinates) below. Do you see any pattern in the location of the points? If this pattern continued, what other points could be on the line?

You probably identified that if this pattern continued the next ordered pair would be at [latex](5, 10)[/latex]. This makes sense because the point [latex](5, 10)[/latex] “lines up” with the other points in the series—it is literally on the same line as the others. Applying the same logic, you may identify that the ordered pairs [latex](6, 12)[/latex] and [latex](7, 14)[/latex] would also belong if this coordinate plane were larger; they, too, will line up with the other points.

These series of points can also be represented in a table. In the table below, the x- and y-coordinates of each ordered pair on the graph is recorded.

x-coordinate y-coordinate
[latex]0[/latex] [latex]0[/latex]
[latex]1[/latex] [latex]2[/latex]
[latex]2[/latex] [latex]4[/latex]
[latex]3[/latex] [latex]6[/latex]
[latex]4[/latex] [latex]8[/latex]

Notice that each y-coordinate is twice the corresponding x-value. All of these x- and y-values follow the same pattern, and, when placed on a coordinate plane, they all line up.

Graph with the point (0,0); the point (1,2); the point (2,4); the point (3,6); and the point (4,8).

Once you know the pattern that relates the x- and y-values, you can find a y-value for any x-value that lies on the line. So if the rule of this pattern is that each y-coordinate is twice the corresponding x-value, then the ordered pairs [latex](1.5, 3), (2.5, 5)[/latex], and [latex](3.5, 7)[/latex] should all appear on the line too, correct? Look to see what happens.

Graph with the point (0,0); the point (1,2); the point (1.5, 3); the point (2,4); the point (2.5, 5); the point (3,6); the point (3.5, 7); and the point (4,8).

If you were to keep adding ordered pairs (x, y) where the y-value was twice the x-value, you would end up with a graph like this.

A line drawn through the point (0,0); the point (1,2); the point (2,4); the point (3,6); and the point (4,8).

Look at how all of the points blend together to create a line. You can think of a line, then, as a collection of an infinite number of individual points that share the same mathematical relationship. In this case, the relationship is that the y-value is twice the x-value.

There are multiple ways to represent a linear relationship—a table, a linear graph, and there is also a linear equation. A linear equation is an equation with two variables whose ordered pairs graph as a straight line.

There are several ways to create a graph from a linear equation. One way is to create a table of values for x and y, and then plot these ordered pairs on the coordinate plane. Two points are enough to determine a line. However, it’s always a good idea to plot more than two points to avoid possible errors.

Then you draw a line through the points to show all of the points that are on the line. The arrows at each end of the graph indicate that the line continues endlessly in both directions. Every point on this line is a solution to the linear equation.

Example

Graph the linear equation [latex]y=−1.5x[/latex].

Graph the linear equation

Example

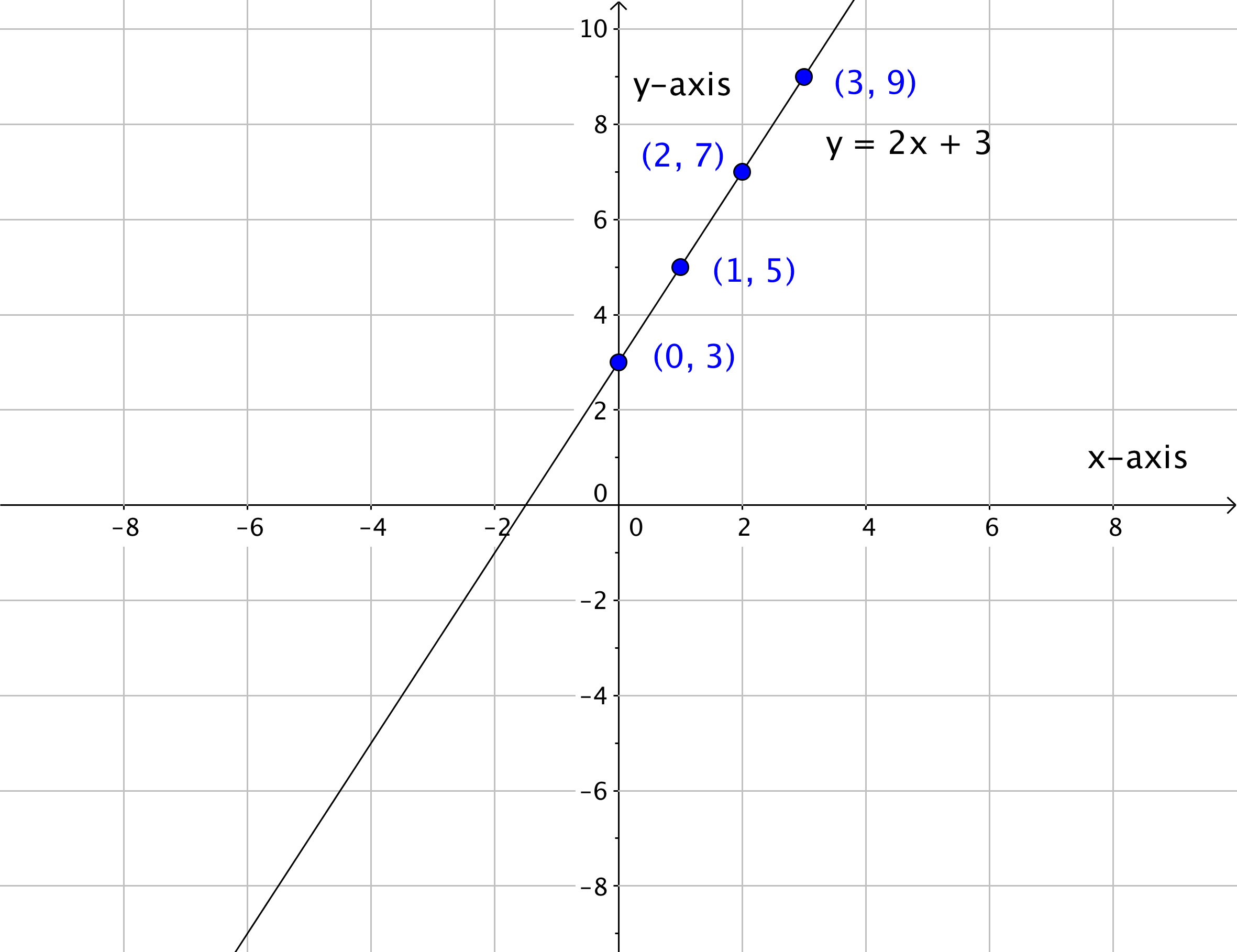
Graph the linear equation [latex]y=2x+3[/latex].

Try It