Logarithmic Functions

Learning Outcomes

  • Convert from logarithmic form to exponential form
  • Convert from exponential form to logarithmic form
  • Evaluate functions involving natural logarithms

In the graph of the exponential function [latex]y=10^{x}[/latex] shown below, we can see that every positive value of [latex]y[/latex] corresponds to exactly one value of [latex]x[/latex]. This is the one-to-one property of exponential functions. For any positive number [latex]b \neq 1[/latex]

[latex]b^{x}=b^{y}[/latex] if and only if [latex]x=y[/latex].

We may want to find what value of [latex]x[/latex] produces a value of [latex]y = 500[/latex]. We know that [latex]10^{2}=100[/latex] and [latex]10^{3}=1,000[/latex], so the correct value of [latex]x[/latex] is somewhere between [latex]2[/latex] and [latex]3[/latex].

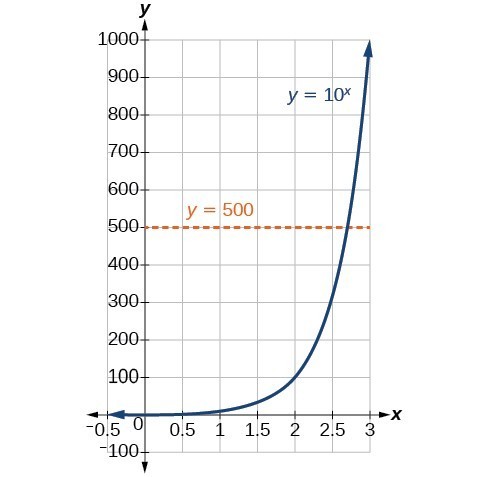
Graph of the intersections of the equations y=10^x and y=500.

Logarithmic functions are used to solve problems such as this.

We define the logarithmic function with base b as follows:

[latex]{\mathrm{log}}_{b}\left(x\right)=y\Leftrightarrow {b}^{y}=x,\text{}b>0,b\ne 1[/latex].
The two statements [latex]y=\mathrm{log}_{b} x[/latex] and [latex]b^{y}=x[/latex] are equivalent. We say that [latex]y=\mathrm{log}_{b} x[/latex] is the logarithmic form of [latex]b^{y}=x[/latex] is the exponential form.

Note that the base b is always positive.

The value [latex]x[/latex] in parentheses is called the argument. The argument is the quantity we are taking the logarithm of. Since [latex]b^{y}>0[/latex], and [latex]x=b^{y}[/latex], the argument of a logarithm must be positive.


Think b to the y equals x.

Example

Write the following logarithmic equations in exponential form.

  1. [latex]\mathrm{log}_{2} 8 =3[/latex]
  2. [latex]\mathrm{log}_{3} 9 =2[/latex]
  3. [latex]\mathrm{log}_{4} \frac{1}{16} =-2[/latex]

In the following video are more examples of rewriting logarithmic equations as exponential equations.

Convert from Exponential to Logarithmic Form

To convert from exponential form to logarithmic form, we follow the same steps in reverse. We identify the base b, exponent x, and output y. Then we write [latex]x={\mathrm{log}}_{b}\left(y\right)[/latex].

Example

Write the following exponential equations in logarithmic form.

  1. [latex]{2}^{3}=8[/latex]
  2. [latex]{5}^{2}=25[/latex]
  3. [latex]{10}^{-4}=\frac{1}{10,000}[/latex]

The next video shows more examples of writing exponential expressions in logarithmic form.

Many calculators can evaluate only two types of logarithmic functions.

Common logarithms, written [latex]\mathrm{log}(x)[/latex], have an implied base [latex]b=10[/latex].

[latex]\mathrm{log}(x) = \mathrm{log}_{10} (x)[/latex]

Natural logarithms, written [latex]\mathrm{ln}(x)[/latex], have base [latex]e[/latex].

[latex]\mathrm{ln}(x) = \mathrm{log}_{e} (x)[/latex]

We can use logarithms to solve exponential equations. That is, equations where the variable appears in an exponent.

Consider the example at the beginning of this section. We wanted to find the value of [latex]x[/latex] such that [latex]10^{x}=500[/latex]. If we rewrite this exponential expression in logarithmic form we have [latex]\mathrm{log}_{10} 500=x[/latex] or simply [latex]\mathrm{log} \ 500=x[/latex]. Using a calculator we can find an approximate value for [latex]x, x \approx 2.69897[/latex].

The most frequently used base for logarithms is [latex]e[/latex]. In the next example, we will evaluate a natural logarithm using a calculator.

Example

Evaluate [latex]y=\mathrm{ln}\left(500\right)[/latex] to four decimal places using a calculator.

In our next video, we show more examples of how to evaluate natural logarithms using a calculator.