Learning Outcomes
- Conduct a hypothesis test for matched or paired data and interpret the conclusion in context
When using a hypothesis test for matched or paired samples, the following characteristics should be present:
- Simple random sampling is used.
- Sample sizes are often small.
- Two measurements (samples) are drawn from the same pair of individuals or objects.
- Differences are calculated from the matched or paired samples.
- The differences form the sample that is used for the hypothesis test.
- Either the matched pairs have differences that come from a population that is normal or the number of differences is sufficiently large so that distribution of the sample mean of differences is approximately normal.
In a hypothesis test for matched or paired samples, subjects are matched in pairs, and differences are calculated. The differences are the data. The population mean for the differences, μd, is then tested using a Student’s t-test for a single population mean with n – 1 degrees of freedom, where n is the number of differences.
The test statistic (t-score) is:
[latex]\displaystyle{t}=\dfrac{{\overline{{x}}_{{d}}-{\mu}_{{d}}}}{{{(\dfrac{{s}_{{d}}}{\sqrt{{n}}})}}}[/latex]
Recall: ORDER OF OPERATIONS
| Please | Excuse | My | Dear | Aunt | Sally |
| parentheses | exponents | multiplication | division | addition | subtraction |
| [latex]( \ )[/latex] | [latex]x^2[/latex] | [latex]\times \ \mathrm{or} \ \div[/latex] | [latex]+ \ \mathrm{or} \ -[/latex] | ||
To calculate the test statistic (t-score) follow these steps:
First, find the numerator. Calculate the difference between the matched or paired sample mean and the population mean for the differences, [latex](\overline{x} _d - \mu _d)[/latex].
Second, find the denominator.
Step 1: Find the square root of the sample size (number of differences), [latex]\sqrt{n}[/latex].
Step 2: Take the population standard deviation for the differences and divide by the value you found in Step 1.
Third, take the numerator and divide by the denominator.
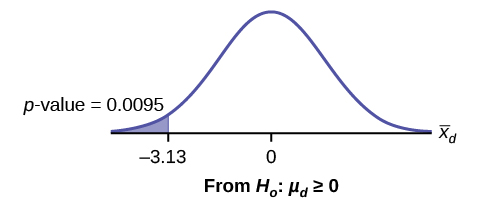
Example 1
A study was conducted to investigate the effectiveness of hypnotism in reducing pain. Results for randomly selected subjects are shown in the table below. A lower score indicates less pain. The “before” value is matched to an “after” value and the differences are calculated. The differences have a normal distribution. Are the sensory measurements, on average, lower after hypnotism? Test at a 5% significance level.
| Subject: | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Before | 6.6 | 6.5 | 9.0 | 10.3 | 11.3 | 8.1 | 6.3 | 11.6 |
| After | 6.8 | 2.4 | 7.4 | 8.5 | 8.1 | 6.1 | 3.4 | 2.0 |
Note
For the TI-83+ and TI-84 calculators, you can either calculate the differences ahead of time (after – before) and put the differences into a list or you can put the after data into a first list and the before data into a second list. Then, go to a third list and arrow up to the name. Enter 1st list name – 2nd list name. The calculator will do the subtraction, and you will have the differences in the third list.
USING THE TI-83, 83+, 84, 84+ CALCULATOR
- Use your list of differences as the data.
- Press
STATand arrow over toTESTS. - Press
2:T-Test. - Arrow over to
Dataand pressENTER. - Arrow down and enter
0for the name of the list where you put the data, and1for Freq:. - Arrow down to
μ: and arrow over to<. - Press
ENTER. - Arrow down to
Calculateand pressENTER. - The p-value is 0.0094, and the test statistic is –3.04.
- Do these instructions again except, arrow to
Draw(instead ofCalculate). PressENTER.
try it 1
A study was conducted to investigate how effective a new diet was in lowering cholesterol. Results for the randomly selected subjects are shown in the table. The differences have a normal distribution. Are the subjects’ cholesterol levels lower on average after the diet? Test at the 5% level.
| Subject | A | B | C | D | E | F | G | H | I |
| Before | 209 | 210 | 205 | 198 | 216 | 217 | 238 | 240 | 222 |
| After | 199 | 207 | 189 | 209 | 217 | 202 | 211 | 223 | 201 |
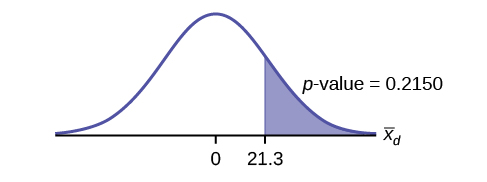
Example 2
A college football coach was interested in whether the college’s strength development class increased his players’ maximum lift (in pounds) on the bench press exercise. He asked four of his players to participate in a study. The amount of weight they could each lift was recorded before they took the strength development class. After completing the class, the amount of weight they could each lift was again measured. The data are as follows:
| Weight (in pounds) | Player 1 | Player 2 | Player 3 | Player 4 |
|---|---|---|---|---|
| Amount of weight lifted prior to the class | 205 | 241 | 338 | 368 |
| Amount of weight lifted after the class | 295 | 252 | 330 | 360 |
The coach wants to know if the strength development class makes his players stronger, on average.
try it 2
A new prep class was designed to improve SAT test scores. Five students were selected at random. Their scores on two practice exams were recorded, one before the class and one after. The data recorded in this table. Are the scores, on average, higher after the class? Test at a 5% level.
| SAT Scores | Student 1 | Student 2 | Student 3 | Student 4 |
|---|---|---|---|---|
| Score before class | 1840 | 1960 | 1920 | 2150 |
| Score after class | 1920 | 2160 | 2200 | 2100 |
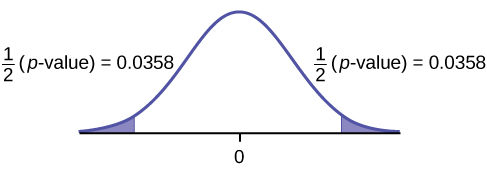
Example 3
Seven eighth-graders at Kennedy Middle School measured how far they could push the shot-put with their dominant (writing) hand and their weaker (non-writing) hand. They thought that they could push equal distances with either hand. The data were collected and recorded in this table.
| Distance (in feet) using | Student 1 | Student 2 | Student 3 | Student 4 | Student 5 | Student 6 | Student 7 |
|---|---|---|---|---|---|---|---|
| Dominant Hand | 30 | 26 | 34 | 17 | 19 | 26 | 20 |
| Weaker Hand | 28 | 14 | 27 | 18 | 17 | 26 | 16 |
Conduct a hypothesis test to determine whether the mean difference in distances between the children’s dominant versus weaker hands is significant.
try it 3
Five ball players think they can throw the same distance with their dominant hand (throwing) and off-hand (catching hand). The data were collected and recorded in the table below. Conduct a hypothesis test to determine whether the mean difference in distances between the dominant and off-hand is significant. Test at the 5% level.
| Player 1 | Player 2 | Player 3 | Player 4 | Player 5 | |
|---|---|---|---|---|---|
| Dominant Hand | 120 | 111 | 135 | 140 | 125 |
| Off-hand | 105 | 109 | 98 | 111 | 99 |
Candela Citations
- Statistics, Matched or Paired Sample. Provided by: OpenStax. Located at: https://openstax.org/books/statistics/pages/10-4-matched-or-paired-samples-optional. License: CC BY: Attribution. License Terms: Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Introductory Statistics. Authored by: Barbara Illowsky, Susan Dean. Provided by: OpenStax. Located at: https://openstax.org/books/introductory-statistics/pages/1-introduction. License: CC BY: Attribution. License Terms: Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction
- Z-statistics vs. T-statistics | Inferential statistics | Probability and Statistics | Khan Academy . Authored by: Khan Academy. Located at: https://www.youtube.com/embed/5ABpqVSx33I. License: All Rights Reserved. License Terms: Standard YouTube License